遠近法/いい加減に描く○点透視図 - KNDY

というわけで、ここでは厳密な幾何学的考察は一切せず、ややいい加減かつ自然に見えるな○点透視図を描いてみよう、と思う。まあ、線を引くわけですから物差しとコンパス、あと電卓(√計算が出来るもの)くらいは用意してくれたまえ。お絵かきソフトがあればPCで事足りるだろう。

実のところ、前回のように｢この軸をこの角度だけ傾けて･･･アオリ角度はこのくらいつけて･･･｣と厳密に考えさえしなければ、透視図における消失点の位置なんてのは、結構適当に決めてしまって問題ない。但し、自然な透視図に大切なのは｢一に中心点、二に画角｣である。適当に決めた消失点から、画面の中心点を見つけ出し、画角を適切に決めよう、というのが今回の趣旨だ。三角関数は使わないので心配は無用。

目次

---

いい加減に描く二点透視図

• まず適当に直線を一本引く。

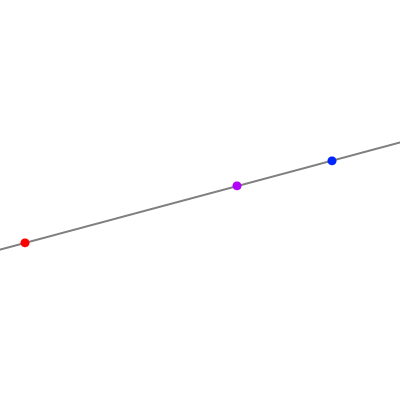
• 次に直線の上に適当に3つ点を打つ。

• 真ん中の点を中心点、あとの2つは消失点にする。(中心点決定)

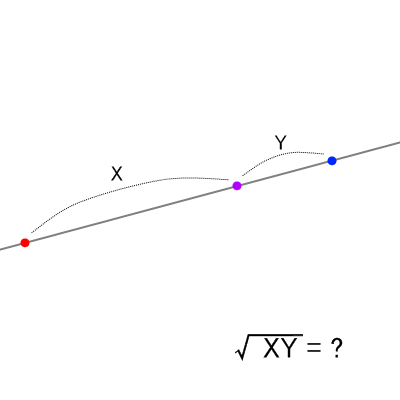
• 図中のXとYの長さを測ってを計算する。

• 半径の円が45°に相当する。

• 画角が大きくならないように気をつけてトリミングする。(画角決定)

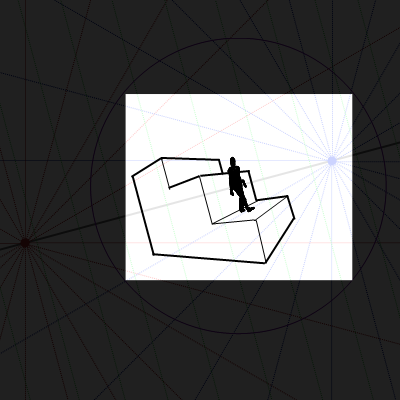
• おしまい。

ちなみに45°という画角(*1)はかなりの、いわゆるヒキの構図に相当する。ごく普通の構図にするなら15°くらいで十分だろう。というわけで、よりヨリの構図にするばあいにはに画角のタンジェントの値をかけてやればいい。

画角θ[゜]	45	40	35	30	25	20	15	10	5
tanθ	1	0.84	0.70	0.58	0.47	0.36	0.27	0.18	0.09

つまりほとんどの場合、消失点間の長さに対してトリミングされる領域なんてのはほんのわずか、猫の額なのである。

▲上へ

いい加減に描く三点透視図

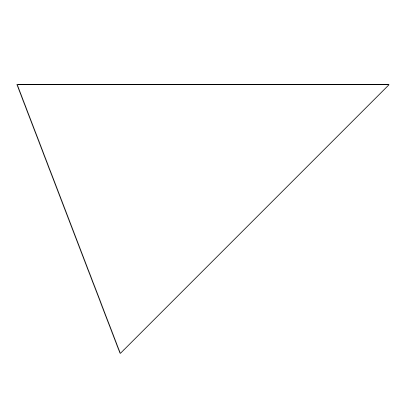
• まず三角形を描く。鋭角三角形(全ての角が90°未満であるような三角形)であれば、どんな三角形でもよい。三角形の頂点はそれぞれ消失点になる。

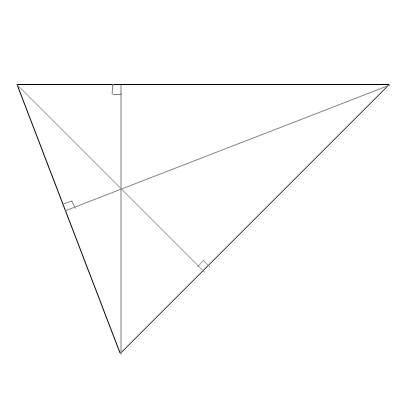
• 次に、各頂点から向かい合う辺に垂線を下ろす。すると3本の垂線は必ず一点で交わる(垂心という)。この交点が画面の中心点となる。(説明を分かりやすくするために垂線を3本引いたが、垂心を求めるだけであれば本来は2本でよい。)

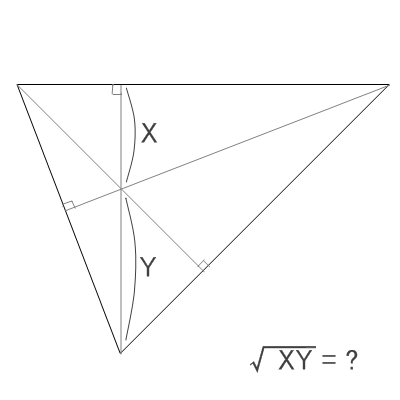
• 1本の垂線に沿って、辺から垂心までの距離X、および垂心から頂点までの距離Yを測り、例によってを計算する。(*2)

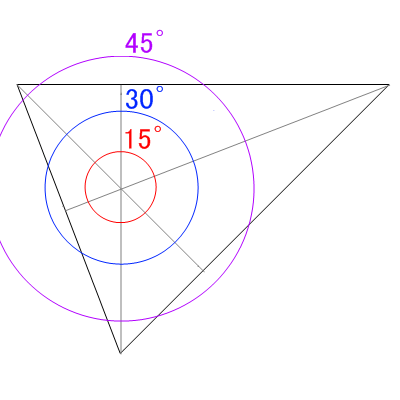
• 半径の円が、やっぱり45°に相当する。先ほど出てきた表を使って計算すれば、他の角度についても目安となる円が描ける。

• 例によって円の半径を目安に画面の大きさを決めて･･･(*3)

• できあがり。

ね？簡単でしょ？

▲上へ

電卓を使わない方法

｢なにとか云っちゃってんのマジウゼー｣という人向け。まあ、視野角45°というのはあくまで画角決定の目安だから、厳密に計算しなくても良いのだけどね。などの無理数であっても「あ、4より大きくて5より小さい位だな」くらいで十分に目安にはなるだろう。
それはともかく、これから説明するのはの円が定規コンパスのみで作図出来てしまう、という方法である。正直自分でもこの発見には驚いた(基礎的な幾何学の定理か何かには違いないのだろうが)。まるで、風呂桶にお湯を張ろうとしたら頭上からシャワーが降ってきた、そんな衝撃だった。
というわけで、早速やってみよう。

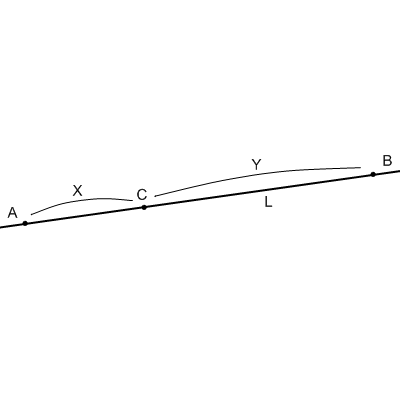
• 上での説明における、二点透視・三点透視どちらの場合でもいい。直線Lの上に点A,B,Cがあり、線分AC,線分CBの長さがそれぞれX,Yだったとする。

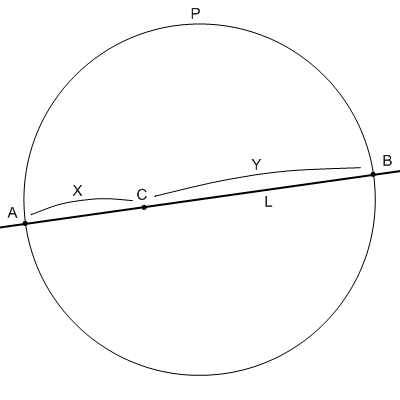
• 図中の線分ABを直径とするような円Pを描く。

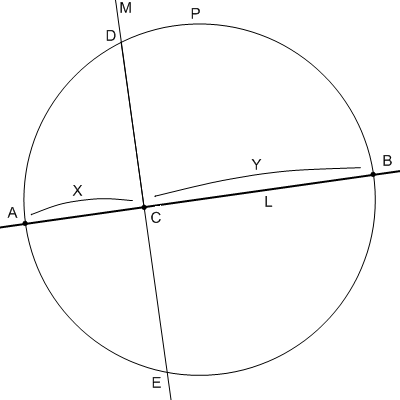
• Lに垂直でCを通るような直線Mを引き、円Pとの交点をD,Eとする。

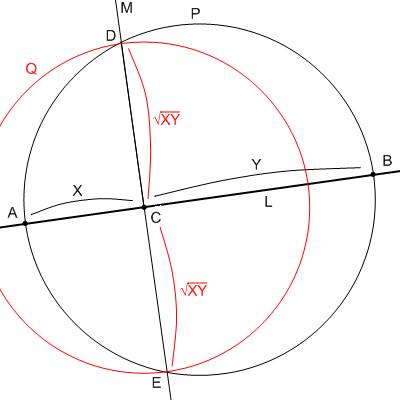
• すると、線分CDの長さ(=線分CEの長さ)はとなり、円Qが視野角45°を表す事になる。

計算か作図か、どちらのほうが手間がかかるかはその時々だろうが、少なくとも上の作図はフリーハンドで大まかに描けるので、構図を決める目安とするにはもってこいであろう。

▲上へ

（最終更新日：2011年08月25日）

&link_trackback(text=トラックバック表示)

• E点ってAとBから線を引くと常に90度じゃないですか？後このE点の直角を元に正方形を描きその対角線を水平線まで伸ばすと作図上の対角線の消失点が得られるってのは正しいのでしょうか。 -- ko (2011-08-24 00:53:18)
• ◯点透視図法では3次元直線は必ず直線として投影されることと、透視図法は局所的には平行投影になっていることを考えると、そのような結論になります。 -- KNDY (2011-08-25 07:26:00)