KNDY
市松模様を描いてみよう
最終更新:
Bot(ページ名リンク)
-
view
目次
とりあえず普通に市松模様を描く
「ちょっと待て!遠近法を使わないんだったら説明してくれなくたって描けるよ!おんなし正方形を並べりゃいいんだろう?」
― それはそうなのだが、遠近法の画面というのは角度や長さが歪んだ世界だから正確な長さが分かりにくい。正方形を描くためには何をしなけりゃならないのか、まずはそれを考えよう。
「簡単だよ、物差しがあるんだから、縦横の長さを測って・・・」
― じゃあその物差しに目盛りが無かったら・・・?
「え~、と。・・・フィーリング?スピリチュアルメッセージ?みたいな?」
― そんなもんで正確に描けるんだったら道理が引っ込む。三角関数まで持ち出して遠近法の説明した意味が無くなっちゃうよ。
― それはそうなのだが、遠近法の画面というのは角度や長さが歪んだ世界だから正確な長さが分かりにくい。正方形を描くためには何をしなけりゃならないのか、まずはそれを考えよう。
「簡単だよ、物差しがあるんだから、縦横の長さを測って・・・」
― じゃあその物差しに目盛りが無かったら・・・?
「え~、と。・・・フィーリング?スピリチュアルメッセージ?みたいな?」
― そんなもんで正確に描けるんだったら道理が引っ込む。三角関数まで持ち出して遠近法の説明した意味が無くなっちゃうよ。
正解は用紙の角を斜めに折る、だ。長方形のチラシで折り紙をした経験があるのではないだろうか。あとは詳しく述べずとも分かろうもの。
つまり、傾き0°,45°,90°の3種類の直線さえ正確に引ければ、正確な長さは分からずとも、同じ大きさの正方形を敷き詰めることが出来るのだ。
つまり、傾き0°,45°,90°の3種類の直線さえ正確に引ければ、正確な長さは分からずとも、同じ大きさの正方形を敷き詰めることが出来るのだ。

この考えを応用して、これから透視図中に市松模様を描いてみよう。すなわち、上の図で云うところの斜め45°の直線の消失点さえ見つけてやれば、手順は同じことだ。
二点透視図の市松模様(床編)
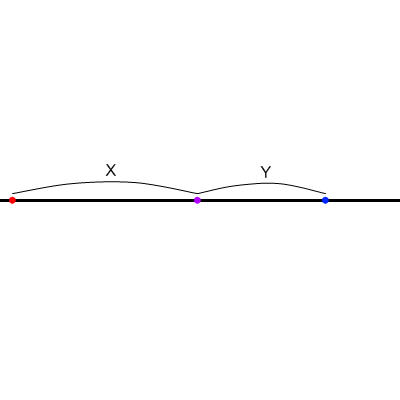
- 途中までは前回と同じように、消失点と中心点を決めてXとYの長さを測ろう。
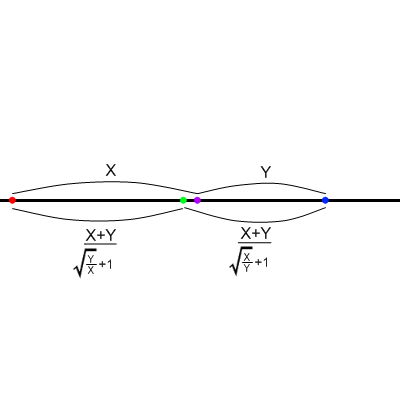
- 少々面倒な計算になるが、
または
の値を計算する。これが市松模様の対角線の消失点の位置を示す。
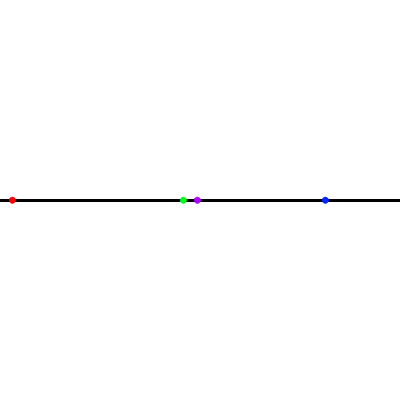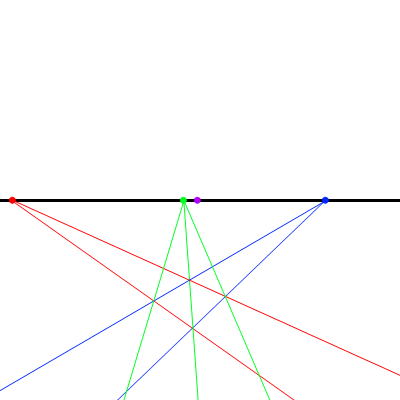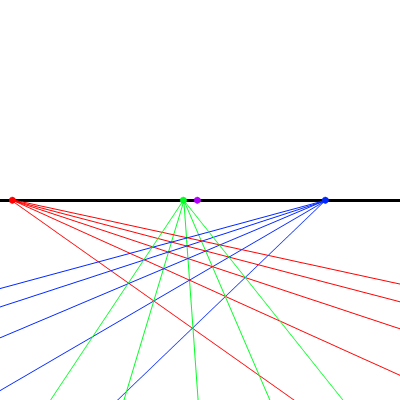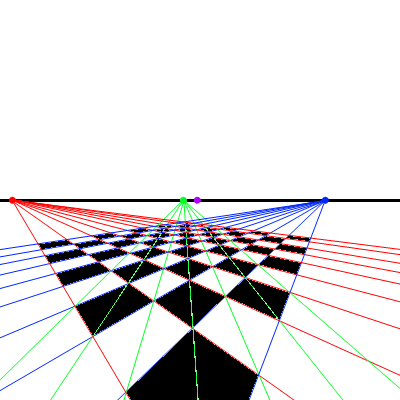
- あとは・・・できあがり。
さて、面倒なのは または
または の計算だが、実はこのよくわからん計算をせずとも、作図だけで対角線の消失点を見つける事が出来る。ホントだよ。
の計算だが、実はこのよくわからん計算をせずとも、作図だけで対角線の消失点を見つける事が出来る。ホントだよ。
以下のGIFアニメで示す。
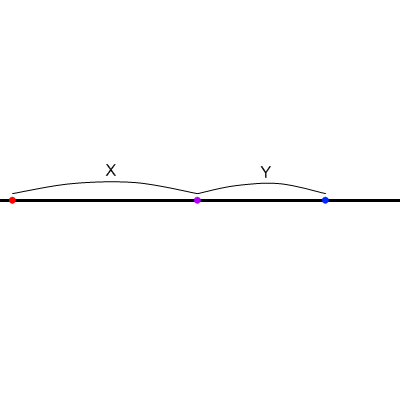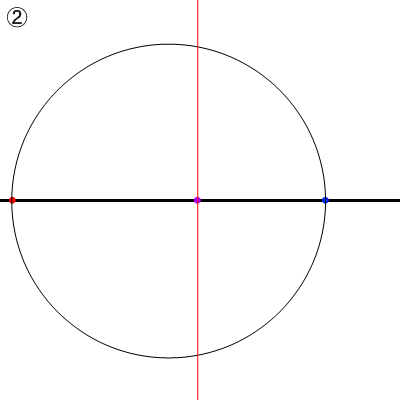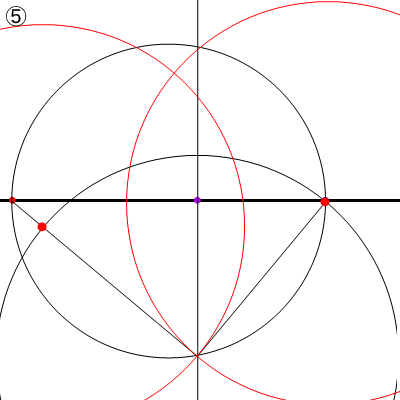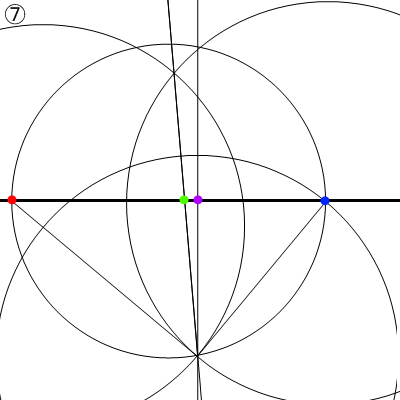
① 消失点間を直径とする円を描く
②③ 中心点を通る垂直線と円の交点を消失点と結び、直角三角形を作る。
③~⑥ 直角の二等分線を引く。
⑦ 角の二等分線と水平線の交点が、市松床の対角線の消失点となる。
以下のGIFアニメで示す。

① 消失点間を直径とする円を描く
②③ 中心点を通る垂直線と円の交点を消失点と結び、直角三角形を作る。
③~⑥ 直角の二等分線を引く。
⑦ 角の二等分線と水平線の交点が、市松床の対角線の消失点となる。
う~ん、手間でいうと数値計算といい勝負だな~。
二点透視図の市松模様(壁編)
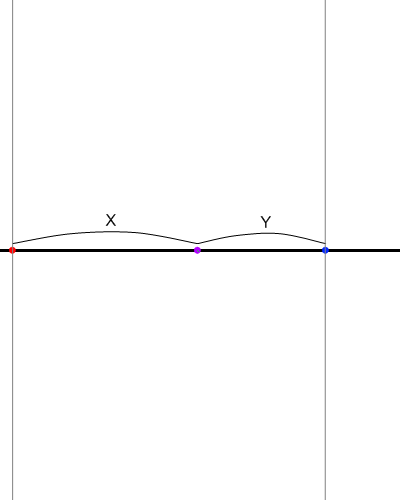
- 先程と同じ図を使おう。まず消失線を通るような鉛直線を引く。
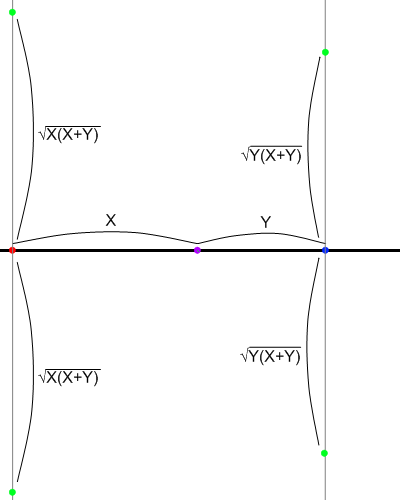
- 垂直線上に、消失点からそれぞれ
および
離れた位置に点を打つ。これらが壁に引かれた45°の平行線の消失点になる。対角線は2本引けるので、水平線の上下どちらの点も正方形の対角線群の消失点となる。
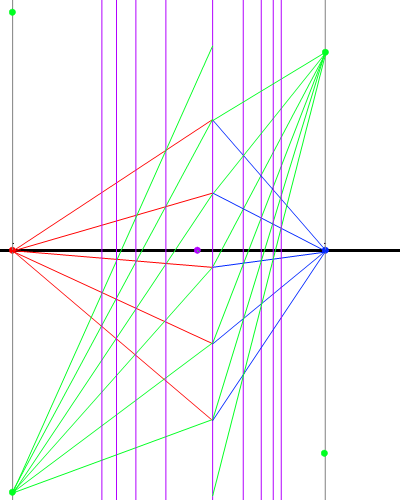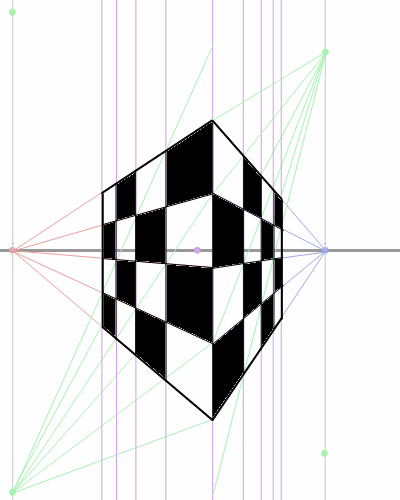
- 以上。(作例が歪んで見えるのは画角が異常に広いからだよ!トリミングは慎重かつ計画的に!)
それから例によって、 ,
, を計算せずに、消失点の位置を作図から求めてみよう。
を計算せずに、消失点の位置を作図から求めてみよう。
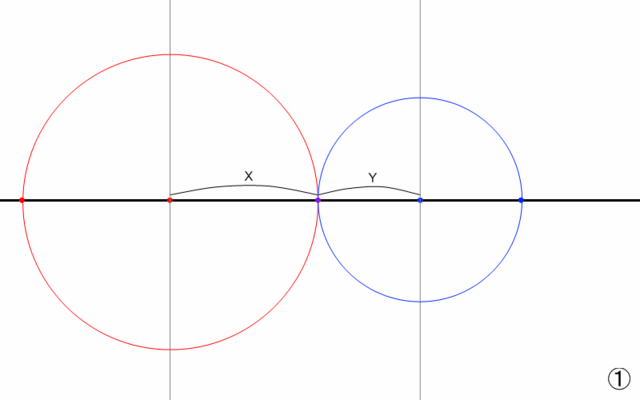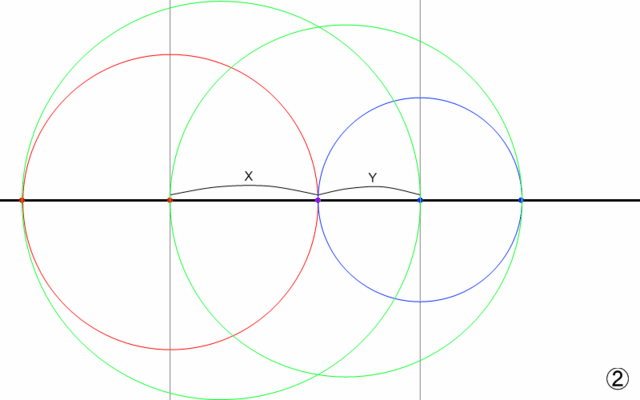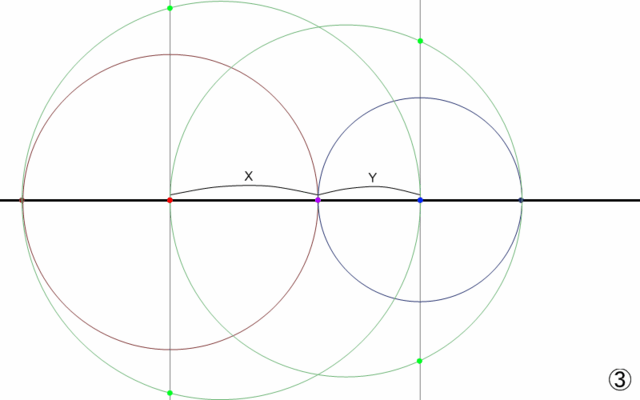
① それぞれの消失点から、さらにX,Yだけ中心から離れた水平線上の点を打つ。
② その点と、もう一方の消失点を直径とするような円を描く。
③ その円と、消失点を通る鉛直線との交点がくだんの消失点になる。

① それぞれの消失点から、さらにX,Yだけ中心から離れた水平線上の点を打つ。
② その点と、もう一方の消失点を直径とするような円を描く。
③ その円と、消失点を通る鉛直線との交点がくだんの消失点になる。
こっちは比較的簡単かも知れない。
三点透視図の市松模様
※三点透視では三軸について条件が対等なので、床・壁の区別は必要ない。
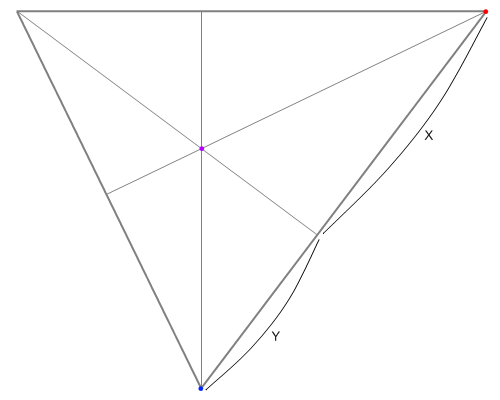

- 三角形を描いて垂線を下ろすところまでは前回と同じ。ただ、今回は三角形の辺の上の長さを測る。
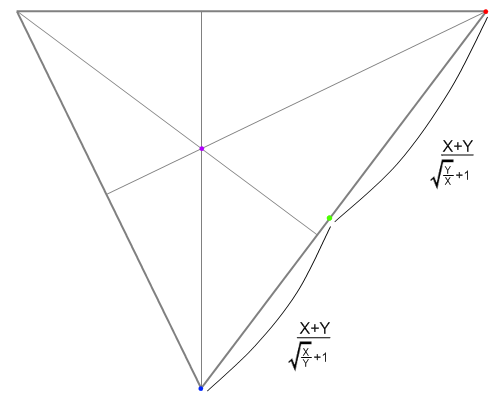
- あとはもう二点透視と一緒。
または
を計算して対角線の消失点を決める。
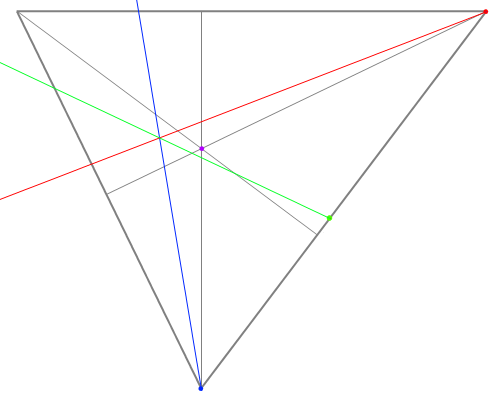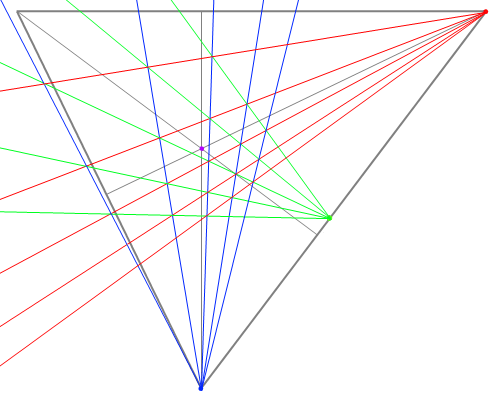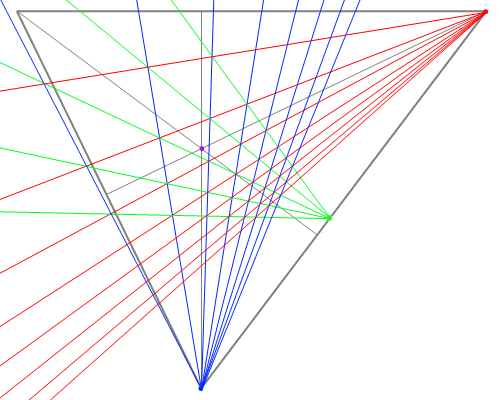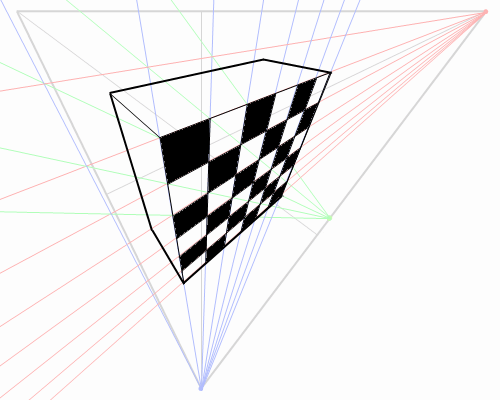
- おしまい。
お気づきのこととは思うが、 または
または を計算しなくとも、二点透視図の市松模様(床編)で説明したのと同様の作図方法で消失点を求める事が出来る。
を計算しなくとも、二点透視図の市松模様(床編)で説明したのと同様の作図方法で消失点を求める事が出来る。
▲上へ
(最終更新日:2009年07月20日)
(最終更新日:2009年07月20日)
&link_trackback(text=トラックバック表示)
- すきまのうめ方教えてください。 -- Y (2009-07-20 16:36:51)
