はじめに
回転を扱うプログラミングは、初めての人には少々敷居の高いものです。
何故なら回転は3Dグラフィックの知識がないと理解しにくく、例えばπ(パイ)とか三角関数のように、学校の数学で習うようなものではないからです。
まったく予備知識がない状態で回転の処理に取り組むのは、非常に難解なパズルに挑むのに似ています。
そう、例えばルービックキューブを独力で解ける人なら、回転プログラムも簡単に理解できるかもしれません(^^;
ある程度LSLを使いこなしている人であっても、
「回転だけは・・・」
苦手意識を持っている人も少なくないくらいです。
私が受ける質問の中でも、回転関連のものはかなり多いです。
何故なら回転は3Dグラフィックの知識がないと理解しにくく、例えばπ(パイ)とか三角関数のように、学校の数学で習うようなものではないからです。
まったく予備知識がない状態で回転の処理に取り組むのは、非常に難解なパズルに挑むのに似ています。
そう、例えばルービックキューブを独力で解ける人なら、回転プログラムも簡単に理解できるかもしれません(^^;
ある程度LSLを使いこなしている人であっても、
「回転だけは・・・」
苦手意識を持っている人も少なくないくらいです。
私が受ける質問の中でも、回転関連のものはかなり多いです。
そんなわけで、ハッキリ言って回転は難しいです(^^;
にもかかわらず回転を使わないといけない場面というのは非常に多いのです。
例えば単純なドアを作るのにも、回転は出てきます。
乗り物を作ろうと思ったら、回転は避けて通れません。
逆説的に言うなら、回転を使えないと、作れるものの幅がずいぶんと狭くなってしまうとも言えます。
にもかかわらず回転を使わないといけない場面というのは非常に多いのです。
例えば単純なドアを作るのにも、回転は出てきます。
乗り物を作ろうと思ったら、回転は避けて通れません。
逆説的に言うなら、回転を使えないと、作れるものの幅がずいぶんと狭くなってしまうとも言えます。
ここでは回転の基本的なところから少しずつ仕組みと理屈を解説しつつ、なるべく回転の苦手意識を克服できるような内容を書いていきたいと思います。
rotation型
SLにおいて回転を扱う際に避けて通れないのがrotation型です。
俗に回転値とか回転データとか言います。
正式には四元数(クォータニオン)という行列値のことです。
俗に回転値とか回転データとか言います。
正式には四元数(クォータニオン)という行列値のことです。
その名が示す通り、4つの値から成り立っています。
LSLにおいては、x、y、z、sの4つの小数値です。
最初の3つx、y、zはオブジェクトが向いている方向を示しています。
最後のsはオブジェクトが向いている方向の軸の周囲をどのくらい回転しているかを意味します。
ハッキリ言って、このx、y、z、sの4つの小数値を見て、オブジェクトがどんな風に回転しているのかを即座に理解できるツワモノはあんまりいません(^^;
LSLにおいては、x、y、z、sの4つの小数値です。
最初の3つx、y、zはオブジェクトが向いている方向を示しています。
最後のsはオブジェクトが向いている方向の軸の周囲をどのくらい回転しているかを意味します。
ハッキリ言って、このx、y、z、sの4つの小数値を見て、オブジェクトがどんな風に回転しているのかを即座に理解できるツワモノはあんまりいません(^^;
この四元数、ハミルトンというイギリスのおっさんが今から150年以上も前に発見したものなんですが、今でこそ3D計算には欠かせない理論になっているものの、当時はまったくもって意味不明、こんなの何の役に立つんだ状態で持て余されていたそうです。
そりゃあ150年前と言えば日本では江戸時代、ネズミ小僧がウロウロしてた頃ですから(^^;
3Dの回転計算なんて誰一人として妄想すらしてなかった時代でしょう。
そりゃあ150年前と言えば日本では江戸時代、ネズミ小僧がウロウロしてた頃ですから(^^;
3Dの回転計算なんて誰一人として妄想すらしてなかった時代でしょう。
ハミルトン自身も理論は確立したものの実用性が見出せず、散々に考え悩んだ挙句に最後はアル中になって野たれ死んでます。
四元数が有効に利用されるようになるのは現代に至ってから。
長い間報われなかった理論であります。
いやぁ、報われない壮絶な野たれ死には天才には付き物ですね。
四元数が有効に利用されるようになるのは現代に至ってから。
長い間報われなかった理論であります。
いやぁ、報われない壮絶な野たれ死には天才には付き物ですね。
それが今や3Dの回転計算には欠かせないのが四元数です。
世の中の3Dコンピュータグラフィックは四元数が無かったら実現できないと言っても過言ではありません。
もちろんセカンドライフも例外ではなく、ログインした瞬間から四元数の恩恵にあずかっていると言えます。
世の中の3Dコンピュータグラフィックは四元数が無かったら実現できないと言っても過言ではありません。
もちろんセカンドライフも例外ではなく、ログインした瞬間から四元数の恩恵にあずかっていると言えます。
アバターの向きを変えるにも四元数。
オブジェクトを回転させるにも四元数。
カメラを動かすのだって四元数を使っています。
オブジェクトを回転させるにも四元数。
カメラを動かすのだって四元数を使っています。
野たれ死んでしまったハミルトンに感謝しましょう。
プリムを回転させたときには、
「ありがとうハミルトン」
ぜひ心の中でそう祈りを捧げてください。
プリムを回転させたときには、
「ありがとうハミルトン」
ぜひ心の中でそう祈りを捧げてください。
vector型
しかし四元数は難解過ぎます。
なんたって天才ハミルトンが編み出した必殺技ですので、我々軟弱な一般人が習得するのは困難です。
なんたって天才ハミルトンが編み出した必殺技ですので、我々軟弱な一般人が習得するのは困難です。
通常、セカンドライフ内でプリムを回転させるとき、どんな風にするかと言うと、X、Y、Zの3つの軸の周囲を回しますよね。
X軸回りを90度。次にZ軸回りを45度・・・というように。
ビルドウインドウの回転の設定も、入力欄はX、Y、Zだけになっているはずです。
この方法のほうが、四元数よりも直観的にわかりやすいからです。
X軸回りを90度。次にZ軸回りを45度・・・というように。
ビルドウインドウの回転の設定も、入力欄はX、Y、Zだけになっているはずです。
この方法のほうが、四元数よりも直観的にわかりやすいからです。
LSLにおいてはこの方式の回転はvector型で扱われます。
実際、スクリプトコードの中で回転を扱う際には大抵vector型で回転量を指定します。
例えばオブジェクトが左に90度回るような処理を書いている場合は、
実際、スクリプトコードの中で回転を扱う際には大抵vector型で回転量を指定します。
例えばオブジェクトが左に90度回るような処理を書いている場合は、
vector rot = <0.0, 0.0, 90.0>;
こんなコードを書いたりします。
これなら「Z軸回り(垂直軸に対して)90度回転」と読み取るのは容易です。
これなら「Z軸回り(垂直軸に対して)90度回転」と読み取るのは容易です。
このようにvector型で表現する回転値のことを、オイラー表現、と呼ぶことがあります。
ハミルトンよりさらに遡ること半世紀、今から200年以上前の数学者オイラーにちなんだ呼び方です。
彼もまた天才の例にもれず、最後は失明しながら研究に取り組むという壮絶な生き様を見せ付けてくれています。
ハミルトンよりさらに遡ること半世紀、今から200年以上前の数学者オイラーにちなんだ呼び方です。
彼もまた天才の例にもれず、最後は失明しながら研究に取り組むという壮絶な生き様を見せ付けてくれています。
LSLの関数の名前に出てくるEulerの読み方が「オイラー」です。
間違っても「エウレアー」とか読んではいけません。オイラーさんに失礼です。
間違っても「エウレアー」とか読んではいけません。オイラーさんに失礼です。
さて。
X、Y、Zの3つの角度を使うオイラー表現。
オイラー表現はハミルトンの四元数よりも我々素人にはわかりやすいのは言うまでもないですが、何故に難解なrotation型が必要なのでしょうか。
X、Y、Zの3つの角度を使うオイラー表現。
オイラー表現はハミルトンの四元数よりも我々素人にはわかりやすいのは言うまでもないですが、何故に難解なrotation型が必要なのでしょうか。
実はオイラー表現には致命的な弱点があるためです。
その弱点はジンバルロックと言われますが、少々イメージがしにくいのでよりわかりやすい例を示しておきます。
その弱点はジンバルロックと言われますが、少々イメージがしにくいのでよりわかりやすい例を示しておきます。
vector rot = <90.0, 0.0, 90.0>;
上記のオイラー表現はどのような回転を意味するでしょうか。
X軸回りを90度、Z軸回りを90度ということですが・・・。
次の(A)と(B)のうち、正しいのはどちらだかわかりますか。
X軸回りを90度、Z軸回りを90度ということですが・・・。
次の(A)と(B)のうち、正しいのはどちらだかわかりますか。
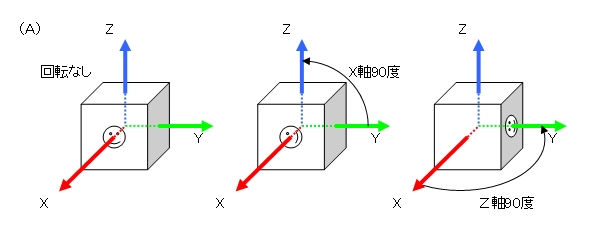
(A)はまずX軸の周囲を90度回転させ、それからZ軸の周囲を回転させています。
(B)はその逆に、Z軸、X軸の順で回転させています。
見てわかる通り、二つの方法はそれぞれ回転の結果が異なります。
(B)はその逆に、Z軸、X軸の順で回転させています。
見てわかる通り、二つの方法はそれぞれ回転の結果が異なります。
正解を言ってしまうと、セカンドライフにおける回転は(B)のほうになります。
オイラー表現による回転では、X、Y、Zのそれぞれの軸の回転順序が決まっていないと、どのように回転させるのが正しいのかが決まりません。
セカンドライフではZ、Y、Xの順に回転させる、と決まっているため(B)が正解ですが、他の3Dグラフィックも同じようになっているという保証はどこにもありません。
従ってvector型では厳密には回転を表現しきることが出来ないと言えます。
オイラー表現による回転では、X、Y、Zのそれぞれの軸の回転順序が決まっていないと、どのように回転させるのが正しいのかが決まりません。
セカンドライフではZ、Y、Xの順に回転させる、と決まっているため(B)が正解ですが、他の3Dグラフィックも同じようになっているという保証はどこにもありません。
従ってvector型では厳密には回転を表現しきることが出来ないと言えます。
厳密さを求めるのがコンピュータの世界ですので、オイラー表現よりも四元数のほうが都合が良いのです。
曖昧さを許す人間と機械との違いを浮き彫りにしているようで面白いところです。
曖昧さを許す人間と機械との違いを浮き彫りにしているようで面白いところです。
vectorとrotation間の変換
以上のように、回転を表現するデータにはrotationとvectorの二種類があり、そのどちらにもメリット・デメリットがあります。
rotationはコンピュータ向き、vectorは人間向き、とでも言うのが端的な説明かもしれません、
rotationはコンピュータ向き、vectorは人間向き、とでも言うのが端的な説明かもしれません、
この二種類のデータは、表現方法が異なるだけで回転の実態は一緒です。
例えば赤い果実のことを「りんご」と言うのと「アップル」と言うのとで、表現は違っても意味しているところのものは同一、というのと似ています。
例えば赤い果実のことを「りんご」と言うのと「アップル」と言うのとで、表現は違っても意味しているところのものは同一、というのと似ています。
LSLではvectorとrotationの回転を双方に翻訳するための関数が用意されています。
llEuler2Rot関数とllRot2Euler関数です。
この二つの関数を使って、vector表現の回転値とrotation型とは自由に変換が可能です。
llEuler2Rot関数とllRot2Euler関数です。
この二つの関数を使って、vector表現の回転値とrotation型とは自由に変換が可能です。
一般的な使い方としては、人間にわかりやすいvector型で回転値を定義し、実際に回転を行う前にllEuler2Rot関数でrotation型に変換する、というのが良くある手法です。
なお、llEuler2Rot関数で扱うことのできるvector型は、単位が度ではなくラジアンです。
ラジアンとは、円において弧の長さが半径と等しくなるような場合の中心角のことですが、言葉では何のことやらだと思うので図示してみました。
ラジアンとは、円において弧の長さが半径と等しくなるような場合の中心角のことですが、言葉では何のことやらだと思うので図示してみました。
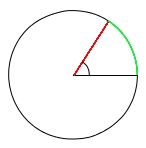
赤い線(半径)と緑の線(弧の長さ)が等しくなっています。
このときの2本の半径の間の角度が1ラジアンです。
このときの2本の半径の間の角度が1ラジアンです。
図から直観的にわかると思いますが、1ラジアンは180度の1/3に近いです。
正確には180度=πラジアンになります。
πは3.1415・・・ですから、ほぼ1/3というのは妥当な線でしょう。
ゆとり教育を実感できます。
正確には180度=πラジアンになります。
πは3.1415・・・ですから、ほぼ1/3というのは妥当な線でしょう。
ゆとり教育を実感できます。
逆に1度は何ラジアンかと言うと、π/180ですので、約0.0174533ラジアンということなります。
まぁ、LSLにおいてはそんなことは覚えておかなくても大丈夫です。
何故なら度数とラジアンを変換するのに便利な定数が用意されているためです。
何故なら度数とラジアンを変換するのに便利な定数が用意されているためです。
頻繁に使うのは度数からラジアンの変換だと思いますが、これにはDEG_TO_RADという定数を使います。
DEG_TO_RADの実態は先ほどの0.0174533です。
ですので例えば90度をラジアンに変換したい場合は、
DEG_TO_RADの実態は先ほどの0.0174533です。
ですので例えば90度をラジアンに変換したい場合は、
float rad = 90 * DEG_TO_RAD;
としてやれば良いことになります。
これを先ほどのオイラー:四元数変換と組み合わせて、
vector e_deg = <90, 0, 0>; // 度数のオイラー表現 vector e_rad = e_deg * DEG_TO_RAD; // ラジアンなオイラー表現 rotation rot = llEuler2Rot(e_rad); // 四元数
このように使います。
回転の向きについて
ログインして作業しているときは実際にオブジェクトの動きを目で見ながら確認できるのであまり意識しませんが、LSLのコードだけを無心に書いている時、
「はて、X軸の方向はどっちだったっけ?」
なんて迷いが生じることがあります。
ましてや回転の向きとなると、自分の望んでいる方向が+方向なのか-方向なのかわからなくなることもしばしば。
「はて、X軸の方向はどっちだったっけ?」
なんて迷いが生じることがあります。
ましてや回転の向きとなると、自分の望んでいる方向が+方向なのか-方向なのかわからなくなることもしばしば。
基礎知識として、セカンドライフの3D座標系について、向きの覚え方を書いておきます。
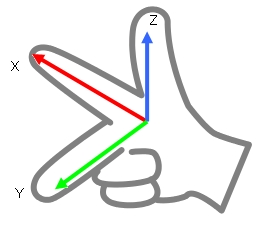
まず座標軸の方向ですが、いわゆる右手の法則で覚えます。
高校あたりで習う例のアレ、フレミングの法則と一緒ですので覚えやすいんじゃないでしょうか。
高校あたりで習う例のアレ、フレミングの法則と一緒ですので覚えやすいんじゃないでしょうか。
まず右手をピストルの形にします。
それから中指を人差し指と直角になる方向に伸ばす、と。
それから中指を人差し指と直角になる方向に伸ばす、と。
人差し指の向きがX方向、中指がY、親指がZになります。
さて、座標軸の方向がわかったところで、次に回転の向きですが、これまた右手を使います。
今度は親指を立て、残りの指をグーにした形です。
今度は親指を立て、残りの指をグーにした形です。
親指は回転の基準となる軸の+方向を示します。
残りの指の方向が、回転の+の向きです。
残りの指の方向が、回転の+の向きです。
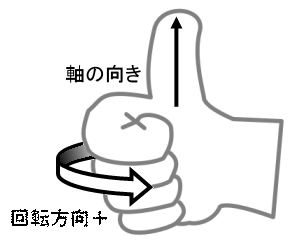
これはつまり、右ネジを締める方向が+ということです。
ネジを締めることの多い人なら、感覚的にわかるかもしれません。
ネジを締めることの多い人なら、感覚的にわかるかもしれません。
なお、人前で回転の向きを考える時は、決して親指を下向きにしてはいけません。
戦いになります。
戦いになります。
rotationの合成
実際に回転を処理し始めるとすぐにぶち当たる問題があります。
例えば金庫のダイヤル錠のように、
「右へ40度・・・次に左に65度・・・」
と回転させる動きを考えてみてください。
例えば金庫のダイヤル錠のように、
「右へ40度・・・次に左に65度・・・」
と回転させる動きを考えてみてください。
この動きを実現するには「ダイヤルの現在の角度」と「回す角度」を分けて考える必要があります。
何故ならLSLに用意されている回転関数は、基本的に全て「回転角度をXXにする」機能しかなく、「現在の角度からさらに動かす」機能はないからです。
つまり、ダイヤルを+40度動かすためには、オブジェクトの角度を「現在の角度+40度」に設定してやれば良いことになります。
何故ならLSLに用意されている回転関数は、基本的に全て「回転角度をXXにする」機能しかなく、「現在の角度からさらに動かす」機能はないからです。
つまり、ダイヤルを+40度動かすためには、オブジェクトの角度を「現在の角度+40度」に設定してやれば良いことになります。
しかしながら、ここで一つ注意しなければいけないことがあります。
rotation型のデータは、通常の方法(つまり+)では足し算できません。
同様に引き算(-)もできません。
これはもう決め事として覚えてしまったほうが早いことですが、rotation型の足し算では*(かける)を使い、引き算では/(わる)を使います。
rotation型のデータは、通常の方法(つまり+)では足し算できません。
同様に引き算(-)もできません。
これはもう決め事として覚えてしまったほうが早いことですが、rotation型の足し算では*(かける)を使い、引き算では/(わる)を使います。
何故そうなるのかは四元数理論の領域に踏み込んでしまうため割愛します。
いつかハミルトンと会うことがあったら尋ねてみて下さい。
いつかハミルトンと会うことがあったら尋ねてみて下さい。
従って、金庫のダイヤルを右へ40度回すには以下のようなコードになります。
rotation r1 = [[llGetRot]](); // 現在の角度 rotation r2 = llEuler2Rot(<40, 0, 0> * DEG_TO_RAD); // 40度(軸はX) llSetRot(r1 * r2); // 掛け算すると回転の合成になる
同様に、左へ65度回すコードです。
rotation r1 = llGetRot(); // 現在の角度 rotation r2 = llEuler2Rot(<65, 0, 0> * DEG_TO_RAD); // 65度(軸はX) llSetRot(r1 / r2); // 割り算すると逆回転の合成になる
回転の合成順序
合成には*と/を使いますが、さらに注意しなければいけないことがあります。
それは回転を合成するときの順序です。
それは回転を合成するときの順序です。
算数の世界では、掛け算の順序を入れ替えても答えは一緒になります。
2 * 5 = 10 5 * 2 = 10
しかし、回転の世界ではそうではありません。
具体的に考えてみましょう。
具体的に考えてみましょう。
あるオブジェクトの回転が、X軸周囲90度の状態だったとします。
llSetRot(llEuler2Rot(<90, 0, 0> * DEG_TO_RAD)); // X軸周囲を90度回転
このオブジェクトに対し、Z軸周囲90度の回転を加える場合どうなるでしょうか。
rotation r1 = llGetRot(); // 現在の角度(=X軸周囲90度回転) rotation r2 = llEuler2Rot(< 0, 0,90> * DEG_TO_RAD); // Z軸周囲を90度回転 llSetRot(r1 * r2);
この場合、まずr1回転が行われた後、r2回転をすることになります。
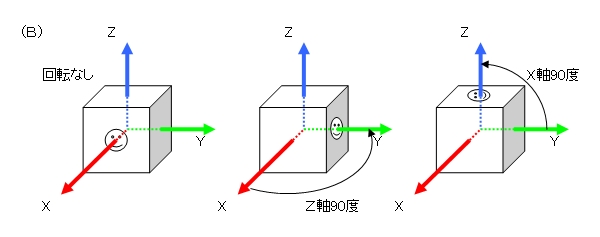
前にも出した図ですが、以下のようになります。
前にも出した図ですが、以下のようになります。

一方、r1とr2をかける順序を変えるとどうなるかと言うと、
rotation r1 = llGetRot(); // 現在の角度(=X軸周囲90度回転) rotation r2 = llEuler2Rot(< 0, 0,90> * DEG_TO_RAD); // Z軸周囲を90度回転 llSetRot(r2 * r1);
今度はまずr2回転が行われた後に、r1回転が行われます。

掛け算の順序を変えることで、回転の結果が変わってくるわけですが、これにはどんな意味があるのでしょうか。
グローバル座標系とローカル座標系
実は掛け算の順序を変えるということは、回転の基準となる軸を変えることと同じです。
3Dの座標系ではX,Y,Zとお馴染みの3つの軸があるわけですが、座標軸には基準によって種類があります。
3Dの座標系ではX,Y,Zとお馴染みの3つの軸があるわけですが、座標軸には基準によって種類があります。
最もイメージしやすいのはグローバル座標系です。
これはセカンドライフの全世界共通の座標軸で、X軸は西向き、Y軸は北向き、そしてZ軸は空を向いています。
ワールド座標系、とも言われますが、回転においては同一の意味です。
通常、セカンドライフでビルドを行う時、回転は全てグローバル座標を基準に指定します。
この座標系はオブジェクトがどのように回転しようとも、軸そものもが変化することはありません。
RLで喩えるなら、私が右を向こうが左を向こうが、はたまた逆立ちしようが、東は東ですし北は北です。
これがグローバル座標系です。
これはセカンドライフの全世界共通の座標軸で、X軸は西向き、Y軸は北向き、そしてZ軸は空を向いています。
ワールド座標系、とも言われますが、回転においては同一の意味です。
通常、セカンドライフでビルドを行う時、回転は全てグローバル座標を基準に指定します。
この座標系はオブジェクトがどのように回転しようとも、軸そものもが変化することはありません。
RLで喩えるなら、私が右を向こうが左を向こうが、はたまた逆立ちしようが、東は東ですし北は北です。
これがグローバル座標系です。
これに対してローカル座標系というものが存在します。
ローカル座標系はオブジェクト基準の座標系で、オブジェクト自体が回転すると向きが変わる座標系です。
人間で喩えるなら、ローカル座標系は前後・左右・頭足で表現される軸のことです。
私が向きを変えると、前方向は変化します。
寝転がったら頭の方向も変わりますよね。
セカンドライフのローカル座標系では、Xは前方向、Yは左方向、Zは頭の方向になっています。
これがローカル座標系です。
ローカル座標系はオブジェクト基準の座標系で、オブジェクト自体が回転すると向きが変わる座標系です。
人間で喩えるなら、ローカル座標系は前後・左右・頭足で表現される軸のことです。
私が向きを変えると、前方向は変化します。
寝転がったら頭の方向も変わりますよね。
セカンドライフのローカル座標系では、Xは前方向、Yは左方向、Zは頭の方向になっています。
これがローカル座標系です。
話を戻して、先ほどの回転に関して、グローバル座標軸とローカル座標軸がどのようになっているか見てみます。
まず、r2を適用する前のオブジェクトはX軸周囲を90度回転しています(下図の一番左の状態)。
まず、r2を適用する前のオブジェクトはX軸周囲を90度回転しています(下図の一番左の状態)。
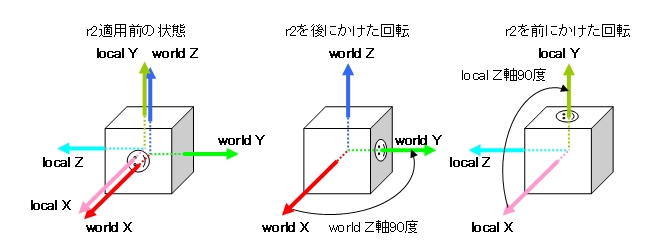
グローバル座標系はオブジェクトが回転しても向きが変わりません。
これに対してローカル座標系はオブジェクトの回転にあわせて向きが変わります。
ローカルのY軸とZ軸の向きが変わっていますね(ローカル座標軸は薄い色で示してあります)。
これに対してローカル座標系はオブジェクトの回転にあわせて向きが変わります。
ローカルのY軸とZ軸の向きが変わっていますね(ローカル座標軸は薄い色で示してあります)。
上図の真ん中は、r1 * r2の場合の回転です。
グローバルのZ軸に対して回転していることがわかります。
グローバルのZ軸に対して回転していることがわかります。
上図の一番右が、r2 * r1の場合です。
こちらはローカルのZ軸に対して回転していることになります。
こちらはローカルのZ軸に対して回転していることになります。
つまり話をまとめると、
あるオブジェクトの回転がr1のとき、 llSetRot(r1 * r2)はグローバル座標を基準としてオブジェクトを回転させる。 llSetRot(r2 * r1)はローカル座標を基準としてオブジェクトを回転させる。
ということになります。
これは回転を扱う際には重要な考え方です。
オブジェクトを回転させるとき、東西南北天地を基準としたいのか、それとも前後左右頭足を基準としたいのかで、計算式が変わるということになります。
オブジェクトを回転させるとき、東西南北天地を基準としたいのか、それとも前後左右頭足を基準としたいのかで、計算式が変わるということになります。
リンクプリムの回転
段々とややこしい世界に突入していきたいと思います(^^;
SLのオブジェクトは複数のprimで構成することが出来ますが、オブジェクトの中核となるprimのことをルートprimと呼び、その他のprimのことを子primとかリンクprimなどと表現するのは、今更説明するまでもないですよね。
ここまでの説明は基本的にオブジェクト全体、またはルートprimについてのお話でした。
今度は一歩踏み込んで、リンクprimの回転について考えてみます。
SLのオブジェクトは複数のprimで構成することが出来ますが、オブジェクトの中核となるprimのことをルートprimと呼び、その他のprimのことを子primとかリンクprimなどと表現するのは、今更説明するまでもないですよね。
ここまでの説明は基本的にオブジェクト全体、またはルートprimについてのお話でした。
今度は一歩踏み込んで、リンクprimの回転について考えてみます。
まずリンクprimの回転についての基本的な考え方ですが、リンクprimはルートprimからの相対的な回転で管理されます。
例えば、ルートprimに対してX軸周囲に90度回転した状態でリンクされているリンクprimがあるとします。
例えば、ルートprimに対してX軸周囲に90度回転した状態でリンクされているリンクprimがあるとします。
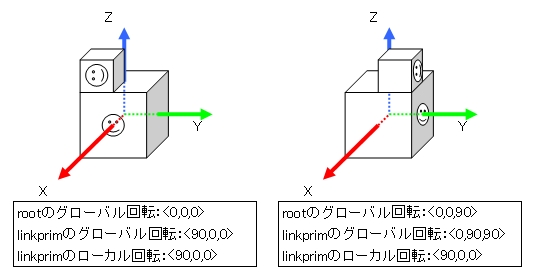
上図左側はルートの回転が0の場合です。
リンクprimはルートの回転に対してX軸周囲90度になっています。
リンクprimはルートの回転に対してX軸周囲90度になっています。
このオブジェクト全体をZ軸周囲90度回転させたのが右側の図です。
ルートの回転はZ軸周囲90度になっています。
リンクprimのグローバル軸に対する回転は<0,90,90>ですが、ルートprimに対する回転は<90,0,0>で変化なしです。
ルートの回転はZ軸周囲90度になっています。
リンクprimのグローバル軸に対する回転は<0,90,90>ですが、ルートprimに対する回転は<90,0,0>で変化なしです。
リンクprimのルートprimに対する回転のことを「ローカル回転」と呼びます。
前節で説明した通り、オブジェクトの軸のことを「ローカル軸」と言いますので、「ローカル軸」を基準とした回転のことを「ローカル回転」と表現するんですね。
前節で説明した通り、オブジェクトの軸のことを「ローカル軸」と言いますので、「ローカル軸」を基準とした回転のことを「ローカル回転」と表現するんですね。
LSLではローカル回転を扱う関数が用意されています。
rotation [[llGetLocalRot]]() // ローカル回転の取得 llSetLocalRot(rotation rot) // ローカル回転の設定
この二つの関数は、スクリプトが格納されているprimのローカル回転を取得/設定します。
つまり先ほどの図の例で言うと、小さなリンクprimにスクリプトを格納し、その中でllGetLocalRot関数を実行すると、X軸周囲90度回転のrotation値が取得できるということになります。
つまり先ほどの図の例で言うと、小さなリンクprimにスクリプトを格納し、その中でllGetLocalRot関数を実行すると、X軸周囲90度回転のrotation値が取得できるということになります。
llSetLocalRot?関数のほうはprimのローカル回転角度を設定する関数ですが、llSetRot?関数と同様、「primのローカル回転角度をXXXにする」働きがあります。
「現在のローカル回転角度からさらに動かす」わけではありませんので注意して下さい。
「現在のローカル回転角度からさらに動かす」わけではありませんので注意して下さい。
「現在のローカル回転角度からさらに動かす」ようにしたい場合は、「現在の角度」と「新たに動かしたい角度」を組み合わせて指定しなければいけません。
ということは、llSetRot?関数の時とまったく同じ問題が起きるということです。
掛け算の順序によって、回転の基準軸が変わる問題です。
ということは、llSetRot?関数の時とまったく同じ問題が起きるということです。
掛け算の順序によって、回転の基準軸が変わる問題です。
llSetRot?関数では、
llSetRot(現在角度 * 追加角度)はグローバル座標を基準としてオブジェクトを回転させる。 llSetRot(追加角度 * 現在角度)はローカル座標を基準としてオブジェクトを回転させる。
このような動きでした。
llSetLocalRot?関数ではどうなるのか、具体的に見てみます。
あるリンクprimがローカル回転<0,0,90>でルートprimにリンクされているとします。
あるリンクprimがローカル回転<0,0,90>でルートprimにリンクされているとします。
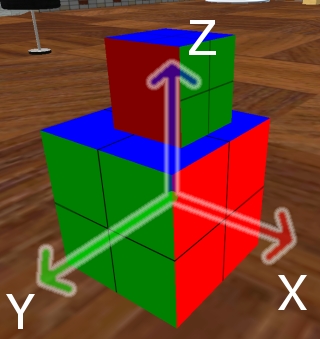
リンクprimの赤・緑の面がルートprimとはズレています。
ルートprimのZ軸を基準として90度回転していますので、リンクprimのX面は画像の右奥方向になっています。
このリンクprimに対して、さらにX軸基準に90度回転する処理を行います。
ルートprimのZ軸を基準として90度回転していますので、リンクprimのX面は画像の右奥方向になっています。
このリンクprimに対して、さらにX軸基準に90度回転する処理を行います。
まずは以下のように「現在角度x追加角度」で処理を行った場合です。
rotation r1 = llGetLocalRot(); // 現在のローカル角度(=Z軸周囲90度回転) rotation r2 = llEuler2Rot(<45, 0, 0> * DEG_TO_RAD); // X軸周囲を45度回転 llSetLocalRot(r1 * r2); // 現在角度x追加角度

ルートprimのX軸(赤い面)に対して回転していることがわかります。
これはつまりローカル軸基準の回転ということです。
これはつまりローカル軸基準の回転ということです。
次に掛け算の順序を変えて、「追加角度x現在角度」で処理を行います。
rotation r1 = llGetLocalRot(); // 現在のローカル角度(=Z軸周囲90度回転) rotation r2 = llEuler2Rot(<45, 0, 0> * DEG_TO_RAD); // X軸周囲を45度回転 llSetLocalRot(r2 * r1); // 追加角度x現在角度

今度はリンクprimのX軸(赤い面)に対して回転しています。
llSetRot?関数のときと同じような動きですが、基準となる軸が違うことに注意して下さい。
llSetLocalRot?関数を使った「追加角度x現在角度」は、リンクprim自身の軸を基準とした回転です。
llSetRot?関数のときと同じような動きですが、基準となる軸が違うことに注意して下さい。
llSetLocalRot?関数を使った「追加角度x現在角度」は、リンクprim自身の軸を基準とした回転です。
まとめると、リンクprimに対するllSetLocalRot?関数は、
llSetLocalRot(現在角度 * 追加角度)はルートprimのローカル軸を基準としてオブジェクトを回転させる。 llSetLocalRot(追加角度 * 現在角度)はリンクprimのローカル軸を基準としてオブジェクトを回転させる。
使い方を間違うと思いもよらない回転になりますので覚えておきましょう。
ところで、llGetLocalRot関数やllSetLocalRot?関数をルートprimに対して使った場合はどうなるでしょうか。
llGetLocalRot関数が「ローカル軸に対する回転を取得」する関数だということを考えると、ルートprimに対するllGetLocalRot関数は常に<0,0,0>を返してくれるのが筋のように思えます。
しかしながら、ルートprimに対してllGetLocalRot関数を実行した時は、例外的にグローバル回転角度が返ります。
同様に、llSetLocalRot?関数をルートprimに対して使った場合はグローバル回転角度の設定になります。
llGetLocalRot関数が「ローカル軸に対する回転を取得」する関数だということを考えると、ルートprimに対するllGetLocalRot関数は常に<0,0,0>を返してくれるのが筋のように思えます。
しかしながら、ルートprimに対してllGetLocalRot関数を実行した時は、例外的にグローバル回転角度が返ります。
同様に、llSetLocalRot?関数をルートprimに対して使った場合はグローバル回転角度の設定になります。
ということは言い換えるなら、
llGetLocalRot関数は、primの親軸(ルートならグローバル軸、リンクならルートの軸)基準の回転を返す llSetLocalRot関数は、primの親軸(ルートならグローバル軸、リンクならルートの軸)基準の回転を設定する
と言えます。
さて。
この時点ですでにだいぶややこしくなってきていますが、まだまだややこしい世界には先があります(^^;
お楽しみにw
この時点ですでにだいぶややこしくなってきていますが、まだまだややこしい世界には先があります(^^;
お楽しみにw
(つづく)
- 移動速度を検出して回転速度を変化させるスクリプトを作ったのですが、前進時の回転までしかできませんでした>w<;;; -- Backard Wylie (2008-04-23 14:30:33)
- エンターキー押しちゃったw ので、、、書き直し^^; default&173;state_entry()&173;llSetTimerEvent(0.20);&175;timer()&173;vector vel = llGetVel();float speed = llVecMag(vel);llTargetOmega(<1.0,0.0,0.0>,speed,1);&175; これを元に前進時の回転と行進時の回転を検出して自動で回転方向を切り替えてくれるスクリプトって作れるのかな~? -- Backard Wylie (2008-04-23 14:34:32)
- 文字化けしてますね^^; 消しといて下さい>w<;;; LsL-BBSに投稿したので、そちらで>< -- Backard Wylie (2008-04-23 14:37:02)
- こんなに決まり事があったのですね・・・わかりやすく説明されているので助かります。 -- くるじん (2008-11-07 18:48:39)
- ついに次回はベクトルの回転と四元数の使い方になるわけですねw -- 回転の国の王子様 (2009-03-27 10:58:03)
- いつも、わかり易い解説有難うございます。非常に参考になっています。 ところで、「BlackSheep-LSL@Wiki 回転について」のページについてですが、「グローバル座標系とローカル座標系」のところの、 > これはセカンドライフの全世界共通の座標軸で、X軸は西向き、Y軸は北向き、そしてZ軸は空を向いています。 のところの、「X軸は西向き」 ---> 「X軸は東向き」ではないでしょうか。 -- Xpyoda Janus (2019-02-16 11:41:30)
