相加相乗平均を攻略するZOY！ - OMC攻略wiki(非公式)

はじめに

　相加相乗平均の不等式を使いこなせる人ってかっこいいですよね！(ね！)
　特に, これは不等式の中でも基礎の不等式なので, 不等式分野をこれから学ぶ人はまず相加相乗平均の不等式を抑えておきましょう！

相加相乗平均の不等式ってな～に

　相加相乗平均の不等式とは次のような不等式です.

証明1

証明1
e^xを用いる方法.
以下のサイトの｢相加相乗平均の不等式の証明(n変数)｣を参照.
https://manabitimes.jp/math/566

証明2

証明2
双方向帰納法を用いる方法.

　step1. nが2べきのとき成り立つことを示す.
n=2のとき, (左辺)-(右辺)=1/2×(√a₁-√a₂)²≧0 より.
n=2^k(kは正の整数)で成り立つと仮定する.
a_l(1≦l≦n)=1/2×(b_2l-1+b_2l) を代入すると, n=2の不等式とあわせて, 2n=2^(k+1)のときも示されている.
よって, nが2べきのときは成り立つことが示された.
　step2. あるnで成り立つならn-1でも成り立つことを示す.
n=kで成り立つと仮定する.
a_k=1/(k-1)×(a₁+a₂+...+a_k-1) を代入すると次を得る.
　1/(k-1)×(a₁+a₂+...+a_k-1)≧ _k√{a₁a₂...a_k-1×1/(k-1)×(a₁+a₂+...+a_k-1)}
両辺をk乗→両辺を1/(k-1)×a₁+a₂+...+a_k-1で割る→両辺のk-1乗根をとる　よりn=k-1のときも成り立つ.
　よって帰納法が完成し, 全てのnについて示された.
(a₁ = a₂ = ... = a_n が等号成立条件なのは明らか. )

　正の実数でないと使えないことに注意して下さい.　実際, (-4)+(-8)/2 < 2√(-4)×(-8) となってしまいます.

使用例

　いきなりですが, 次のような問題を考えてみて下さい. 実はこれは相加相乗平均の不等式を使うことで解くことができます.

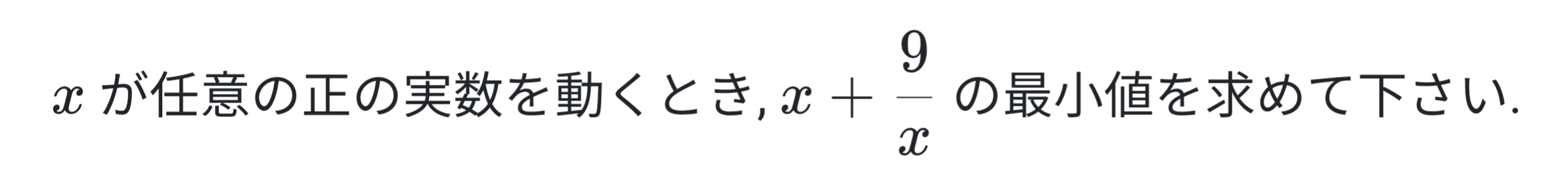
解答

解答
相加相乗平均の不等式より,
x+9/x ≧ 2√{x × 9/x} = 6.
x=3 のとき等号が成立するため, 答えは6.

等号成立条件の確認を忘れないようにしましょう.
このような問題では, 積が定数になることが重要です.

次数を合わせる

　さて, 数オリ・OMCでは次のような問題も頻出です. これは知らないと少し厳しいかもしれません.

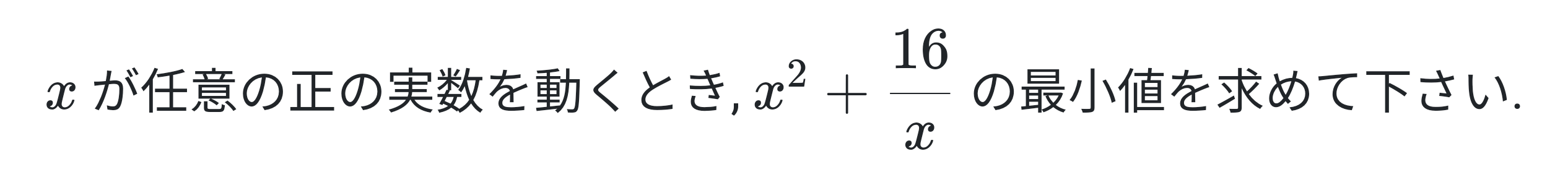
解答

解答
相加相乗平均の不等式より，
x²+16/x = x²+8/x+8/x ≧ 3 ³√{x² × 8/x × 8/x} = 12.
x=2 のとき等号が成立するため, 答えは12.

この問題では積が定数にならず, 2変数の相加相乗平均の不等式が上手く使えません．
そこで，解答では｢次数を合わせる｣ということを行っています．積がちゃんと定数になるのがミソです．

一般に, ax^m + bx^{-n} (x > 0) の最小値はこのように求めることができます.
(重み付き相加相乗? 聞いたことない名前ですね...)

重み付き相加相乗平均の不等式

　上でもちょっと触れましたが, 実はこんな不等式が成り立ちます．

証明

f(x)= -log x は凸関数であるから，これにJensenの不等式を適用する．
(Jensenの不等式については，今後執筆予定)

　式はごついですが, やっていることは｢次数を合わせる｣です．これを使うと上の問題を自然に解くことができます．

解答

解答
重み付き相加相乗平均の不等式より，
x²+16/x = 3/2 (1/3×2x² + 2/3×16/x) ≧ 3/2 × ³√(2x² × 256/x^2) = 12
x=2 のとき等号が成立するため, 答えは12.

　重みの和を1にしています．少なくとも筆者はこれが簡単だとは思いませんが...

problems

　中には難しいものもあるかもしれませんが，根気強く考えてみて下さい！ (概ね難易度順です.)

1.

　xが任意の正の実数を動くとき，x³+12/x の最小値を求めよ．

解答

解答
　相加相乗平均の不等式より，
x³+12/x = x³+4/x+4/x+4/x ≧ 4 ⁴√{x³ × 4/x × 4/x × 4/x} = 8√2.
x=√2 において等号成立．

2. (OMC136 - A)

　面積が 1000 である長方形について，周長のとり得る最小の整数値を求めてください．

解答

解答 (OMCのページ)
https://onlinemathcontest.com/contests/omc136/editorial/3295

3. (OMC143 - A)

　xが任意の正の実数を動くとき，(x + 20/x)(x + 500/x) の最小値を求めて下さい．

ヒント

ヒント
()それぞれに使うことはできない．(等号成立がx=√20=√500というおかしなことになってしまう！)
展開してみよう．

解答

解答 (OMCのページ)
https://onlinemathcontest.com/contests/omc143/editorial/5549
(このように，展開すると相加相乗平均の不等式が使えることがある．)

4.

　xが任意の正の実数を動くとき，x + 16/(x+1) の最小値を求めて下さい．

ヒント

ヒント
積を無理やり定数にする．

解答

解答
　相加相乗平均の不等式より，
x+1+16/(x+1) ≧ 2√16 = 8
であるから，求める答は 8-1 = 7.
x=3 において等号成立．

5. (OMC138 - D)

　正整数 n について，n²/5 + 200/n のとりうる最小値を求めてください．

ヒント

ヒント
等号成立条件を満たすnは整数にならない．周辺の正整数を調べよう．

解答

解答 (OMCのページ)
https://onlinemathcontest.com/contests/omc138/editorial/3171
(厳密には，公式解答のように付近での増減を調べる必要がある．)

6.

　任意の正の実数の組 (x,y) について，x+y か 4/x + 4/y のうち，少なくとも一方は 4 以上であることを示せ．

ヒント

ヒント
場合分けしてもよいが，2数の和をとると...？

解答

解答
　相加相乗平均の不等式より，
(x + y) + (4/x + 4/y) = x + 4/x + y + 4/y >= 2√4 + 2√4 = 8.
であるから，x + y か 4/x + 4/y のどちらかは4以上となる．

[補足 : 等号成立条件を確認する必要はない．]

7.

　正の実数の場合のCauchy-Schwarzの不等式を，相加相乗平均の不等式を用いて証明せよ．つまり，任意の2n個の正の実数 a_1,a_2,...,a_n,b_1,b_2,...,b_n について，次の式を示せ．

(a_1² + a_2² + ... + a_n²)(b_1² + b_2² + ... + b_n²) >= (a_1b_1 + a_2b_2 + ... + a_nb_n)²

ヒント1

ヒント1
展開してみよう．

ヒント2

ヒント2
2変数の相加相乗平均の不等式を使う．

解答

解答
展開すると，
(左辺) = 全ての 1 <= i,j <= n なる (i,j) について a_i²b_j² を足したもの
(右辺) = 全ての 1 <= i,j <= n なる (i,j) について a_i b_i a_j b_j を足したもの
となる．
i = j のときは，a_i²b_j² = a_i b_i a_j b_j である．
i≠j のときを考える．(i,j) と (j,i) をひとまとめに考えると，相加相乗平均の不等式より，
a_i²b_j² + a_j²b_i² >= 2a_ib_ja_ja_i = a_ib_ia_jb_j + a_jb_ja_ib_i が成り立つ．
よって，全体で考えれば (左辺) >= (右辺) である．

(ご存知の通り，Cauchy-Schwarzの不等式は全ての実数について成り立つ．これはここで示した正の実数ver. において，a_i → |a_i| と置き換えることにより示すことができる．各自試してみよ．)

余談

余談
　Lagrangeの恒等式 という恒等式があり，この等式を認めればCauchy-Schwarzの不等式は明らかです．Lagrangeの恒等式の証明にも (i,j) (j,i) をペアにする というアイデアが使われており，(というか上の解答とやってることほぼ同じなんですが，) 念頭に置くと証明も読みやすいと思います．
　ところで，Cauchy-Schwarzの不等式はベクトルについての不等式とも見なすことができますが，Lagrangeの恒等式もベクトルについての等式として理解できるそうです．筆者はよく分かりません．

8. (OMC132 - E)

　実数 x,y が 3x² + 2xy + 2y² = 100 を満たすとき，(2x² + xy - y²)² のとりうる最大値を求めて下さい．

ヒント1

ヒント1
2x² + xy - y² の絶対値のみに注目すればよい．

ヒント2

ヒント2
2x² + xy - y² は因数分解できる．

ヒント3

ヒント3
3x² + 2xy + 2y² を x+y と 2x-y で表してみよう．

解答

解答 (OMCのページ)
https://onlinemathcontest.com/contests/omc132/editorial/4656

(等号を成立させる x,y があることを確かめてみよ．)