幾何構図集 - OMC攻略wiki(非公式)

別ページのもの

• 垂心周りの構図　リンク: https://w.atwiki.jp/omcwiki/pages/14.html
• symmedian・調和四角形周りの構図
• 調和点列周りの構図
• 反転周りの構図

始めに

有名構図をたくさん集めます. 証明したことがない構図は是非証明してみることをオススメします.
知ってるものがあればどんどん追加してください(複雑なものはできれば画像:geogebra付きで)

0．凡例

頻出度：☆☆☆☆☆（5段階です）

以下特に断りがない限り, 三角形ABCの辺BC, CA, ABの長さをそれぞれa, b, cで, 面積をSで, 外接円の半径をRで, 内接円の半径をrで表します.

三角関数(構図じゃないから別ページにまとめたいですね～～)

1-1.ヘロンの公式

頻出度：☆☆☆

s=(a+b+c)/2とおけば, S=√s(s-a)(s-b)(s-c)

例えばa=3, b=4, c=5とおけば s=6 なので, S=√(6･3･2･1)=6 で確かに正しい.

証明

S = 1/2*bcsinA = 1/2*bc√(1-cosA^2)

ここで cosA に余弦定理をぶち込んでうまいこと変形すれば, 芳樹君が得られる.

1-2.ヘロンの公式 ~応用系~

頻出度：☆☆☆

S=1/4*√(2(a^2b^2+b^2c^2+c^2a^2)-(a^4+b^4+c^4))

例えばa=3, b=√5, c=√2とおけば a^2=9, b^2=5, c^2=2 で, S = 1/4*√(2*73-110) = 3/2 となり確かに正しい. この計算を基本形ですると面倒な計算になる.

証明

基本形の証明の途中式から導出できる.

相似系

1．回転相似

頻出度：☆☆☆

三角形ABCと三角形ADEが向きも込めて相似ならば，三角形ABDと三角形ACEも相似となる．また，(四角形BCEDが存在するとき)点Aは四角形BCEDのミケル点である．(詳しくは後述)

証明

証明
∠ABC=∠ADEより∠ABD=∠ACE，AB:AC=AD:AEよりAB:AD=AC:AEが成り立つことから.

この性質を用いた問題

• OMC093(F) 400

2.　四角形のミケル点

頻出度：☆☆☆

四角形ABCDにおいて，点E,Fをそれぞれ直線ABとCDの交点，直線BCとADの交点とする．このとき，三角形EAD,EBC,FAB,FCDの外接円は1点Pで交わり，この点を四角形ABCDのミケル点と呼ぶ．また，三角形PABと三角形PDC，三角形PBCと三角形PADはそれぞれ相似となる．

証明

証明
書きます

四角形のミケル点を用いた問題

• OMC172(C) 300
• OMC198(D) 400
• OMC100(D) 600
• OMC064(E) 700

三角形の五心系

1.　外心・垂心・内心・傍心の角度

頻出度：☆☆☆☆☆

鋭角三角形ABCにおいてその外心, 垂心, 内心, ∠A内の傍心をそれぞれO, H, I, I_Aとする.
このとき,
①∠BOC=2∠A
②∠BHC=180°-∠A
③∠BIC=90°+∠A/2
④∠BI_AC=90°-∠A/2
が成り立つ.

証明

証明
①中心角の定理より明らか.
②直線BHと直線ACの交点をD, 直線CHと直線ABの交点をEとすると四角形AEHDは円に内接する.
よって,∠BHC=∠EHD=180°-∠A
③∠BIC=180°-(∠IBC+∠ICB)=180°-(∠B+∠C)/2=180°-(180°-∠A)/2=90°+∠A/2 より.
④∠BI_AC=180°-∠I_ABC-∠I_ACB=180°-(360°-∠B-∠C)/2=180°-(180°+∠A)/2=90°-∠A/2

∠BGCは∠Aだけで定まらない. 図を書いて確かめてみよう.

2．オイラー線

頻出度：☆☆☆☆

三角形ABCにおいて，その外心O,重心G,垂心Hは同一直線上にあり，この直線をオイラー線と呼ぶ．また，重心Gは線分OHを1：2の比率に内分する．　
なお，後述する九点円の中心もオイラー線上にあるが，特にこれは線分OHの中点である．

証明

ググってください.

　外心,重心,垂心などがあるときは，オイラー線を考えると上手くいくことがある．

オイラー線を用いた問題

• OMC103(E) 300
• OMC140(F) 400
• OMC074(D) 600
• OMC024(F) 800

3．内心と傍心の相互関係

頻出度：☆☆☆☆

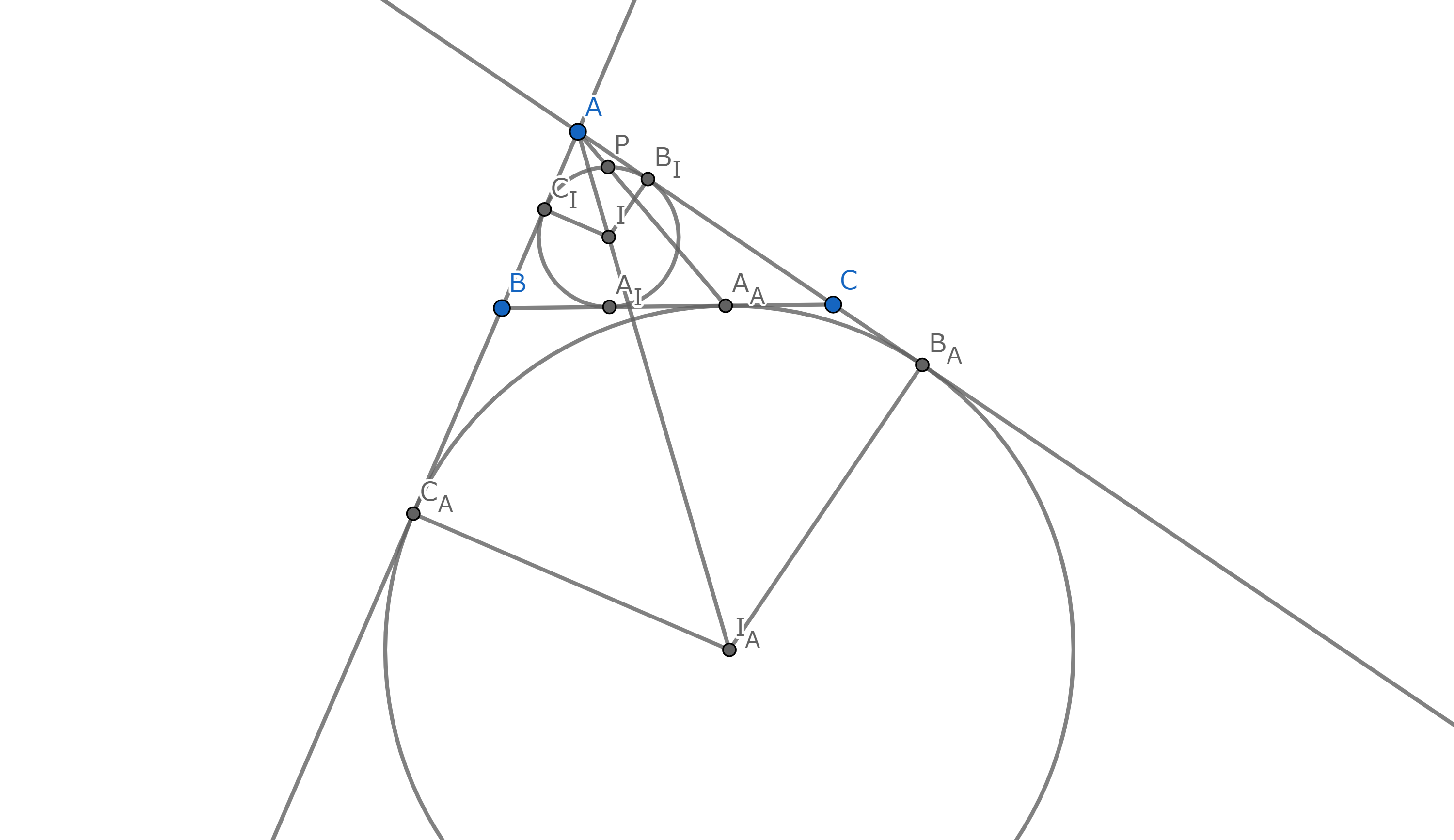
三角形ABCの内心をIとし，内接円と辺BC,CA,ABとの接点をそれぞれA_I ,B_I ,C_I とする．三角形ABCの∠A内の傍心をI_Aとし，その傍接円と直線BC,CA,ABとの接点をそれぞれA_A ,B_A ,C_A とする．また直線A_II と内接円の交点をPとする．
このとき3点A,P,A_Aは共線であり，加えてBA_I=CA_Aが成り立つ．

証明

内接円と傍接円の共通外接線の交点がAであることから，Aは2円の相似拡大変換の中心となる．この変換においてPとA_Aが対応するため3点A,P,A_Aは共線であり，BA_I=(AB+BC-CA)/2=CA_Aが成り立つ．

この性質を用いた問題

• OMC191(F) 400

4．内心と外接円の相互関係

頻出度：☆☆

三角形ABCの外接円の弧BC,CA,ABの中点をそれぞれA_C ,B_C ,C_C とする．また，ABとC_CA_Cの交点をP，CAとA_CB_Cの交点をQとする．
このときPQ//BCで，PQは三角形ABCの内心Iを通る．またBCとC_CA_Cの交点をKとすれば四角形IPBKはひし形である．

証明1

AA_C,BB_Cはそれぞれ∠A,∠Bを二等分する.
（構図5）より，IはAA_C,BB_Cの交点.弧B_CC_Cと弧BA_Cの長さの和は円周の半分なので，∠B_CA_CC_C+∠BB_CA_C=90°．すなわちBB_C⊥C_CA_Cである．
また，BB_Cは∠CBAの二等分線なので，点PとKは直線BB_Cに関して対称である.
A_CC_Cは∠AA_Cの二等分線なので，点BとIは直線A_CC_Cに関し対称である．よって四角形BKIPはひし形である．
Cにおいても同様のことがいえ，ここでBC//PIおよびBC//IQが成立することに留意すればP,I,Qの共線およびBC//PQが従う．

証明2

角度計算よりBK=BPである．また，構図5よりA_CI=A_CBおよびC_CI=C_CBが成り立つためBとIは直線A_CC_Cに関し対称となり，特に四角形BKIPはひし形である．以下証明1と同様．

この性質を用いた問題

• OMC241(D) 500

5．外接円と角の二等分線(トリリウムの定理)

頻出度：☆☆☆☆☆

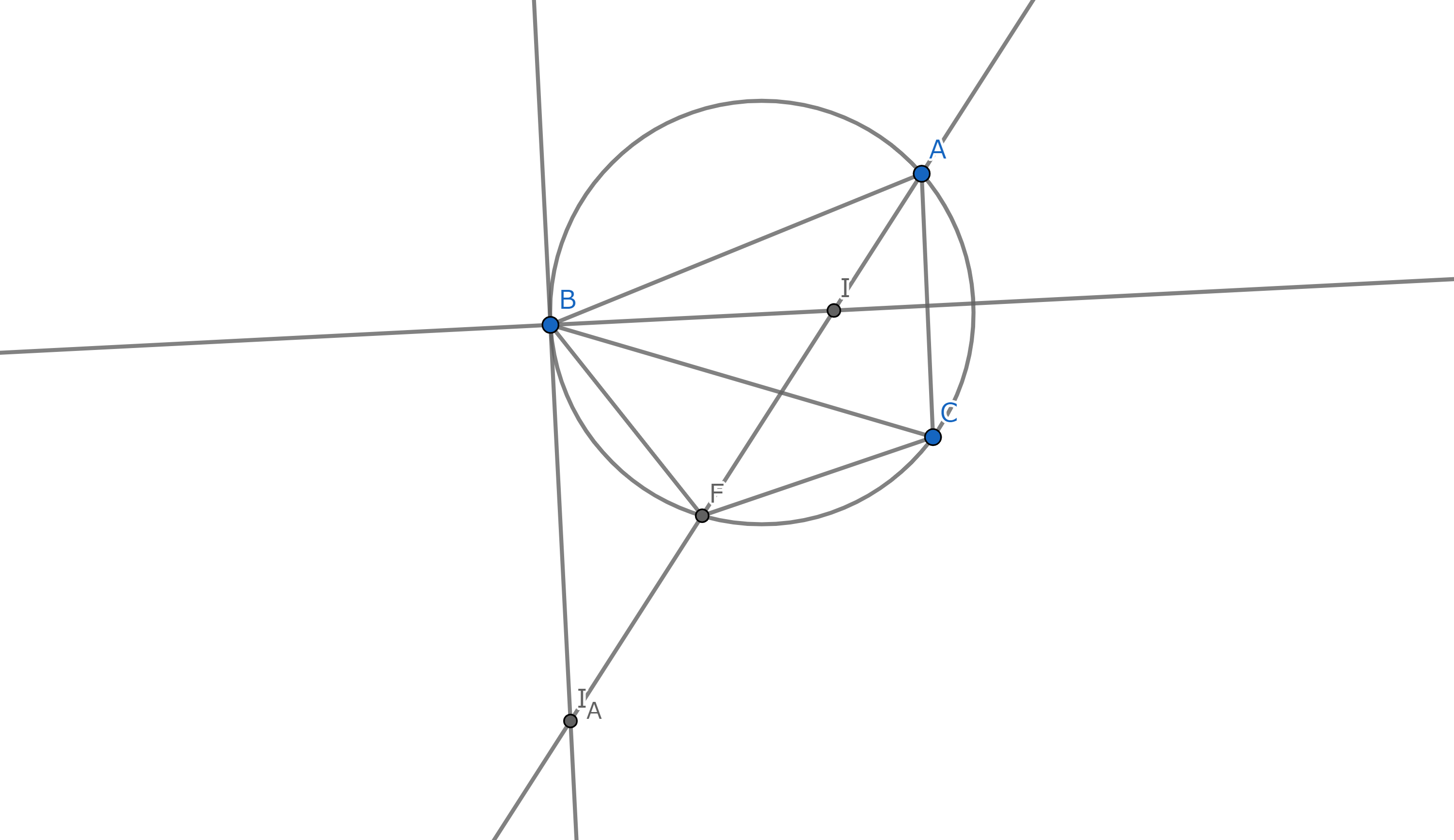
三角形ABCの内心，∠A内の傍心をそれぞれI，I_Aとし，三角形ABCの外接円と直線AIの交点（=Aを含まない弧BCの中点）をPとする．
このとき，PB=PC=PI=PI_Aが成り立つ．

(図でPはF)

証明

証明
step1.PB=PCを示す
∠PBC=∠PAC=∠PAB=∠PCB よりPB=PC
step2.PB=PIを示す
∠PBI=∠PBC+∠CBI=∠PAB+∠ABI=∠PIB よりPB=PI

この性質を用いた問題

• OMC105(F) 400
• OMC129(F) 400
• OMC132(F) 400

6-1．九点円

頻出度：☆☆☆

三角形ABCにおいてその垂心をH，辺BC,辺CA,辺ABの中点をそれぞれM_A,M_B,M_C，点A,点B,点Cから対辺に下ろした垂線の足をそれぞれD,E,F，線分AH,線分BH，線分CHの中点をそれぞれN_A,N_B,N_Cとする．
このとき，9点M_A,M_B, M_C,D,E,F,N_A,N_B,N_C は同一円周上にある.
また，上で述べた通り，この円の中心は外心と垂心の中点になる．

証明

書きます

6-2．九点円と内接円

頻出度：☆

正三角形でない三角形について，その九点円と内接円は接する．この点をフォイエルバッハ点と呼ぶ．九点円と傍接円もまた接する．（フォイエルバッハの定理）

証明

書きます

フォイエルバッハ点を用いた問題

• OMCG001(J) 1000

7．ベバン点

頻出度：☆

三角形ABCのナーゲル点Naとド·ロンシャン点Lの中点は，三角形ABCの傍接三角形の外心Vと一致する．この点をベバン点と呼ぶ．

この点を用いた問題

• ISL 200?-?(ネタバレ防止)

8．内心，外心およびベバン点の関係

頻出度：☆

三角形ABCの内心I，外心Oおよびベバン点Vについて，Iは線分OVの中点となる．

証明

I,O,Vから辺BCにおろした垂線の足をそれぞれD,M,Eとする．また，三角形ABCの角A内の傍心をJとする．角度計算から3点V,E,Jは共線となるためBD=(AB+BC-CA)/2=CEが成立し，Mが辺BCの中点となることに留意してDM=MEを得る．同様のことが辺CAにおいてもいえるためO,I,Vの共線およびOI=IVが従う．

その他（内接円関連とか）

1．OMC112(B)のやつ

頻出度：☆☆

△ABCの内接円と辺BC,CA,ABとの接点をそれぞれD,E,Fとし，点Dから直線EFに下ろした垂線の足をHとすればDHは∠BHCを二等分する．

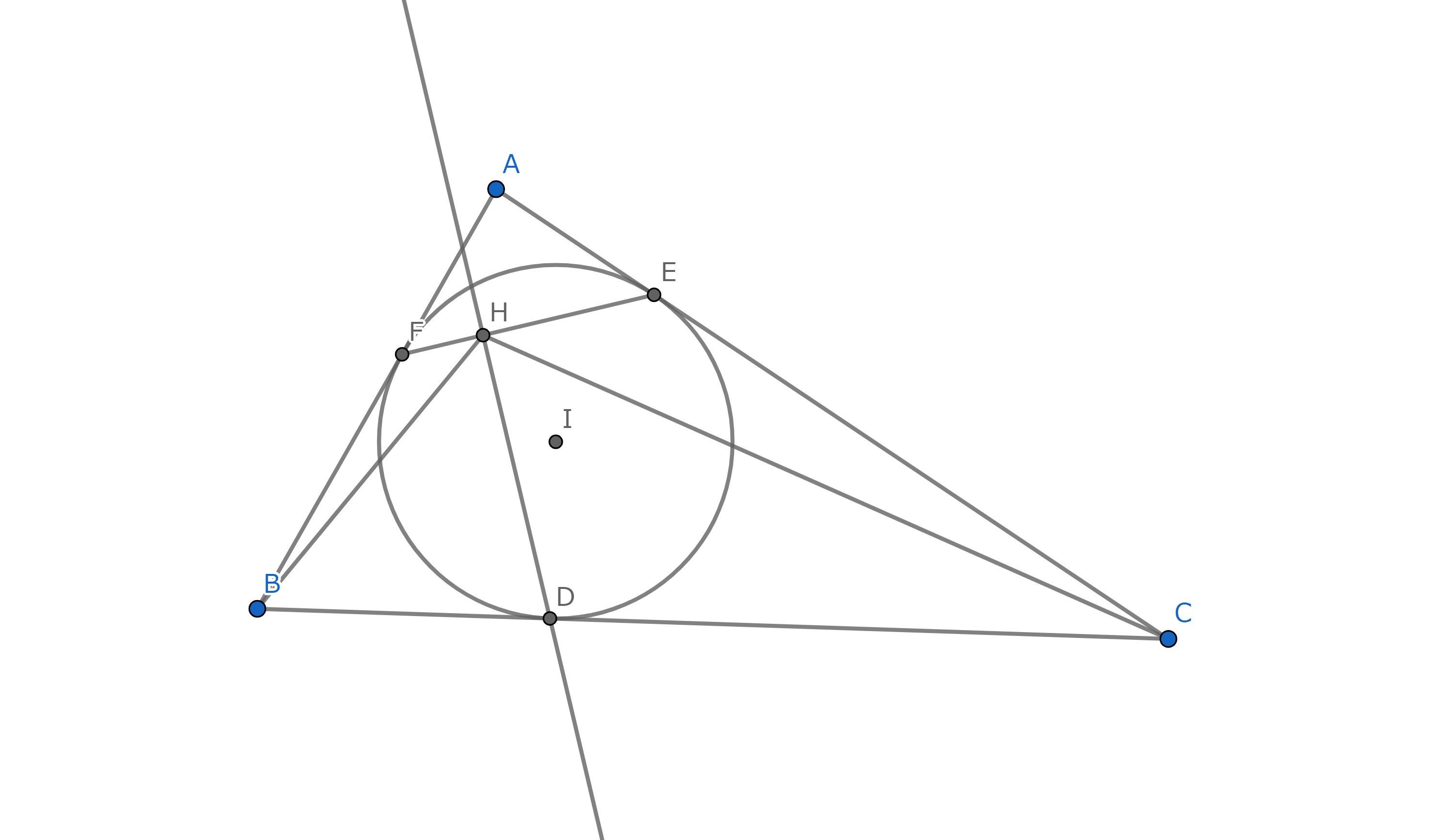
証明

直線BC,EFの交点をKとすればAD,BE,CFは一点で交わるため4点K,B,D,Cは調和点列をなす．
したがって，∠DHK=90°に留意すればDHは∠BHCを二等分する．（HはB,CにおけるDでのアポロニウスの円上となるため）

補足

より一般に，辺BC,CA,AB上にそれぞれD,E,Fを，直線AD,BE,CFが一点で交わるよう取ったとき同様の主張が成り立つ．

この性質を用いた問題

• OMC112(B) 500

2．British Flag Theorem　(イギリスの旗定理)

頻出度：☆☆☆

長方形ABCDの内部に点Pをとる．このとき，AP²+CP²=BP²+DP²が成り立つ.

証明

PからAB,BC,CD,DAに下ろした垂線の足をそれぞれE,F,G,Hとする.
三平方の定理より,
AP²+CP²=AE²+EP²+CG²+GP²=DG²+GP²+BE²+EP²=BP²+DP²
よって, AP²+CP²=BP²+DP² が成り立つ.

この定理を用いた問題

• OMC030(B) 200
• OMC113(B) 200
• OMC058(E) 300

3．正三角形とその外接円

頻出度：☆☆☆

正三角形ABCの外接円の劣弧AB上に点Dを取ると，DC=DA+DBが成立する．

証明

トレミーの定理より，
AB*DC=BC*DA+AC*DB
ここでAB=AC=BCなのでDC=DA+DBが成立．

この定理を用いた問題

• OMC167(E) 300

4．aminoの補題(Reim's theorem)

頻出度：☆☆☆

図において2つの赤線分は平行．

証明

内接四角形の定理を二回用いて同位角相等．

amino氏の解説動画

コメント

• テスト -- 運営 (2022-08-22 15:54:09)
• aminoの補題使う問題ってなんかあるんかな -- 名無し (2022-09-03 14:30:55)
• ありそうかも -- 名無しさん (2022-09-03 21:08:41)
• 本線形式だとよく見かけますがOMCだと見たことがないですねー、もし見たことのある方がいらっしゃいましたらご教示いただきたいと申します -- 名無しよん (2022-09-05 23:08:56)
• ありがとうございます -- 上3の人 (2022-09-07 23:24:38)
• どういたしましてごん☆ -- 名無しごん (2022-09-08 23:23:18)
• OMC112(B)のやつの証明めっちゃかっこいいな -- 名無しさん (2022-09-23 19:27:22)
• どんどん構図追加して欲しい！ -- 名無しさん (2025-02-11 11:02:29)
• このサイトまだ生きてたんだ..... -- 名無し (2025-02-21 20:06:07)