量子化学まとめ

シュレーディンガー方程式の導出

最終更新：2009年07月06日 22:10

quantum_mechanic

- view

メンバー限定登録/ログイン

電子の波動性と粒子性のコーナーでは、電子が波と粒子の性質を併せ持つことを説明しました。
このコーナーでは、電子の挙動を知る上で非常に重要なシュレーディンガー方程式を導出してみたいと思います。

まず、電子が波の性質を持っているので波動方程式という波に関する方程式を導き出し、
それをすこ～し改良することでシュレーディンガー方程式を得る、という流れで行きたいと思います。

まぁ、ひとつだけ注意なのですが、テストを解く上でこの章はあまり重要ではありません。
ですので、興味のない人は華麗に読み飛ばしましょう！！

流れ

波動方程式について
　　　↓
一次元波動方程式の導出
　　　↓
一次元波動方程式を解く
　　　↓
一次元波動方程式からの類推でシュレーディンガー方程式を導く

波動方程式について

波動方程式とは、波動を記述するための方程式です！
つまり、
「変位（元の位置からどれだけ動いたか）をuとすると、このuが位置や時間によってどのようになるか」
を求めるための方程式です。

波は、弦の振動などの一次元のものからもっと次元の多いものまで存在し、
それを記述するための方程式も一次元波動方程式、二次元波動方程式・・・とあるのですが、
この節では簡単のため一次元の波動方程式のみを導出することにします！

一次元波動方程式

warning！　めちゃくちゃ長いです。でも覚えて欲しいのは最後の１式だけ…

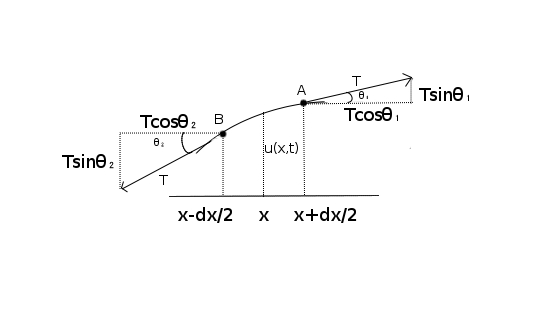
今、図のようにx軸上のx=0～l(←小文字のｴﾙです)に一本のひもがあって、これが波打ってるところを想像してください。
このひものx軸からの変位をuとおくと（横への変位もあるのですが、いまは非常に小さいと考えて省略）、
この変位uは座標xによっても、時刻tによっても違うのでu(x,t)と書きます。
で、このひもが両方から張力Tで引っ張られています。
また、このひもの単位長さ当たりの質量をρとして起きます。

さて、ここからどうやって解くかというと…運動方程式を使います。
波にどうやって使うんだよ～とおっしゃる方もいると思いますが、まぁ見ててください！

まず、運動方程式といえばF=maですよね！
これは”日本語に直すと”「物質にかかっている力は質量に加速度をかけたものと等しい」ってことですよね？
今からm，a，Fを順に求めていきます。
じゃあ、まず質量mから求めていきましょうか！

図のひものx～x+dxの部分に注目します！
この部分の質量mは{(単位長さ当たりの質量)×(長さ)｝より

$m=\rho dx$

以上でmがわかりました。次はaです。
加速度aは変位u(x,t)の2階微分なので

$a=\frac{\partial^2 u}{\partial t^2}$

以上でaがわかりました。最後Fに行ってみましょう！
まぁ、皆さん知ってのとおりFはひものx～x+dxの部分にかかっている力なので、ひもに働いている張力に注目しましょう！

で、ここで注意して欲しいのは張力はひもの両端に同じ力だけかかっているということです。
それと張力がかかる方向は、張力がかかっている部分のひもの傾きの方向であるということです。
図のようなものを想像してもらえるとわかりやすいと思います。

このように力がかかっているので、ひもの注目している部分もその合力の向きに動くのですが、
横方向への変位は非常に小さいと考えて華麗にスルー！

で、縦方向にかかる力を考えましょう。
まずは右はじ(x+dxのとこ)に注目。ここにかかる力はTsinθですね。
ここでθが非常に小さいときは次の式が成り立つというのは有名な話で

$\sin \theta \approx \tan \theta$

ここでtanθは"傾き"のことだから

$\tan \theta = \frac{\partial u}{\partial x}|_{x=x+dx}$

(偏微分の右についている|x=x+dxはx+dxのときという意味。
つまり右辺は"座標がx+dxのところの傾き"という意味！)

ですから、右はじにかかっている力の縦方向の成分は

$T\frac{\partial u}{\partial x}|_{x=x+dx}$

です。

同じようにして、左はじにかかる力の縦方向の成分を求めると

$T\frac{\partial u}{\partial x}|_{x=x}$

です。

ですから、今注目しているx～x+dxの部分にかかる縦方向の合力Fは

$F=T(\frac{\partial u}{\partial x}|_{x=x+dx}-\frac{\partial u}{\partial x}|_{x=x})$

です。

なんか複雑で見にくいですね・・・見た目よくしましょう！
そのためにはx+dxの部分をテイラー展開してやります。すると・・・

$\frac{\partial u}{\partial x}|_{x=x+dx}=\frac{\partial u}{\partial x}|_{x=x}+\frac{\partial^2 u}{\partial x^2}|_{x=x} \times dx + \cdot\cdot\cdot$

上の式の…の部分は本当はずっと続くのですが、小さいのでシカトします。こいつをさっきの見にくい式に代入してやると

$F=T(\frac{\partial u}{\partial x}|_{x=x}+\frac{\partial^2 u}{\partial x^2}|_{x=x} \times dx-\frac{\partial u}{\partial x}|_{x=x})$

$=Tdx\frac{\partial^2 u}{\partial x^2}$

…と見やすくなります。

以上でm，a，Fが求められました。こいつらを運動方程式に代入してやると…

$Tdx\frac{\partial^2 u}{\partial x^2}=\rho dx \times \frac{\partial^2 u}{\partial t^2}$

両辺をTdxで割って…

$\frac{\partial^2 u}{\partial x^2}=\frac{\rho}{T} \times \frac{\partial^2 u}{\partial t^2}$

ここで

$v=\sqrt{\frac{T}{\rho}}$ と、置くと…

$\frac{\partial^2 u}{\partial x^2}=\frac{1}{v^2} \times \frac{\partial^2 u}{\partial t^2}$

となり、めでたく一次元波動方程式が導かれました！！
また、お気づきの方もいるかもしれませんがvは速度を意味します。()

一次元波動方程式を解く！！

さて、前節で一次元波動方程式を導いたことですし、解きますか。
といってもこいつを解くには、こちらから２つほど条件を入れてやらなければならんのです。

まず一つ目の条件は境界条件と呼ばれるもので、

$u(l,t)=0$

$u(0,t)=0$

要は、ひもの両はじでは常に変位はゼロであるってこと。

二つ目は

$u(x,t)=f(x)g(t)$

と書けるという条件。つまり変位uはxだけの式とtだけの式の掛算でかけるということです。このような手法は量子化学では結構よくみる方法です。

では、早速解きましょう。
まずは、先ほど求めた波動方程式にu(x,t)=f(x)g(t)を代入してみます。すると…

$g(t)\frac{d^2 f(x)}{dx^2} = \frac{f(x)}{v^2} \frac{d^2 g(t)}{dt^2}$

この式の両辺をf(x)g(t)で割ってやると…

$\frac{1}{f(x)}\frac{d^2 f(x)}{dx^2} = \frac{1}{v^2} \frac{1}{g(t)} \frac{d^2 g(t)}{dt^2}$

この式をよく見ると、左はxだけ、右はtだけの式になってますね！
ここで少し考えてほしいのですが、x，tはそれぞれ座標、時刻なのでまったく関係なく変化しますよね？(独立)
上の式で、たとえばxだけ、もしくはtだけ変えてもイコールが成立する。
そのためには、両辺が定数になってなければなりません。
この定数をkと置くと…

$\frac{1}{f(x)}\frac{d^2 f(x)}{dx^2} = k$
$\frac{1}{v^2} \frac{1}{g(t)} \frac{d^2 g(t)}{dt^2} = k$

となります。

$\frac{d^2 f(x)}{dx^2} = kf(x)$
$\frac{d^2 g(t)}{dt^2} = kv^2g(t)$

ここでkは、実は負以外あり得ません。なぜか知りたい人以外は読み飛ばしましょう！

kが負である理由

k=0の場合
$\frac{d^2 f(x)}{dx^2} = kf(x)$ より
$\frac{d^2 f(x)}{dx^2} = 0$

これを満たすのは
$f(x) = ax+b$ のときです。

ここで境界条件

$u(l,t)=f(l)g(t)=0$

$u(0,t)=f(0)g(t)=0$ より

$f(0)=0$ , $f(l)=0$

これから

$a=b=0$ すなわち $f(x)=0$

これは、変位が常に0であるということ、つまりひもは振動しないと言っているので意味を持たない。よってk=0はあり得ない。

k=正の場合

$k=\beta ^2$ と置くと、(ただしβは0ではありません)

$\frac{d^2 f(x)}{dx^2} = kf(x)$ より
$\frac{d^2 f(x)}{dx^2} = \beta ^2 f(x)$

この方程式の一般解は

$f(x)=c_1 e^{\beta x} +c_2 e^{-\beta x}$

$f(0)=0$ ， $f(l)=0$ より

$c_1+c_2=0$

$c_1 e^{\beta l} +c_2 e^{-\beta l}=0$

この2式から

$c_1(e^{\beta l}-e^{-\beta l})=0$

$e^{\beta l} + e^{-\beta l} \ne 0$ ですから

$c_1=0$

$c_1+c_2=0$ より

$c_2=0$

よって、
$f(x)=0$

これは、ひもが振動しないということをあらわしているので、物理的な意味がありません。
よってkは正ではない。

k=負の場合

$k=-\alpha ^2$ と置くと、(ただしαは0ではありません)

$\frac{d^2 f(x)}{dx^2} = kf(x)$ より
$\frac{d^2 f(x)}{dx^2} = -\alpha ^2 f(x)$

この方程式の一般解は
$f(x)=A\cos{\alpha x} + B\sin{\alpha x}$
です。

$f(0)=0$ より
$f(0)=A=0$

よって
$f(x)=B\sin{\alpha x}$

$f(l)=0$ より

$f(l)=B\sin{\alpha l}=0$

B=0だとf(x)=0となりひもが振動しないので
$\sin{\alpha l}=0$

よって
$\alpha l=n \pi$ 　ただしnは整数

簡単のためにB=1と置くと、
$f_n (x)=\sin{\frac{n\pi x}{l}}$ ただしnは整数
と、なる。

ここでnに注目してください

ｎ=0の時
$f_0 (x)=0$
となってひもは振動せず、物理的に意味がありません。

それと、nが負の時

これは、f(x)の正負が入れ替わるだけなので同じとみなします。

(例)
$n=-1$ のとき
$f_{-1} (x)=\sin{-\frac{\pi x}{l}}=-\sin{\frac{\pi x}{l}}=-f_1 (x)$

以上のことを踏まえて
$f_n (x)=\sin{\frac{n\pi x}{l}}$ $(n=1,2,3\cdot\cdot\cdot)$

これでやっとf(x)に関して解けました！！

g(t)に関しても同様に解けます。(ただしg(t)には境界条件はないので少しだけ違います。)

答えだけのせておくと…
$g(t)=\cos{(\omega_n t+ \phi_n)}$ ただし、 $\omega_n = \frac{n\pi v}{l}$

よって、波動方程式の解は
$u(x,t)=f_n (x)g_n (t)=\sin{\frac{n\pi x}{l}}\cos{(\omega_n t+ \phi_n)}$

(ただしこれの定数倍も解なのですが簡単のために省略します。)

いやぁ、やっと解けました！長かったですね～(笑)。次はいよいよシュレーディンガー方程式を導きますよ！

一次元波動方程式からの類推でシュレーディンガー方程式を導く

前節で導いたことをまとめると…

一次元波動方程式

$\frac{\partial^2 u}{\partial x^2}=\frac{1}{v^2} \frac{\partial^2 u}{\partial t^2}$

一次元波動方程式の解

$u(x,t)=f_n (x)g_n (t)=\sin{\frac{n\pi x}{l}}\cos{(\omega_n t+ \phi_n)}$

この解のf(x)をψ(x)に変えて、波動方程式に代入してやると、
(ψは波動関数または固有関数と呼ばれます)

$\frac{\d^2 \psi (x)}{d x^2} \cos{\omega t} + \frac{\omega^2}{v^2} \psi (x)\cos{\omega t} = 0$

ただし、簡単のため
$\omega_n=\omega$ ， $\phi_n=0$
とした。

両辺をcos(ωt)で割って…

$\frac{d^2 \psi (x)}{d x^2} + \frac{\omega^2}{v^2} \psi (x) = 0$

ここで、

$\omega=2\pi \nu$ より (ただしνは振動数です。)

$\frac{\omega ^2}{v^2}=\frac{4\pi ^2 \nu ^2}{v^2}$

さらに、

$v=\lambda \nu$ より　　　(ただしλは波長です。)

$\frac{\omega ^2}{v^2}=\frac{4\pi ^2}{\lambda ^2}$

ここで、ド・ブロイの式
$P=\frac{h}{\lambda}$
を使うと…

$\frac{\omega ^2}{v^2}=\frac{4\pi ^2}{\lambda ^2}=\frac{p^2}{\hbar ^2}$

ただし

$\hbar=\frac{h}{2\pi}$

よって、

$\frac{d^2 \psi (x)}{d x^2} + \frac{p^2}{\hbar ^2} \psi (x) = 0$

ここで、電子の持つ全エネルギーをE、運動エネルギーをT、ポテンシャルエネルギーをU(x)とすると、

$T=\frac{1}{2}mv^2=\frac{(mv)^2}{2m}=\frac{p^2}{2m}$ より

$E=T+U(x)=\frac{p^2}{2m}$

よって

$p^2=2m(E-U(x))$

これを先ほどの式に代入して

$\frac{d^2 \psi (x)}{d x^2} + \frac{2m(E-U(x))}{\hbar ^2} \psi (x) = 0$

すこし整理してやって

$-\frac{\hbar ^2}{2m} \frac{d^2 \psi (x)}{dx^2} + U(x)\psi (x) = E\psi (x)$

左辺をψ(x)でくくってやると

$[-\frac{\hbar ^2}{2m} \frac{d^2}{dx^2}+U(x)]\psi(x)=E\psi (x)$

これが時間に依存しないシュレーディンガー方程式と呼ばれるものです！！！
("時間に依存しない"とはたとえば原子の電子状態など時間に関係ない現象に関して使えるということ。)

また、

$\hat{H}=-\frac{\hbar ^2}{2m} \frac{d^2}{dx^2}+U(x)}$

として

$\hat{H} \psi (x)= E\psi (x)$

と、簡単に書くこともあります。Hはハミルトニアンといいます。

かなり長くなってしまいましたが、以上でこの章は終わりです。

覚えて欲しいのは最後の2式です。

「シュレーディンガー方程式の導出」をウィキ内検索

添付ファイル

img001.jpg

人気記事ランキング

最近更新されたページ

新規Wikiランキング

最近作成されたWikiのアクセスランキングです。見るだけでなく加筆してみよう！

人気Wikiランキング

atwikiでよく見られているWikiのランキングです。新しい情報を発見してみよう！

全体ページランキング

最近アクセスの多かったページランキングです。話題のページを見に行こう！

シュレーディンガー方程式の導出

流れ

波動方程式について

一次元波動方程式

一次元波動方程式を解く！！

kが負である理由

一次元波動方程式からの類推でシュレーディンガー方程式を導く

一次元波動方程式

一次元波動方程式の解

メニュー

リンク

他のサービス

更新履歴