管理メニュー

量子化学まとめ

井戸型ポテンシャル

最終更新：2009年07月06日 23:05

quantum_mechanic

- view

メンバー限定登録/ログイン

さて、前章では、シュレーディンガー方程式を導いたわけですが、
この章ではシュレーディンガー方程式のもっとも簡単な例である、井戸型ポテンシャルの中の電子について考えましょう！！

流れ

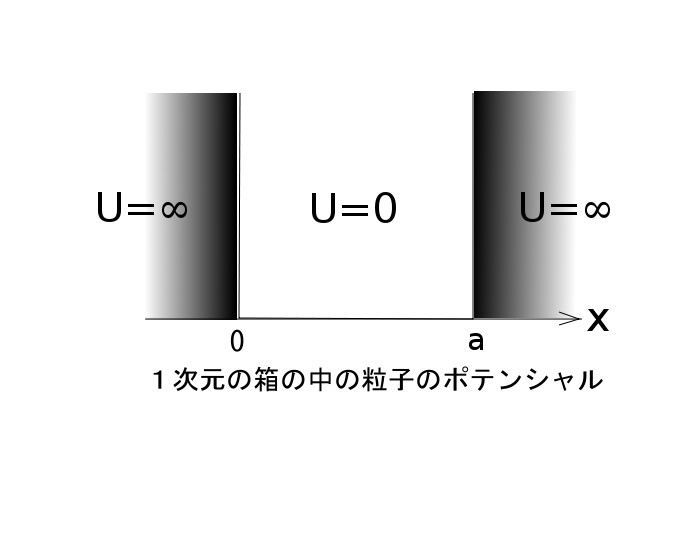
図のように空間を考えます。すなわちポテンシャルエネルギーU(x)が
$U(x)=\begin{cases}\infty\ \ \ (x<0)\\0 \ \ \ \ (0\le x \le a)\\\infty \ \ \ (a<x)\end{cases}$

図をよ～く見ると何か井戸っぽい感じがしませんか？

では、まず井戸の底、すなわちU(x)=0の部分を考えます。

ハミルトニアンHは
$\hat{H}=-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+U(x)$

今U(x)=0の時を考えているので
$\hat{H}=-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}$

です。だからシュレーディンガー方程式は

$-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\psi(x)=E\psi(x)$

変形して
$-\frac{\hbar^2}{2mE}\frac{d^2}{dx^2}\psi(x)=\psi(x)$

$-\frac{\hbar^2}{2mE}=\frac{1}{k^2}$

と、置くと
$\frac{d^2}{dx^2}\psi(x)=-k^2 \psi(x)$

この式はめっちゃくちゃ有名で、この微分方程式の解は
$\psi(x)=A\cos{kx}+B\sin{kx}$

です。(実際に解になっているかどうか各自試してみてください！)

次に境界条件を考えます。

x=0，x=aの所でポテンシャルエネルギーが無限大になるということは
$\psi(0)=\psi(a)=0$

を意味します。(※なぜこのようにするかはこの章の後の方でわかってきます)

$\psi(0)=0$ 　　を先ほどの解に代入して
$A=0$

よって
$\psi(x)=B\sin{kx}$

$\psi(a)=0$ 　　　をこれに代入して

$B\sin{ka}=0$

ここで

$B=0$

とすると、

$\psi(x)=0$

となって物理的に意味がない。
したがって

$\sin{ka}=0$

と、すると

$ka=n\pi$

すなわち

$k=\frac{n\pi}{a}$

よって、

$\psi(x)=B\sin{\frac{n\pi}{a}x}$

ところで、さっき

$-\frac{\hbar^2}{2mE}=\frac{1}{k^2}$

と、置いたので

$E=\frac{\hbar^2 k^2}{2m}$

$k=\frac{n\pi}{a}$ より

$E=\frac{\hbar^2\pi^2n^2}{2ma^2}=\frac{h^2n^2}{8ma^2}$

さてこれでとりあえず一次元シュレーディンガー方程式が解けたわけですが、
先ほどから頻繁にでてくる波動関数ψ(x)とははたして何なのでしょうか？

実はこの波動関数の２乗は電子の存在確率を表しているのです！

より正確に言うと

$|\psi(x)|^2dx(=\psi^{\ast}(x)\psi(x)dx)$

が、x~x+dxに電子が存在する確率に比例するのです！(←ここ重要)
こう考えるといろいろとうまくこじつけることができます。

じゃ、とりあえずさっきの一次元井戸型ポテンシャルについてもう一度振り返ってみましょう。
一次元井戸型ポテンシャルでは、ポテンシャルエネルギーU(x)は、

$U(x)=\begin{cases}\infty\ \ \ (x<0)\\0 \ \ \ \ (0\le x \le a)\\\infty \ \ \ (a<x)\end{cases}$

でした。

ポテンシャルエネルギーとは、電子が感じる壁のようなものです。
x=0~a以外では、U(x)=∞ですので、電子の目の前には高さが無限大の壁が立ちはだかっているようなもので、電子はその領域にはいけません。

したがって、x<0，a<xの領域では(存在確率)=ψ(x)の２乗=0となり、したがって、x<0，a<xの領域では

$\psi(x)=0$

となります。

また、x=0，x=aのところは壁と平地の境界となるわけですが、
この境界で突然電子の存在確率が大きく(不連続に)変化してしまっては不自然です。
したがって、x=0，x=aでは

$\psi(x)=0$

となります。

規格化

また、確率といえば忘れてはならない重要なことが一つあります。
それは全確率は１であるということ。
これは、古今東西変わらない事実でしょう。

先ほど、

$|\psi(x)|^2dx(=\psi^{\ast}(x)\psi(x)dx)$

が、x~x+dxに電子が存在する確率に比例するのです！と、言いました。
ですからこれを全空間で足し合わせると１になります。
これを式にすると

$\int_{-\infty}^{\infty} |\psi(x)|^2\,dx=1$

これに、井戸型ポテンシャルで導いた

$\psi(x)=B\sin{\frac{n\pi}{a}x}$

を代入してみます。

$B^2\int_{-\infty}^{\infty} \sin^2{\frac{n\pi}{a}x}\,dx=B^2\int_{0}^{a} \sin^2{\frac{n\pi}{a}x}\,dx$
(ここで波動関数が０の所は積分しても０なので考えていません。)

$=B^2\int_{0}^{a} \frac{1-\cos{\frac{2n\pi}{a}x}}{2}\,dx$

$=\frac{B^2}{2}\int_{0}^{a} 1-\cos{\frac{2n\pi}{a}x}\,dx$

$=\frac{B^2}{2}[ 1-\frac{a}{2n\pi}\sin{\frac{2n\pi}{a}x}]_0^a$

$\frac{B^2a}{2}=1$

よって

$B=\sqrt{\frac{2}{a}}$

これより、波動関数ψ(x)は

$\psi(x)=\sqrt{\frac{2}{a}}\sin{\frac{n\pi}{a}x}$

以上で一次元井戸型ポテンシャルについて波動関数が解けました。

「井戸型ポテンシャル」をウィキ内検索

添付ファイル

img003.jpg

人気記事ランキング

もっと見る

最近更新されたページ

もっと見る

新規Wikiランキング

最近作成されたWikiのアクセスランキングです。見るだけでなく加筆してみよう！

もっと見る

人気Wikiランキング

atwikiでよく見られているWikiのランキングです。新しい情報を発見してみよう！

もっと見る

全体ページランキング

最近アクセスの多かったページランキングです。話題のページを見に行こう！

もっと見る