捕手実験1
ver3.4.11
概要
Aチーム大島康平の各守備パラメータを20下げたセーブデータを、無修正のものも含めて5つ用意した。
それぞれのセーブデータを20シーズンずつ回し勝率を比較し、守備パラメータの重要度に優劣を付けることを目的とした。
しかし、測定された勝率はいずれも95%信頼区間の範囲内であり、統計的に有意な結果は得られなかった。
それぞれのセーブデータを20シーズンずつ回し勝率を比較し、守備パラメータの重要度に優劣を付けることを目的とした。
しかし、測定された勝率はいずれも95%信頼区間の範囲内であり、統計的に有意な結果は得られなかった。
先行実験
「ペナントシミュレーション part14」より引用
222名無しさん@お腹いっぱい。2019/08/15(木) 03:15:20.33ID:RO0KM1IP 監督に起用任せると総合値低くてもリードが高い捕手使いたがるから困る 打撃で何点損してると思ってんだよ 223名無しさん@お腹いっぱい。2019/08/15(木) 03:27:21.13ID:wxj3ciUd 監督「FAXでフロントから届いてくる起用マジうぜぇ…リードで何点損してると思ってんだよ」 224名無しさん@お腹いっぱい。2019/08/15(木) 03:47:21.37ID:bRqFUJ90 >>222 年間通して5点くらいか? 226名無しさん@お腹いっぱい。2019/08/15(木) 10:07:56.54ID:e+Dv//Iq リードは捕手スタメンやってれば毎年上がるからリード以外の守備能力が重要だと思う 捕手の打撃とリードなら打撃の方が価値があるけど打撃と守備能力全般なら守備能力のが欲しい 227名無しさん@お腹いっぱい。2019/08/15(木) 19:30:29.69ID:heodQAi3 リードどこまで影響あるのかよくわからん レギュラーの捕手追い出して若手使ったら失点100増えて 次の年その若手のリードが上がって失点100減った 他の野手投手はあんまり変化無かったのに 229名無しさん@お腹いっぱい。2019/08/15(木) 21:52:48.46ID:K1Lv845D 総合600の打撃守備それなりの捕手よりも 総合550の守備型捕手のほうが使われてたりするのちょっと気に食わないんだけど 捕手守備の影響度考えるとこっちのほうが勝てるんだろうな 230名無しさん@お腹いっぱい。2019/08/15(木) 22:17:03.46ID:Bo/4xxF6 >>229 俺はめんどくさいからやらないけど、セーブして何度か試してみればいい A捕手を他球団に渡して10シーズン回して(10回リセットして)勝数を数える B捕手を他球団に渡して10シーズン回して(10回リセットして)勝数を数える 235名無しさん@お腹いっぱい。2019/08/15(木) 23:56:09.81ID:K1Lv845D >>230 https://i.imgur.com/tRigYgZ.png 捕手レギュラー固定、怪我なし設定でKチーム1年目のシーズンを10回ずつスキップしてみた やっぱ守備型捕手つえーわ半端な打撃型使うメリットないなこれ

このような実験が行われた訳であるが、これだけだと守備パラメータの中のどれが特に重要なのか分からない。また、後述の信頼区間の問題も存在することから本実験を行うに至った。
信頼区間
詳しくはWikipediaでも見て欲しい。
簡潔に言うと、「X%信頼区間で、勝率がAからBの間」という事は、「あるセーブデータを1シーズン回したとき、勝率がAからBの範囲に収まる確率がX%」という意味である。
特に結果が勝ち負けの2種類しかない実験の場合は、
簡潔に言うと、「X%信頼区間で、勝率がAからBの間」という事は、「あるセーブデータを1シーズン回したとき、勝率がAからBの範囲に収まる確率がX%」という意味である。
特に結果が勝ち負けの2種類しかない実験の場合は、
A = 算術平均勝率 - 誤差幅 B = 算術平均勝率 + 誤差幅
という形で表わされる。
誤差幅をE、引き分けを除いた試合数をg、勝率をaとすると、この実験の95%信頼区間は
E = 1.96 * {a(1-a)/g}^(1/2)
である。1.96は95%の場合の定数で、例えば90%の場合は1.64になる。
さて、先程の先行実験の90%信頼区間を調べてみよう。
野上の場合は
野上の場合は
E = 1.64 * {a(1-a)/g}^(1/2) = 1.64 * {0.484*(1-0.484) / (143*10-32)}^(1/2) = 0.022
鈴木の場合は
E = 1.64 * {a(1-a)/g}^(1/2) = 1.64 * {0.493*(1-0.493) / (143*10-32)}^(1/2) = 0.022
したがって、双方共に上下に2.2%の誤差を持つことが分かる。両者の勝率差は1%にも満たないため、これだとどちらの勝率の方が上らしいのか分からない。
実験手順
本実験の手順を示す。
1.OPTIONを下のように変更した。怪我の運に結果が左右されないように「怪我なし」、スキップを高速化させるために「二軍試合なし」とした。


2.NEW GAME(新データ)でAチームを選択、支配下ドラフトは適当に投手1人指名して、それ以外は全てスルーした。
3.怪我人の確認(勿論怪我人はいない)が終わったらすぐにセーブした。
4.SQuirreL SQL Clientを用いて選手能力を編集し、Aチームの大島以外の捕手を捕手適性以外オール20にした。画像では見えないが、選球や小技も20になっている。
このセーブデータが基本のデータ、無修正の大島康平となる。
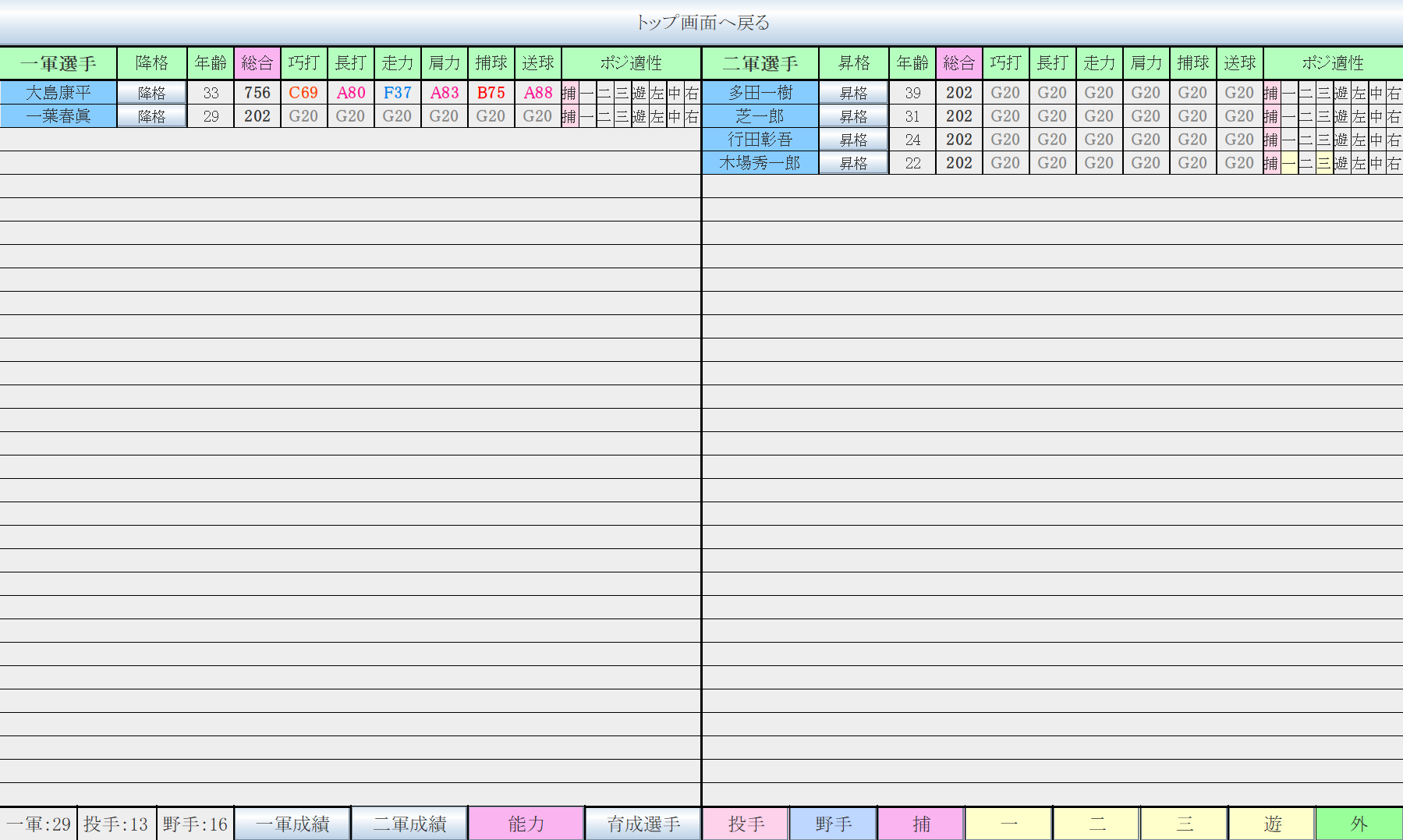
このセーブデータが基本のデータ、無修正の大島康平となる。

5.4.で作ったセーブデータをもとに、大島の肩力を20下げたセーブデータ、捕球を20下げたセーブデータ、送球を20下げたセーブデータ、リードを20下げたセーブデータを作成した。
無修正のものも合わせて5つのセーブデータを得た。
無修正のものも合わせて5つのセーブデータを得た。
| + | 無修正と修正後の大島*4 |
6.5つのセーブデータを20シーズンずつ回し、勝利数、敗北数、引き分け数、得点、失点、防御率を記録した。
実験結果
それぞれ20年回した結果は次のようになった。
無修正
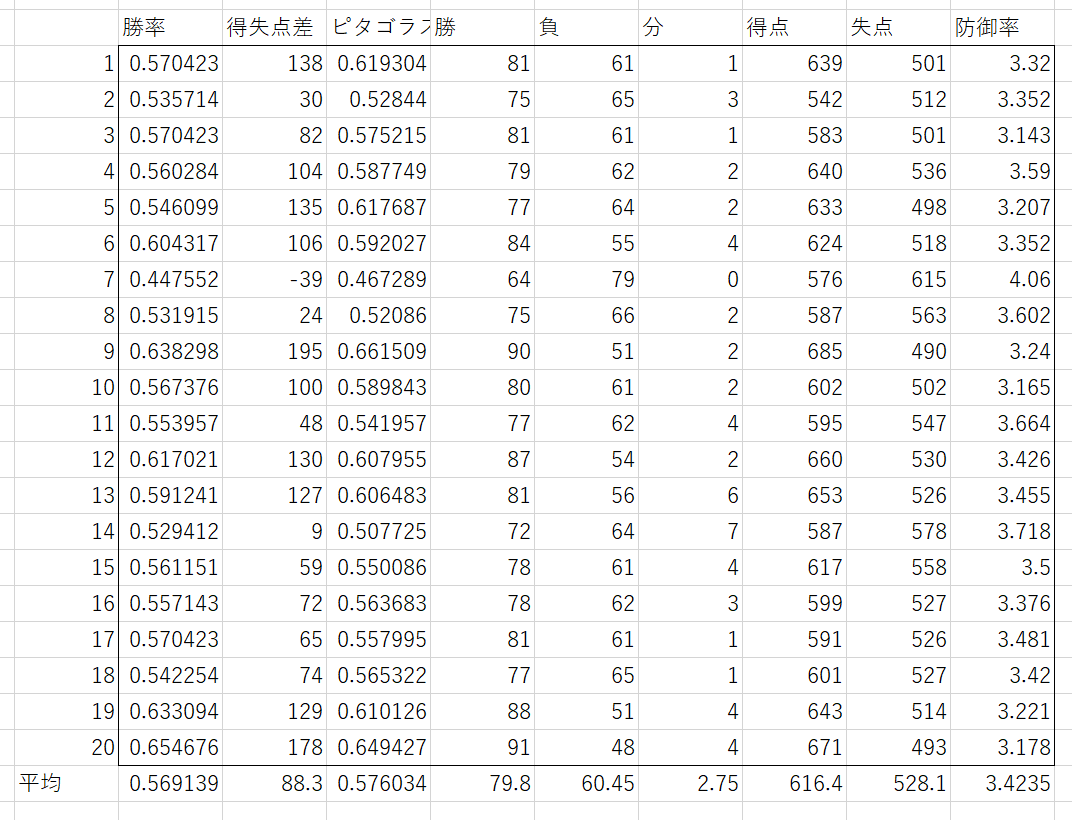
肩力-20
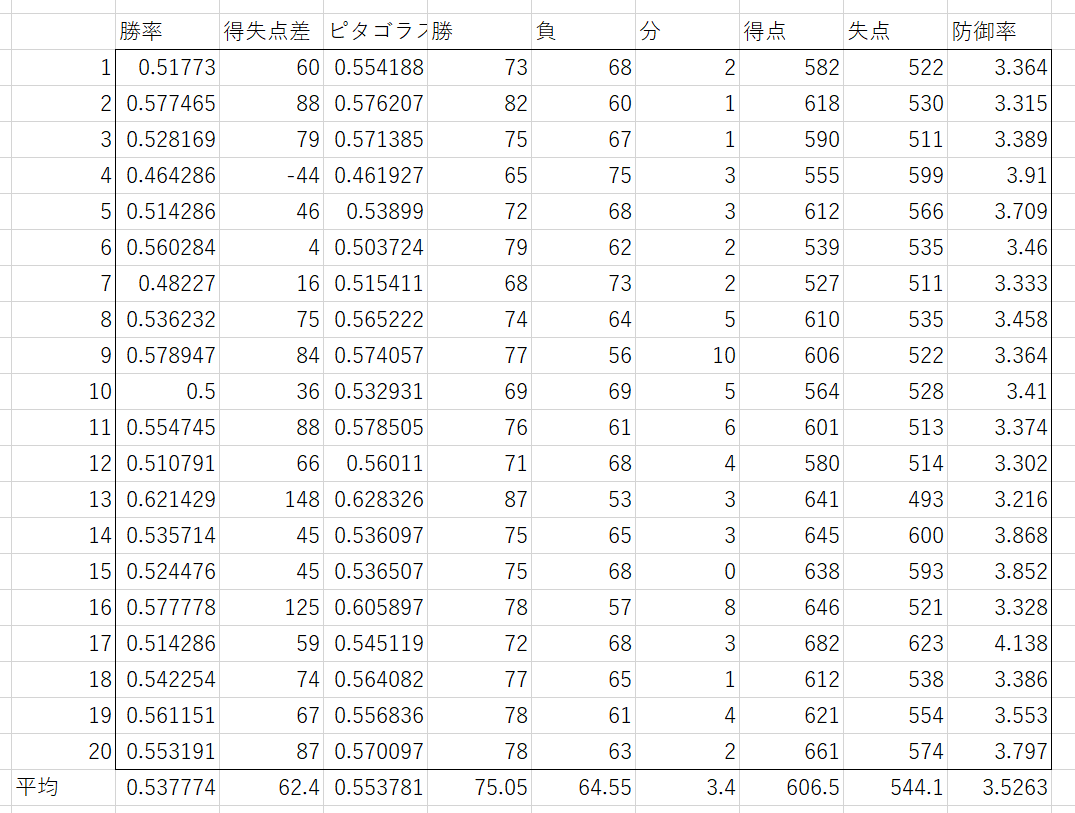
捕球-20
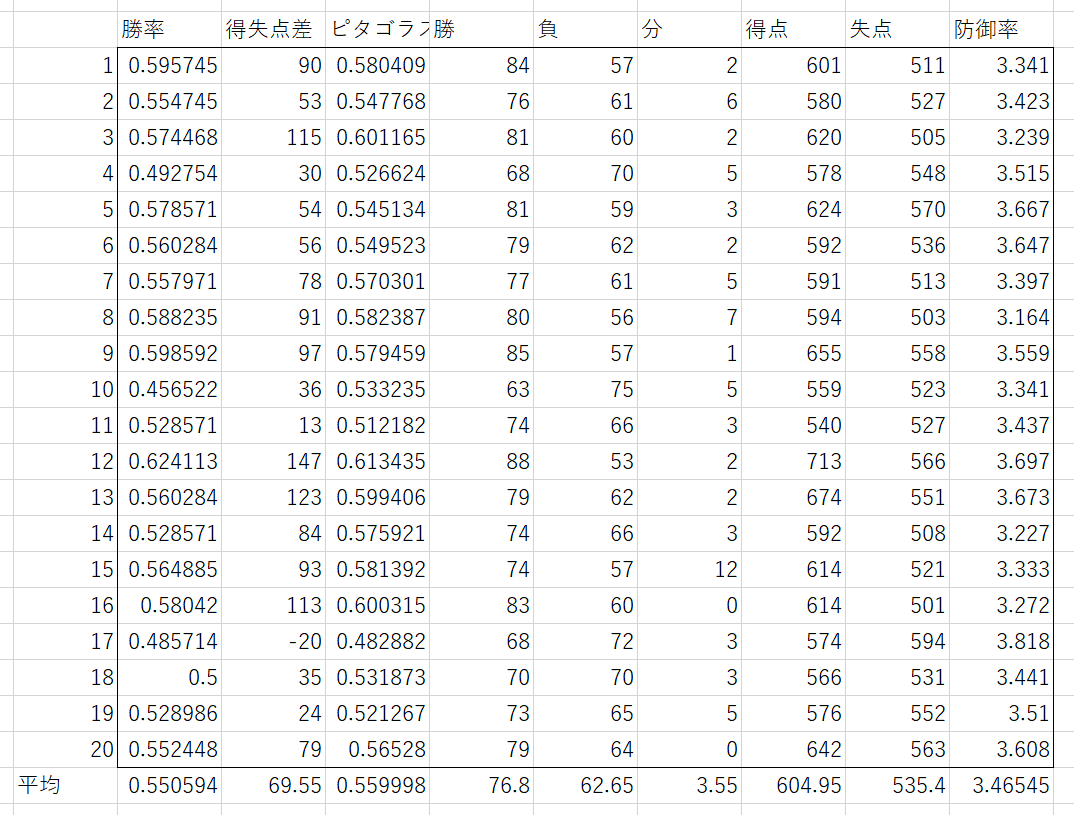
送球-20
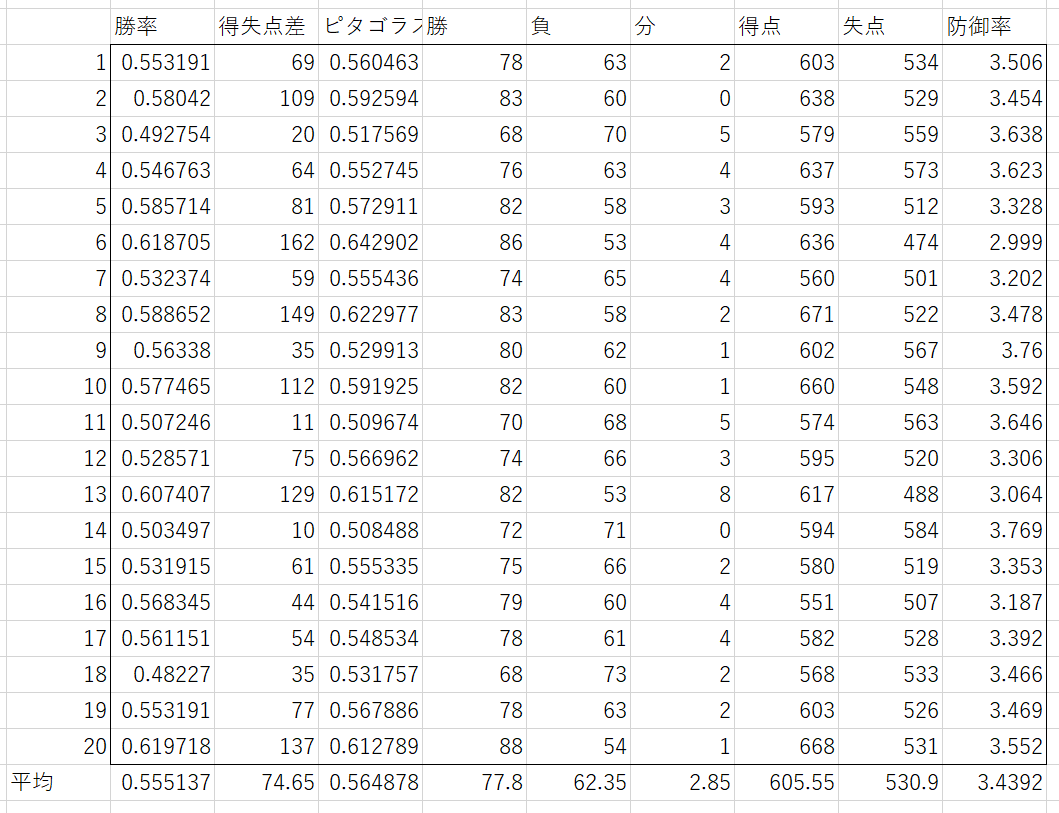
リード-20
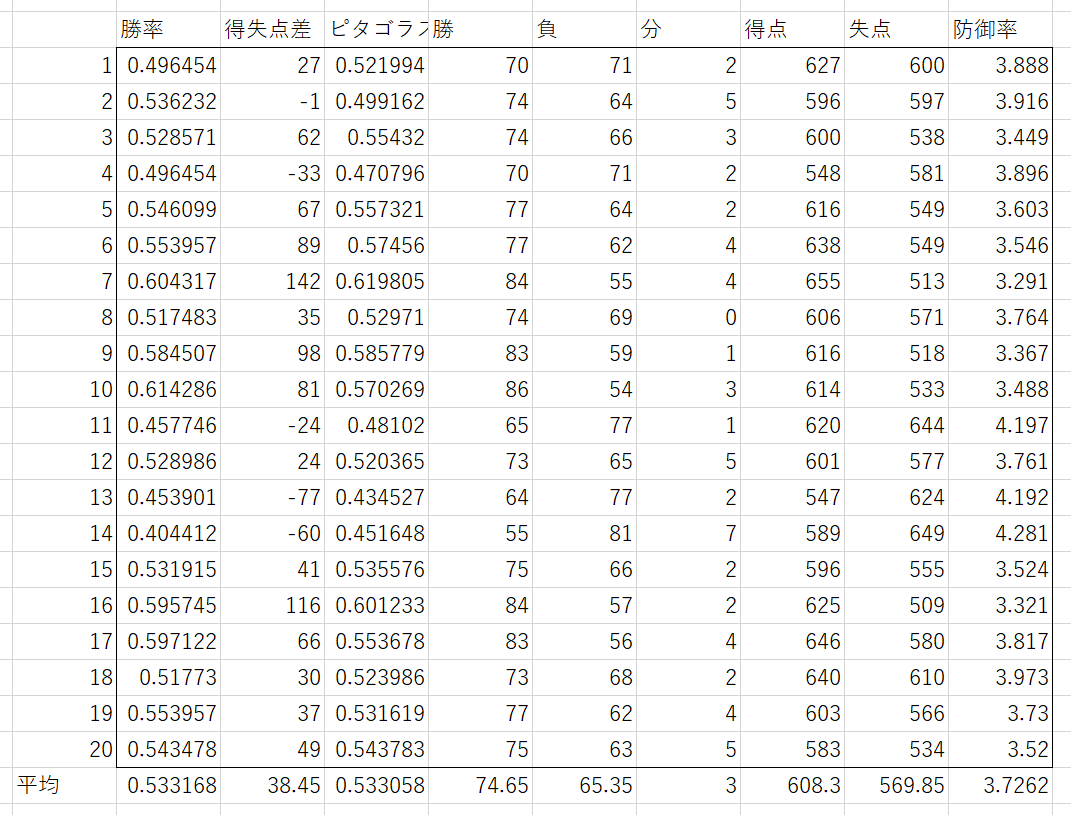
無修正

肩力-20

捕球-20

送球-20

リード-20

まとめると次のようになった。誤差±は95%信頼区間である。
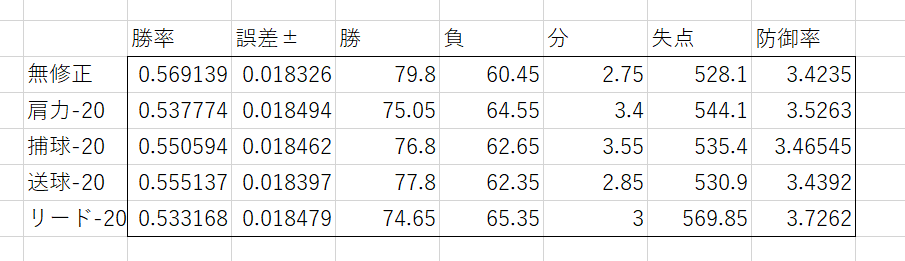

解説
最も勝率差の大きかった無修正とリード-20の場合を比較しても、その勝率差は誤差の和より小さい。
統計的に有意であるとは言い難い。
仮に信頼区間を小さく取ってこの2つ間に有意な差があるという結果にしたとしても、それは自明の結果を述べているに過ぎない。
統計的に有意であるとは言い難い。
仮に信頼区間を小さく取ってこの2つ間に有意な差があるという結果にしたとしても、それは自明の結果を述べているに過ぎない。




