TRIC-006-01 - tri-obog @ ウィキ

１次試験回答[TRIC-006-01]

2012年4月29日に行われた１次試験にて、TECRAが回答した内容を載せる。

回答一覧

午前：専門試験問題

問	回答	正解	問	回答	正解	問	回答	正解	問	回答	正解	問	回答	正解	問	回答	正解
1	3	3	31	-	3	61	-	1	91	4	4	121	-	3	151	-	2
2	4	4	32	5	4	62	-	1	92	5	5	122	-	4	152	-	4
3	1	1	33	3	1	63	-	3	93	2	2	123	-	2	153	-	3
4	2	3	34	-	1	64	-	5	94	3	3	124	-	2	154	-	3
5	1	1	35	-	5	65	-	3	95	3	3	125	-	2	155	-	1
6	1	1	36	4	5	66	-	3	96	5	5	126	-	5	156	-	4
7	4	4	37	-	2	67	-	4	97	3	3	127	-	1	157	-	2
8	3	3	38	4	4	68	-	2	98	4	4	128	-	3	158	-	3
9	2	2	39	-	4	69	-	1	99	5	5	129	-	1	159	-	4
10	2	2	40	1	1	70	-	1	100	3	1	130	-	1	160	-	5
11	5	2	41	-	1	71	-	1	101	-	5	131	-	5	161	-	3
12	2	4	42	-	3	72	-	5	102	-	2	132	-	5	162	-	5
13	5	5	43	-	2	73	-	3	103	-	5	133	-	3	163	-	3
14	1	1	44	-	3	74	-	5	104	-	3	134	-	4	164	-	3
15	5	5	45	-	5	75	-	2	105	-	1	135	-	3	165	-	5
16	5	5	46	-	4	76	-	4	106	-	3	136	-	2
17	4	2	47	1	2	77	-	1	107	-	1	137	-	4
18	5	5	48	-	1	78	-	2	108	-	5	138	-	5
19	2	2	49	-	4	79	-	3	109	-	2	139	-	3
20	5	5	50	-	4	80	-	4	110	-	4	140	-	3
21	-	4	51	-	4	81	-	5	111	-	3	141	-	1
22	-	2	52	-	5	82	-	2	112	-	4	142	-	4
23	-	3	53	-	3	83	-	4	113	-	2	143	-	1
24	-	4	54	-	1	84	-	1	114	-	4	144	-	5
25	-	2	55	-	4	85	-	2	115	-	3	145	-	2
26	5	5	56	-	5	86	-	3	116	-	1	146	-	3
27	-	4	57	-	1	87	-	1	117	-	3	147	-	4
28	3	3	58	-	1	88	-	2	118	-	4	148	-	2
29	1	2	59	-	4	89	-	1	119	-	1	149	-	5
30	2	2	60	-	2	90	-	3	120	-	2	150	-	2

結果：30/40

午後：基礎試験問題

問	回答	正解	問	回答	正解	問	回答	正解
1	4	4	11	5	5	21	3	3
2	4	4	12	2	2	22	4	4
3	2	3	13	3	3	23	3	3
4	5	5	14	4	4	24	2	4
5	1	5	15	4	1	25	4	5
6	3	1	16	2	2	26	3	3
7	4	5	17	3	2	27	5	4
8	3	5	18	4	4	28	2	2
9	2	2	19	1	1	29	1	1
10	1	1	20	4	4	30	3	3

結果：20/30

回答詳細

※あくまで自分の解き方・考え方を書いたものであり、答えを保証するものではありません。

午前：専門試験問題

問1

20^3を素因数分解すると2^6×5^3となる。
正の約数の総和を求める為には素因数の総当りを考えれば良いので、
(1+2+2^2+2^3+2^4+2^5+2^6)(1+5+5^2+2^3)
=(128-1)/(2-1)×(625-1)/(5-1)
=127×156
=19812

問2

l:√3x+y-√3=0
より、x切片1を得る。
lを反時計回りに回転させた式は
m:-x+√3y-√3=0
となる(グラフに書き起こすと分かりやすい)。
lと同様に、x切片-√3を得る。
lとmを連立して、
x=(3-√3)/4 (xについては回答に不要なので別に計算しなくとも良い)
y=(3+√3)/4
S=1/2×(1+√3)×(3+√3)/4
=(3+4√3+3)/8
=(3+2√3)/4

問3

xyz座標でA(√2, 0, 0), B(0, √2, 0), C(0, 0, √2)の3点を通る平面と原点との距離を求めれば良い。
平面と原点との距離を求める式を使うのが手っ取り早いが、式を忘れたので別の方法を用いた。
三角錐OAB-Cの体積をVとして、OABを底面と考えると
V=1/3×(1/2×√2×√2)×√2
=√2/3　－①
一方で原点と平面ABCの距離をhとし、ABCを底面と考えると
ABCの面積S=1/2×2×√3=√3
V=1/3×S×h=√3h/3　－②
①=②なので
√2/3=√3h/3
h=√6/3

問4

正直、解法が分からなかった。
分母を有理化してみたが式が複雑になっただけだった。
ロピタルの定理を使うのだろうか？
適当に選んでしまったが、良く考えたらx→0に+0から近づいても-0から近づいても
同じ値に収束しないといけないのだから、-1に収束することは計算しなくても導けたのかもしれない。

問5

e^xは常に正なので、1-x^2≧0になる範囲を求めてx=-1～1の範囲で積分を行うと、
∫[-1, 1] (1-x^2)e^x dx
=[(1-x^2)e^x][-1, 1] - ∫[-1, 1] -2xe^x dx
=0 + [2xe^x][-1, 1] - ∫[-1, 1] 2e^x dx
=2e - (-2e^(-1)) - [2e^x][-1, 1]
=2e + 2/e - (2e - 2/e)
=4/e

問6

確率を表にまとめると、

	工場A	工場B	工場C
アクセサリー有	0.3%	1%	0.8%
アクセサリー無	29.7%	49%	19.2%
計	30%	50%	20%

確率を求めると、
0.3/(0.3+1+0.8)=1/7

問7

y=(10-3x)/4を代入して、
x^2+y^2=x^2+(100-60x+9x^2)/16
=(25x^2-60x+100)/16
=25/16×(x^2+12/5x+4)
=25/16×((x-6/5)^2+4-36/25)
≧25/16×64/25
=4

問8

ア、イの手前のループではユークリッドの互除法により最大公約数を求めている。
アではaとbが互いに素か(最大公約数が1か)を判定しているので、j=1が正しい。
次のイでは、一方が偶数で他方が奇数であることを判定しているため、(ab)mod2=0が正しい。
ちなみに、(ab)mod2=0ではabともに偶数の場合も条件を満たしてしまうが、その場合はアの部分でjが1にならないため、問題ない。
(ここらへんは非常に分かりにくく作っていると思います)

問9

X, Yは一様分布なので、X=(1/5, 1), Y=(1/4, 1)で囲まれる面積を求めると、
(1-1/5)×(1-1/4)=3/5
X>1/3かつY>1/3の範囲で囲まれる面積を求めると、
(1-1/3)×(1-1/3)=4/9
よって答えは
(3/5-4/9)/(3/5)=1-4/9×5/3
=7/27

問10

速度をx方向とy方向に分解して、
初期：
　v_x=1/2×v_0
　v_y=√3/2×v_0
壁にぶつかった直後：
　v_x=1/2×v_0×e
　v_y=√3/2×v_0
床で跳ね返った直後：
　v_x=1/2×v_0×e
　v_y=√3/2×v_0×e
よって速さはv=ev_0

問11

色々試してみたが、解き方が分からなかったのでパス。
棒の重心or半球殻との接点のどこかを中心にしてモーメントの式を立てるのだと思うが、
aがどのように絡むのかが分からなかった。

問12

AC間の距離を求めると2√3/3、バネ係数をkとし、点Cでの鉛直方向の力の釣り合いを考えると、
mg=1/2×k(2√3/3-1)+1/2×k(2√3/3-1)
=k(2√3/3-1)　－①
同様に、鉛直にして吊るした場合の力の釣り合いは、糸の伸びをxとして、
mg=kx　－②
①、②より、
x=(2√3/3-1)
≒(2×1.732/3-1)
≒0.155
となったが・・・一番回答に近いのが14cm。
これは合っているのか・・・？

問13

失った位置エネルギー+失った運動エネルギー=摩擦力が行った仕事　より、
Fl=1/2×mv^2+mg×l/2　－①
次に、物体に与えた運動エネルギー=増加する位置エネルギー+摩擦力が行った仕事
より、求める速度をv'とすると、
1/2×mv'^2=mg×l/2+Fl
①の結果を代入して、
1/2×mv'^2=mg×l/2+1/2×mv^2+mg×l/2
=1/2×mv^2+mgl
v'=√(v^2+2gl)

問14

この気体を30℃上昇させるのに必要なエネルギーは
3(mol)×30(K)×29.4(J/mol・K)=2.646×10^3J
温度が300K→330Kになることで、体積は1.1倍になる。
このとき、気体が外部に対して行った仕事は、
1.0×10^5(N/m^2)×24.6×10^-3(m^3)×(1.1-1)×3
=0.738×10^3J
よって、内部に蓄えられたエネルギーは
2.646×10^3-0.738×10^3≒1.9×10^3J

問15

壁に向かって4m/sで動くことで、音叉から直接観測点に届く音の速度は336m/sに、壁に反射する音の速度は344m/sになる。
うねりは振動数の差から生じるため、
344/340×440-336/340×440
≒10回
・・・だと思うのだが、合っているのだろうか？

問16

回答の通り。
まずイとウから考えた上でアを考えると分かりやすい。

問17

半径rの球状導体の表面積は4πr^2で、電荷は表面上に一様に分布しているため、
V=Q/4πε_0r^2
また、Q=CVより、
C=4πε_0r^2

問18

電流の大きさはE_i/6.0
力の釣り合いを考えて、
0.1×10=0.5×E_i/6.0×0.3
E_i=40(V)
また、2本のレールに生じる電位差は、
V_0=0.5×0.3×2.0=0.3(V)

問19

回路全体の抵抗をxΩとする。
問題文より、繰り返し単位を１つ増やしても抵抗は変わらないので、
a─┬[2Ω]┐
　[4Ω]　　[xΩ]
b─┴──┘
上記のa, b間の抵抗がxΩになる。
1/x=1/4+1/(2+x)
x=2

問20

回路図を書き直すと
┌──[4Ω]──-┬──[6Ω]──┐
│　　　　　　　　　　[G]　　　　　　　　　│
├[RΩ]┬[6Ω]┬┴┬[9Ω]┬[XΩ]┤
│　　　 └[6Ω]┘　　└[9Ω]┘　　　│
R=8を代入し、抵抗を整理して、
┌[4Ω]-┬[6Ω]────┐
│　　　　[G]　　　　　　　　　│
├[11Ω]┴[9/2Ω]─[XΩ]┤
│　　　　　　　 　　　　　　　 │
Gに電流が流れないため、
11×6=4×(9/2+X)
66=18+4X
X=12

問26

蒸気圧降下により、沸点が上がり凝固点が下がる(はず)ため、5を選択。

問28

六角柱の中に炭素原子は2つあるため、六角柱の質量は
12/N_A×2
体積は
1/2×a×√3a/2×6×b
=3√3/2×a^2b
密度は
(24/N_A)/(3√3/2×a^2b)
=16√3/3N_Aa^2b

問29

電池１
ZnSO4の濃度が均一な方向に動くため、左側ではZn(2+) + 2e-→Zn、右側ではZn→Zn(2+) + 2e-の反応が起こる
よって右から左に電子が流れ、電流は左から右に流れる。
電池２
こちらはよく分からなかったので、適当に選んだ。

問30

それぞれの溶解度積は
[Ag+][C^-]=2.0×10^-10　－①
[Ag+]^2[CrO4(2-)]=2.0×10^-12　－②
また、初期状態で[Cl-]=[CrO4(2-)]=1.0×10^-2のため、
①では[Ag+]=10^-8
②では[Ag+]=10^-5
まで溶解が許容される(はず)。そのため、析出するのはAgClから。
また、Ag2CrO4が沈殿し始めるとき、[Ag+]=10^-5となっているはずだから、
[C^-]=1.4×10^-5

問32

右下の説明を読み、なんとなく理解した内容で、Bの200℃のところとCの1の２点を結ぶ直線の延長上にあるAのメモリを読み取って55℃。
違うかもしれない。

問33

ア：
　蒸留水で濡れていた場合、水溶液の濃度が変わってしまうのでNG。
イ：
　目盛りを読み取って31.4mL。滴定開始時のビュレットの目盛りが5.00mLなので、滴定量は26.4mL
ウ：
　ビュレット洗浄後は乾かす必要あり。

問36

A+(-A)B=A+Bである。
-(AC+B(-C))=(-A)(-C)・(-B)Cであり、(-A)C+(-B)(-C)とは異なる。
例えば、A=1, B=0, C=1の時に結果が異なる。
(A+B)(A+(-B))=Aである。
(A+B)((-A)+C)=A(-A)+AC+(-A)B+BC=AC+(-A)Bである。

問38

地道に計算しても良いが、5を２進数に直すと101となる。
1→10→100(x→x^2→x^4)で乗算２回、100+1(x^4×x)で乗算１回、合計３回となる。
同様に7を２進数に直して111、よって1→10→100(x→x^2→x^4)で乗算２回、100+10+1(x^4×x^2×x)で乗算２回、合計４回
同様に11を２進数に直すと1011となるので、乗算３回＋乗算２回＝乗算５回
18を２進数に直すと10010、乗算４回＋乗算１回＝乗算５回

問40

作業を図に表すと、
A|　　　├─────┤6(8)
B|　　　　　　　　　├─────┤6(12)
C|　　　├───┤4(6)
D|　　　├─┤2(4)
E|├─┤2
F|├─┤2
最も所要時間を短くするためには、作業Bの所要時間を半分にする。
このときの全体の所要時間は9になる。

問47

コンデンサの静電容量はC=εS/d
電圧一定の場合、静電エネルギーはCV^2のため、比誘電率が増加すると静電エネルギーは増加する。
誘導体を挿入した結果エネルギーが上昇するため、そのぶんの仕事を何らかの形でする必要がある。
そのため導体を挿入する方向と反対の方向に力が働く。

問91

10以上の場合はEを表示するため、gが表示されるのは2～7、9～15の場合。
これをまとめると、1---/001-/010-/0110の４通り。
これを更に集約すると回答が導出される。

問92

1. メモリへのアクセスが連続していた方が、先読みによりキャッシュがより有効に働く。
2. キャッシュはメモリの内容をコピーするためのものであり、容量を拡張するためのものではない。
3. キャッシュの記憶容量は１次＜２次＜３次というのが一般的。
4. ヒットした際のアクセス時間が同じであれば、セットアソシアティブ方式の方がヒット率は高くなり平均アクセス時間は短くなる。
5. ウェイ数を増やすと、ヒットした際に見なければならない範囲が増えるため、アクセス時間は長くなる。

問93

リセット信号は負論理なので、クロックが1もしくはリセットが0の際にデータが更新される。
また、リセットが0の際にはQに定数が入り、そうでない場合はクロックによる更新のためQにはDの値が入る。

問94

回路図より、
next Q1 = Q3
next Q2 = Q1 xor Q3
next Q3 = Q2
となる。
あとは地道に出力の値を追っていく。

	Q1	Q2	Q3=A
初期値	1	0	0
1	0	1	0
2	0	0	1
3	1	1	0
4	0	1	1
5	1	1	1
6	1	0	1

問95

オペランドの関係により、 命令K→命令K+2、命令K+2→命令K+3の順序で実行を行う必要がある。
フォワーディング無しの場合：

CLK	IF	ID	OF	EX	WB
1	K
2	K+1	K
3	K+2	K+1	K
4	K+3	K+2	K+1	K
5	K+3	K+2	(K+2)	K+1	K
6		K+3	K+2	-	K+1
7		K+3	(K+3)	K+2	-
8		K+3	(K+3)	-	K+2
9			K+3	-	-
10				K+3	-
11					K+3

フォワーディング有りの場合：

CLK	IF	ID	OF	EX	WB
1	K
2	K+1	K
3	K+2	K+1	K
4	K+3	K+2	K+1	K
5		K+3	K+2	K+1	K
6			K+3	K+2	K+1
7				K+3	K+2
8					K+3

問96

状態遷移図を作成する。

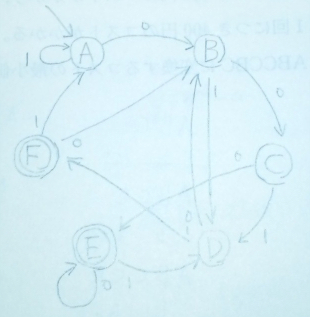
問97

ABC
↓重複操作(300円)
ABCC
↓重複操作(300円)
ABCCC
↓重複操作(300円)
ABCCCC
↓置換操作(400円)
ABCCBC
もしくは、
ABC
↓重複操作(300円)
ABCC
↓重複操作(300円)
ABCCC
↓置換操作(400円)
ABCBC
↓重複操作(300円)
ABCCBC
文字数の関係上、３回の重複操作は必須。また、重複操作だけでは目的の文字列は生成できないので、最低１回の置換操作が必要となる。

問98

y=x^2-aのx切片が√aとなる。
上の式を微分して、y'=2x。
曲線上の点(x1, x1^2-a)における接線の式は以下の通り。
y=2x1(x-x1)+x1^2-a
=2x1x-x1^2-a
x切片を求めると、
x_next=x1/2+a/(2x1)
詳細については、ニュートン法を参照。

問99

n=pq=77
またφ(n)=60
7d≡1(mod60)
選択肢の中から選んでd=43

問100

外部からの入力の際に入力値にコマンドを埋め込み、不正にデータを操作することができてしまう。
詳細はSQLインジェクションを参照。

午後：基礎試験問題

問1

1. 良い学校への進学が一体何になるんだというムードが子供たちの世界に広がったのは
　 経済のグローバル化や長期化する不景気が原因ではない。
2. 学校が職業の準備・予備教育の場という考え方は最近の考え方。
3. 最後の文章より、平等社会での教育は自己実現や貢献の喜びを味わうために学ぶと書かれている。

問2

1. 文章より、内言は後天的に覚えた言語を聞きなれた自分の自分の声の記憶をもとに操られると書かれている。
2. 内言に集中することによって聴覚が働かなくなると書かれている。
3. 内なる声に限らず、外界からの音声を拾うための行為も含まれる。
4. 最後の段落を参照。
5. 啓示体験が責任ある任務として位置づけられるとは書かれていない。

問3

まず5.は選択肢から外れる。
残りを吟味し、2.か4.かで迷った末、2.を選択した。

問4

1.は最初の文章から違うと分かる。
あとは時間が無かったため、残りから適当に選んだ。

問5

時間がなかったため、適当に選んだ。

問6

時間がなかったため、適当に選んだ。

問7

時間がなかったため、適当に選んだ。

問8

時間がなかったため、適当に選んだ。

問9

ウの予想は全て外れているため、BEGHは４位以内に含まれていない。
イの予想のうちBは４位以内に含まれていないため、DFIが４位以内に含まれる。
エの予想のうち、DとFはどちらも４位以内に含まれているため、Cは４位以内に含まれていない。
アの予想のうち、CとEは４位以内に含まれていないため、AとDが４位以内に含まれている。
かつ、ウの予想よりDは3位ではないため、Aが2位。
エの予想のうち、２位はAなので、Dが２位は有り得ない。よってFが３位。
よって順位は一位より(DorI),A,F,(DorI)となる。
この結果を元に選択肢から適切なものを選ぶ。

問10

学活と音楽はどちらも5時限目にあり、かつ音楽の授業のある日は連続していないため、音楽は月５、学活は金５であることが分かる。
国語と算数が１時間ずつ減ることから、残る５コマの内訳は国語、算数、理科、理科、社会。
総合と図工と体育以外は、１日に２時間以上ある日はないため、水４には理科以外は来ないことが分かる。
また国語は月曜、火曜、金曜は既に国語が入っているため、国語は木４に入る。
また、月曜には社会、金曜には算数が入らない。
以上をまとめると以下の表の通り。

	月	火	水	木	金
1	道徳	総合	社会	音楽	体育
2	国語	総合	国語	算数	算数
3	社会	国語	算数	理科	国語
4	算数or理科	算数or理科or社会	理科	国語	理科or社会
給食
5	音楽	体育		図工	学活
6		体育		図工

理科のある水・木は変更後も理科があるため、Bは正しい準備をしていることが分かる。
7月1日が・・・
月曜の場合、算数を準備したAが間違っていたことになる。月４は理科となり、Cは正しい準備をしている。
火曜の場合、Bは正しい準備をしてきたため火４が理科となる。その場合、AC共に誤った準備をしてきたことになってしまう。
水曜の場合、時間割には変更が無いためおかしなことになる。
木曜の場合、算数も理科も音楽も時間割には含まれているため、おかしなことになる。
金曜の場合、通常の時間割に音楽が無いため、Cが音楽を準備するのはおかしい。

問11

問題文の内容を元に以下のような表を作成する。

	A	B	C	D	E	F
Aの本	イタリア	2	4	3	1	5
Bの本	3	タイ	5	2	4	1
Cの本	4	3	トルコ	1	5	2
Dの本	5	1	3	アメリカ	2	4
Eの本	2	4	1	5	フランス	3
Fの本	1	5	2	4	3	エジプト

1～5までの数字は、同じ行、同じ列には１つしか存在しないことを活用する。
数独に近い感覚で解答を導き出せるはず。

問12

以下のような表を作成する。

試合	対戦	控え
1	AB vs CE	D
2	BC vs AD	E
3	DE vs AC	B
4	AE vs BD	C
5	BE vs CD	A

考え方として、まず1試合目と2・3試合目の左側が確定する。
同じペアが2度試合をすることはないため、3試合目でDEと対戦したペアはACであることが分かる。

問13

2枚のカードの合計が、残り1枚のカードと等しくなる組み合わせは以下の4通りのみ。

ケース	組み合わせ
1	1-2-3
2	1-3-4
3	1-4-5
4	2-3-5

1. 例えば、ケース3の場合、Aの持っていたカードが4でもAは自分のカードの数字を知ることができる。
2. 例えば、ケース1の場合、Aの持っていたカードが3でもAは自分のカードの数字を知ることができる。
3. Aのカードが5だとすると、考えられるのはケース3もしくはケース4。
　 いずれの場合でも、考えられる組み合わせが2通り存在するため、Aは自分のカードを知ることができない。
4. ケース3では3のカードを誰も持っていないが、Aのカードが1もしくは4であれば自分のカードを知ることができる。
5. ケース2、ケース3では誰かが4のカードを持っている。

問14

それぞれの頂点について、図を作成して軌跡を求める。

問15

直円錐が8回転して元に戻るため、展開図を作成した際の側面の扇形の角度はπ/4。
底面の周囲と側面の弧の長さが同じことから、側面の扇形の半径は4R。
表面積を求めると、
π/8×(4R)^2+π(R/2)^2=9πR^2/4
なのだが、計算ミスをしてしまった。

問16

三角形BCDに注目する。
図を平面座標に置き換え、直線BGとDFの交点を求めると、DP:PF=4:1となるため、
△BPF=△BCD×1/2×4/5
=2/5×△BCD

問17

大きい正方形の面積は6。
三平方の定理より、小さい正方形２つの面積の合計は6。
中央の直角三角形の面積は1。
左下の直角三角形は中央の直角三角形と合同であるため、面積は1。
これらの合計が14となるため、答えは1～3に絞られる。
残りの中から勘で選んだ。

問18

先手のプレイヤーが１枚カードをめくった状態が
　☆？？？？？
もう1枚めくって柄が異なる確率は4/5。
　☆△？？？？
後手のプレイヤーが１枚めくった時、それが☆or△である確率は1/2。
仮に☆をめくったとして、残りのカードは
　△？？？
後手のプレイヤーが再度１枚めくったとき、それが△である確率は1/3。
この時、残りのカードも後手のプレイヤーが取る。
この場合の確率は4/5×1/2×1/3=2/15　－①
残りのカードが
　△？？？
の状態で、１枚めくったとき、それが●である確率は2/3。
もう１枚カードをめくるとき、それも同様に●である確率は1/2。
この場合の確率は4/5×1/2×2/3×1/2=2/15　－②
　☆△？？？？
の状態で、後手のプレイヤーが１枚めくったとき、それが●である確率は1/2。
再度１枚めくったとき、それが●である確率は1/3。
残りのカードは
　☆△？？
となるため、どちらをめくっても全てのカードをめくることができる。
この場合の確率は4/5×1/2×1/3=2/15　－③
①+②+③=2/5

問19

牛1頭が食べる量をx、1日1アールの土地から生える量をyとすると、
30アール/(2x-30y)=30日
60アール/(2x-60y)=180日
2つの式を連立して、
x=5/6
y=2/90
4頭の牛を100アールの土地に放した場合、
100アール/(4x-100y)
=100/(10/3-20/9)
=90

問20

黒い２マスおよびその間のマスは必ず立方体に含まれる。
中段右のマスが立方体に含まれる場合、上段から１マス、下段から１マス選ぶ方法があるので、4×4=16通り。
上段右のマスが立方体に含まれる場合、その隣のマスも立方体に含まれる。
このとき下段のマスは3通りの選び方がある。
下段右のマスが立方体に含まれる場合は上段に含まれる場合と同じ。
16+3+3=22通り。

問21

１回目のカードを引き終わった時点で、BとDは0点だったので、どちらもハートもしくはダイヤの同じ数のカードを引いたことがわかる。
またAとCはどちらもスペードを引いたことが分かる。
Aが9点なので、BとDの引いたカードはそれぞれダイヤとハートであることが分かる。
このとき、Cは自分で3点のカードを引いたことになるため、Cの引いたカードはスペードの3。
スペードの3はもう使えないので、Aが9点となる組み合わせは1+4+4のみ。
次に２回目のカードを引き終わった時点で、BとDにそれぞれ6点と5点入っているため、BとDはスペードを引き、
AとCはそれぞれダイヤとハートを引いたことが分かる。
残るスペードは2と4しかない。またダイヤとハートの4は使われているため、Dがスペードの2を引き、Cがハートの3を引いたことが分かる。
それぞれのプレイヤーが引いたカードは以下の通り。

回数	A	B	C	D
1	スペード1	ダイヤ4	スペード3	ハート4
2	ハート2	スペード4	ハート3	スペード2

問22

1回転目：10πmm
　・
　・
　・
1800回転目：82πmm
これを全て足しあわせれば良いから、
(10π+82π)×1800/2≒260m

問23

時間が無かったので、粗い計算でなんとなく求めた。ちなみに、
1. 2010年の夫婦のみ世帯数:10688、1975年:3880なので2倍以上。
2. 1980年:15222、1985年:15603で増加している。
4. 2010年:3226、1975年:1390で2倍以上。
5. 高齢者世帯の増加数:8517、核家族世帯の増加数:9504

問24

上の問題と同様に、粗い計算でなんとなく求めたが間違っていた。

	A	B	C	D	E
GDP(億ドル)	43,830	30,324	25,931	27,990	140,108
公的教育支出のGDP比	3.4	4.3	4.9	5.1	5.2
一人あたりGDP	34,000	40,000	40,000	46,000	46,000
公的教育支出(億ドル)	1,490	1,303	1,270	1,427	7,285
人口	128,911,764	75,810,000	64,827,500	60,847,826	304,582,608
一人あたり公的教育支出	11,560	17,200	19,600	23,460	23,920

問25

時間がなかったため、適当に選んだ。

問26

時間がなかったため、適当に選んだ。

問27

時間がなかったため、適当に選んだ。

問28

2.は正しいと思ったので選択した。ちなみに、
3. 生殖行動に限らずフェロモンは分泌され利用されている
4. 植物の葉が緑色に見えるのは、緑色の光を反射しているから。

問29

時間がなかったため、適当に選んだ。

問30

時間がなかったため、適当に選んだ。

---