巨大数の基本Wiki

乗算・冪乗・超冪(テトレーション)など、各種の演算について

最終更新：2021年11月01日 18:51

googoloeasy

- view

管理者のみ編集可

　このページでは、巨大数を作ったり理解したりするのに必要な、最低限の計算方法について解説します。
　以下、aは実数、bは1以上の整数とします。

演算子

　演算子とは、演算、すなわち計算を行う際に、どのように計算したり値を示したりするのかということの指標となる記号のことです。例を挙げると、＋, －, ×, ÷, √ などです。演算は計算とほぼ同じ意味です。

乗算(掛け算)

　乗算(掛け算)は同じ数を何回か足す計算です。つまり、 $a \times b=a+a+ \cdots +a \text{(b copies of a)}$ 　です。
(註："b copies of a"とは、「b個のa」という意味です。このwikiでは数式の表示に日本語が使えないので、英語で書いています。)

　掛け算(乗算)の演算子は、「×」「*」「・」です。手書きでは×と・がよく使われ、インターネット上では*が比較的多く使われます。

　掛け算は、次のように定義することもできます。
　 $a \times b=a+a \times(b-1)$ 　
　このように、何かを、それ自身を使って定義することを「再帰的な定義」といいます。

　掛け算そのものが巨大数を作るのに使われることはあまりありませんが、冪乗や超冪などの基礎になっているので、極めて重要な計算であると言えます。

補足：負の数同士の掛け算はなぜ正の数になるか

冪乗(べきじょう)

　冪乗は聞いたことがない人もいるかもしれないので、すこし詳しく説明します。
　冪乗という言葉は少々難しいですが、「3の2乗」とか「2の10乗」という言葉を聞いたことがある人はたくさんいるでしょう。

　冪乗とは、同じ数を何回か掛ける計算です。つまり、 $a^b=a \times a \times \cdots \times a \text{(b copies of a)}$ です。このとき、aを&(てい){底}、bを指数といいます。
　 $a^b$ は、「aのbじょう」と読みます。記号^(キャレット)を用いて、a^bと書いても同じ意味です。
　クヌースの矢印表記では、 $a \uparrow b$ となります。

　冪乗を再帰的に定義すると、以下のようになります。
$a^b=a$ $\text{ , if b=1}$
$a^b=a \times (a \times \cdots \times a )\qquad \text{ ((b-1) copies of a)}$ $\text{ , if b \geq 1}$

<注意！>
　冪乗の指数が縦に積み重なった場合には、一番上の数字から順に計算していきます。底から計算してはいけません(底から計算するならば、底とその指数に括弧をつけなければなりません)。
　たとえば、 $2^{2^3}$ は、先に指数の $2^3$ を計算し、 $2^{2^3}=2^8=256$ と算出します。これを底から計算すると、
$2^2=4$ なので、与式は $4^3=64$ となり、ぜんぜん違う数値になってしまいます。底から計算するならば、括弧をつけましょう( $(2^2)^3$ といった具合に)。

　また、

は、「3の3の3の3じょうじょうじょう(3の3の3の3乗乗乗)」と読みます。「3の3乗の3乗の3乗」と読むと、ちがう演算になってしまいますので注意してください。

補足：0乗はなぜ1なのか

超冪(ちょうべき) / テトレーション

　超冪は、巨大数以外ではあまり耳にしない概念であると思います。
　超冪はテトレーション(tetration)とも呼ばれる演算方法で、冪乗を何回か繰り返すことです。つまり、

　テトレーションは、冪乗を何回繰り返すか定める数(超冪指数。ここでは、b)を左上において表します。そのほか、クヌースの矢印表記では、 $a \uparrow \uparrow b$ 、コンウェイのチェーン表記では、 $a \rightarrow b \rightarrow 2$ と表記します。

　テトレーションを再帰的に定義すると、以下のようになります。

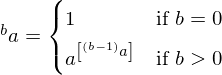
　なお、超冪は、テトレーション以上の超冪乗全般を意味する語としても用いられます。

ペンテーション(超超冪)以上

　ペンテーション(超超冪)は、テトレーションの繰り返しです。もはや意味がわかりません。
　ペンテーションは、クヌースの矢印表記では $a \uparrow \uparrow \uparrow b$ 、コンウェイのチェーン表記では $a \rightarrow b \rightarrow 3$ と表記します。