降下矢印表記 - 巨大数の基本Wiki

　ここでは、私が考案、開発した巨大数の生成方法である、降下矢印表記について解説していきます。
　必要な知識は、指数と対数、およびクヌースの矢印表記です。

降下矢印表記とは

概要

　降下矢印表記とは、私が開発した巨大数の作成法シリーズの総称です。クヌースの矢印表記に基づいて、巨大数を生成します。
　今のところ、緩降下矢印表記(かんこうかやじるしひょうき)、降下矢印表記(こうかやじるしひょうき)、急降下矢印表記(きゅうこうかやじるしひょうき)、墜落矢印表記(ついらくやじるしひょうき)の4つがあります。後ろになるにつれて、増加速度が劇的に上昇します。

(復習)

　クヌースの矢印表記について、念のため復習しておきましょう。かなり簡単な説明なので、詳しく知りたい方はクヌースの矢印表記のページをご覧ください。

　aとbの間にn本の矢印を挟むとき、これを と表記します。
　↑を演算子とする計算を、以下のように定義します(クヌースの矢印表記)。

　例をいくつか挙げます。
例1：3↑0=1
例2：3↑4=81
例3：3↑↑3=3↑3↑3=7625597484987

　クヌースの矢印表記は右結合、すなわち右から計算しなければなりません。

　復習も終わったので、早速降下矢印表記について説明していきます。

緩降下矢印表記

　緩降下矢印表記は、降下矢印表記系統では最も増加速度が小さい表記です。
　正の整数rと、2以上の整数x,yを用いて、以下のように定義されます。

　いくつか例を挙げてみます。
例1：2 ⇓|3|⇓ 1=2³=8
例2：1 ⇓|4|⇓ 3=3⁴=81
例3：2 ⇓|3|⇓ 3=2↑↑↑(3-1) ⇓|3|⇓ (3-1)=2↑↑↑2 ⇓|3|⇓ 2
　　=4 ⇓|3|⇓ 2=4↑↑↑(2-1) ⇓|3|⇓ (2-1)=4 ⇓|3|⇓ 1=4³=64

降下矢印表記

　降下矢印表記は、降下矢印表記系統の中で最初に生まれた表記で、二番目に増加速度が小さいです。
　正の整数rと、2以上の整数x,yを用いて、以下のように定義されます。

　例を挙げましょう。
例1：3 ⇓5⇓ 1=3⁵=243
例2：1 ⇓4⇓ 2=2⁴=16
例3：2 ⇓2⇓ 2=2↑↑2 ⇓2⇓ 1=4 ⇓2⇓ 1=4²=16
例4：2 ⇓2⇓ 3=2↑↑3 ⇓2⇓ 2=16 ⇓2⇓ 2=16↑↑2 ⇓2⇓ 1
　　16↑16 ⇓2⇓ 1=16³²=340282366920938463463374607431768211456
例5：2 ⇓2⇓ 4=2↑↑4 ⇓2⇓ 3=(2↑2↑2↑2) ⇓2⇓ 3=65536 ⇓2⇓ 3
　　=65536↑↑3 ⇓2⇓ 2
　ここで、
　65536⁶⁵⁵³⁶ の常用対数をとると、65536log65536≒315653 であるから、
　65536⁶⁵⁵³⁶≒10³¹⁵⁶⁵³
　よって、
　10³¹⁵⁶⁵³≫log65536 なので、
　ゆえに
　65536↑↑3 ⇓2⇓ 2≒
　

　 について考察する。
　
　この数の常用対数は

　ここで、極めて大雑把な近似を許容し、計算を簡便に行う。

　 であるから、 である(実際の誤差は無量大数などはるかに超えていることに留意されたい)。
　 と簡略して表記すると、
　よって、 である。

　これを与式に代入して、
　
　さらに近似すると
　
　したがって
　 (実際の値はこれより著しく大きい)

　数字を1増やしただけでこの増えようなのですから、yに5を代入したときなど想像もできません。

急降下矢印表記

　急降下矢印表記は、降下矢印表記系統の中では比較的強い表記です。下向き矢印を2本用いて表記します。
　正の整数rと、2以上の整数x,yを用いて、以下のように定義されます。

　降下矢印表記との相違点は、3. の右辺のyが(y+1)になっていることだけです。これが爆発的な違いを生み出します。

　例を挙げますが、1. と2. の例は省略します。

例：2 ⇓⇓2⇓⇓ 2=2↑↑3 ⇓⇓2⇓⇓ 1=16²=256
　これは大したことありません。
例：2 ⇓⇓2⇓⇓ 3=2↑↑4 ⇓⇓2⇓⇓ 2=65536 ⇓⇓2⇓⇓ 2
　　65536↑↑3 ⇓⇓2⇓⇓1≒
　　

墜落矢印表記

　墜落矢印表記は、ここまで紹介したあらゆる降下矢印表記よりも著しく増加する降下矢印表記の系統です。
　正の整数r, y と2以上の整数xを用いて、以下のように定義されます。

　例を挙げます。
例：
例：
　これは

に等しい。

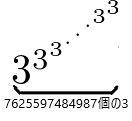
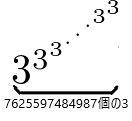
例：
　　
　見やすくするため、 を B と略記する。
　　
　　
　　 ≫ G⁴(2)

註：G⁴(2) はグラハム数という巨大数の計算過程に現れる数であり、その大きさは である。