巨大数の基本Wiki

対数

最終更新：2021年12月03日 17:54

googoloeasy

- view

管理者のみ編集可

　このページでは、巨大数の桁数を測るのに便利な道具である、対数について解説します。
　指数についての知識を前提としているので、指数についてわからない部分がある方は、先に指数と指数表記をご覧ください。
　また、このページでは、特筆ない限り、登場するすべての数は実数です。

対数(たいすう)とは
- 対数の性質
常用対数
演習問題
- 問題篇
- 解答篇

対数(たいすう)とは

　2を3乗すれば、8になります。
　3を4乗すれば、81になります。
　5を6乗すれば、15625になります。

　では、6に何を乗ずれば、216になるでしょうか。

　答えは3です。6³＝6×6×6＝216となります。
　対数というのは、この例での３です。対数という数学らしい言葉を使っているから難しく聞こえるのであって、実のところはそれほど難しい概念ではありません。

　さて、一般的な定義を述べましょう。

　対数(たいすう)(logarithm)とは、 $a^p=M$ が成り立っているときの $p$ のことをいいます。
　正確には、pは、aを底(てい)とするMの対数といいます。また、この $M$ をpの真数(しんすう) といいます。
　pは「aをMにするために必要な乗ずる度合い」であるといえます。

※対数表記において、a>0かつa≠1であり、M>0です。理由は後述します。

　対数pについて、 $p=\log_a{M}$ という表記をします。読みは、「ログaM」です。場合によっては、底は省略される場合があります。logは、対数を意味する英単語logarithmの略です。

　 $a^p=M$ が成り立っているとき、この等式を $p=\log_a{M}$ と操作することを、「(aを底とする)対数をとる」といいます。=M の部分がなくても、「対数を取る」ということができます。

　対数の中でも特に、底を10とする対数を、常用対数といいます。また、底をネイピア数(ネイピア数については、あまり大きくない数を参照してください)とする対数を、自然対数といいます。
　巨大数の世界で登場する対数は、ほとんどが常用対数です。常用対数の底はたいてい省略されるので、巨大数関連で底がない対数を見たときは常用対数である、と思ってもらって大丈夫です。
　以後、このページで出てくる対数は、底が明記されていない限り常用対数とします。

　いくつか対数の例を挙げてみましょう。

例1：2³＝8なので、3は2を底とする8の対数です。
例2：7²＝49なので、2は7を底とする49の対数です。
例3： $4^{-3}=\frac{1}{64}$ なので、-3は4を底とする $\frac{1}{64}$ の対数です。
例4： $\sqrt{5}^2=5$ なので、2は $\sqrt{5}$ を底とする5の対数です。
例5： $8^3=512$ なので、 $3=\log_3{512}$ と表記できます。
例6： $\log_{10}{1000}$ は、10を1000にするために必要な乗ずる度合いを表しているので、すなわち3です。この対数は常用対数です。

<補足：なぜ底と真数に条件があるのか？>
　さきほど、 $a^p=M$ におけるaの条件は、a>0かつa≠1であり、Mの条件(真数条件)は、M>0であると述べました。ここでは、その理由を解説します。

　まずは、底(a)の条件から。
　底が1のとき、1を何乗しても1になります。よって、真数は対数にかかわらず1となり、対数を定める意味がありません。別に底を1としても数学的に支障が出ることはないのですが、意義がないので、底が1である場合は存在しないものとして扱うのがふつうです。
　また、底が0のとき、0を何乗しても0になります(厳密には、0⁰だけは異なります)。よって、底が1の場合と同じく、対数を定める意味がありません。ゆえに底が0である場合は考えません。
　ついでに言うと、0⁰という値は、様々な値をとったり、そもそも何らかの値を取ることができなかったりする(不定)ので、この点でも、底を0とすることには問題があります。詳しくは、指数と指数表記のコラムの欄をご覧ください。
　次に、底が負の数であるときを考えます。底が負の数である場合でも、対数が存在する場合はあります。それは、対数が整数である場合です。たとえば、-4³=-64なので、3は-4を底とする-64の対数です。
　しかし、対数が整数でない場合には、真数が存在しません。たとえば、 $(-2)^{\frac{5}{2}}=X$ という式を考えてみましょう。指数法則から、 $(-3)^{\frac{5}{2}}$ $=\sqrt{-3^5}=\sqrt{-243}$ となるので、 $X=\sqrt{-243}$ といえそうです。
　……しかしながら、 $\sqrt{-243}$ は、2乗すると-243になる数をいいます。そのような数は実数にはありません。 $\sqrt{-243}$ が存在するためには、複素数の真数を許容しなければなりません。これは数学の論理に反していませんが、もはや真数が実数でなくなってしまうので、このページでの真数の条件を満たしません(し、難しくなります)。

　こういった理由から、底は0より大きく、かつ1でない実数としています。

　また、真数が正の値を取る理由についても、前述のことから説明できます。
　底が正の数ならば、真数は複素数である必要があります。たとえば、 $\log_3{(-27)}=x$ とすると、 $3^x=-27$ という等式が成り立つはずですが、これを満たす実数xは存在しません。等式が成り立つには、xは複素数でなければなりません。
　この例からわかるように、底が正であれば、負の真数は存在しえません。
　底が負の数ならば、真数が負になるのは、対数が奇数であるときだけです。たとえば、 $(-2)^3=-8$ という等式では、-8は負の真数となっています。3は-2を底とする-8の対数です。 $(-5)^3=-125$ では、3は-5を底とする-125の対数であって、真数はやはり負の数です。
　しかし、対数が奇数でなければ、実数の真数はありえません。

　以上の理由から、実数の範囲内で対数を扱うときは、a>0かつa≠1、M>0としています。

対数の性質

　対数の定義と指数法則から、以下の対数の性質(対数法則)が成り立ちます。

$1. \qquad \log_a{M}+\log_a{N}=\log_a{MN}$

$3. \qquad \log_a{M^b}=b\log_a{M}$
$4. \qquad \log_a{1}=0$

$6. \qquad a^{\log_a{M}}=M$

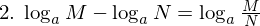
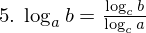
　特に、2. において M=1 ならば、4. より、
$2'. -\log_a{N}=\log_a{\frac{1}{N}}$ が成り立ちます。
　また、5. の変換の公式を、底の変換公式といいます。

補足：対数の性質の証明

常用対数

　前述の通り、常用対数とは底を10とする対数です。
　常用対数は数字の桁数を図ることのほか、地震の大きさの指標であるマグニチュードや、音の単位であるデシベルなどにも用いられています。
　GoogleやYahooなどで"logM"(Mは0より大きい実数で、大きすぎない数。少なくとも10³⁰⁰まではOK)と検索すると、即座に常用対数が出てくるので便利です。

　 $\log{M}=X$ であるとき、Xの整数部分に1を足した数が、Mの桁数になります。たとえば、 $\log{(5443 \times 86677)} = 8.6737 \cdots$ です。8.6737……の整数部分は8なので、5443×86677は9桁です。

覚えておくべき常用対数

　真数が整数である常用対数は、以下の4つの常用対数を覚えておけば導出できます。導出には、先程掲げた対数の性質を用います。
1. $\log{1}=0$
2. $\log{2} \approx 0.30103$
3. $\log{3} \approx 0.47712$
4. $\log{7} \approx 0.84510$

　対数の性質1. によって、 $\log{6}$ が導出できます。
　対数の性質2. によって、 $\log{5}$ が導出できます。
　対数の性質3. によって、 $\log{4}$ と $\log{8}$ と $\log{9}$ が導出できます。

常用対数表

　真数と常用対数の関係を示した表を、常用対数表といいます。常用対数のほとんどすべては無理数なので、常用対数に示された値はほとんどが近似値であることに注意してください。

常用対数を用いた桁数の特定

　常用対数を用いると、一見ではわからない数の桁数を計測することができます。

　 $n \leq \log{M}$ < $n+1$ であるとき、Mは(n+1)桁の数です。たとえば、6<log1468321<7 なので、1468321は7桁の数です。

　累乗で表される数の桁数を、常用対数を使って測ってみましょう。

例： $3^{3^{33}$ (3の3の33乗乗)の桁数を測ります。 $3^{33}=5559060566555523$ ですから、
　　 $3^{3^{33}=$ $3^{5559060566555523}$ となります。
　この数を市販の電卓で計算するのは不可能(CASIOの高精度計算サイトでも「∞」と出ます)なので、これを直接計算して桁数を求めるのは無理そうです。

　ここで、常用対数を使います。 $3^{5559060566555523}$ の常用対数をとると、対数の性質3.から
　 $\log{3^{5559060566555523}}=5559060566555523\log{3}$ となります。
　 $\log{3} \approx 0.47712$ なので、これを代入して計算すると
　 $5559060566555523\log{3} \approx 5559060566555523 \times 0.47712$
　 $\approx 2.652 \times 10^{15}$ となり、 $3^{3^{33}$ は約2652兆桁の数であることがわかります。

註： $3^{3^{33}$ の実際の桁数は、この値とは数千億桁も異なっています。巨大数の世界では、これくらいの誤差は許容範囲です。

　真数があまりにも大きい数であれば、対数をとるときに底は関係なくなります。

例2：

の桁数を求めてみましょう。指数は上から計算するので、まず $3^{3^3}=7625597484987$ であることを利用して、指数部である $3^{3^{3^3}}$ (3の3の3の3乗乗)のおおまかな桁数を求めます。

　 $3^{3^{3^3}}=3^{7625597484987}$ なので、この数の常用対数をとると、 $\log{3^{7625597484987}}$
　すなわち $7625597484987\log{3}$ となります。
　 $\log{3} \approx 0.47712$ なので、これを代入して計算すると
　 $7625597484987\log{3} \approx 3.6383 \times 10^{12}$ (約3兆6383億) となります。よって、
$3^{3^{3^3}}\approx 10^{3.6383 \times 10^{12}}$ (10の3兆6383億乗)となります。

　これを利用して、

の桁数を求めます。

なので、この数の常用対数をとると、

$(10^{3.6383 \times 10^{12})\log{3}$ となります。しかし、 $\log{3}$ はせいぜい1に満たない数なので、これを
$10^{3.6383 \times 10^{12}$ に掛けてもほぼ値は変わりません。よって、
$(10^{3.6383 \times 10^{12})\log{3}$ $\approx 10^{3.6383 \times 10^{12}$ とみなすことができます。ゆえに、

となります。

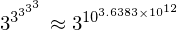
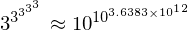
註：この近似値と実際の桁数は著しく離れていますが、やはり近似の範囲内です。無問題。

　一般に、巨大でない数aについて、以下のことがらが成り立ちます。

 において、nが十分大きいならば(目安はn≧100000くらい)、 が成立する。

　これは、言い換えると以下のようになります。

 において、bが十分大きいならば、 の桁数は、おおよそ 桁となる。

常用対数の限界

　常用対数は桁数を測るのに便利な道具ですが、限界はあります。
　著名な例としては、指数タワーが高く積み重なった数の表記です。

　トリトリ(Tritri)という数の桁数を考えてみましょう。トリトリとは、

という巨大数です。クヌースの矢印表記では、3↑↑↑3と書きます。

　トリトリの桁数を、常用対数を用いて表すのは現実的ではありません。先程の節で挙げたことがらを用いて強引に桁数を求めたならば、トリトリの桁数は、(トリトリの3をすべて10にした)桁に近似できるでしょうが、こんなことでは桁数を求めたことにはならないでしょう。
　一応、トリトリの桁数を「近似(註)」して求めるならば、約(トリトリ)桁となりますが、ここに対数の出る幕はありません。蚊帳の外です。

註：この「近似」には無量大数では到底済まないほどの誤差が含まれていますが、トリトリの大きさに比べれば十分小さく、無視できます。

　「では、どのようにして巨大数の桁数を求めればいいのか？」
　こういった疑問が浮かぶかもしれません。

　この問に簡潔に答えると、「桁数を求める術はない」となります。
　もちろん、「巨大数aが十分大きければ、aの桁数はaに近似できる」を使えば、十分大きい巨大数の桁数はその巨大数自身くらい(この「くらい」には無量大数とか不可説不可説転とかを1に近似できるほどの誤差があります)といえるでしょうが、これはナンセンスです。

　いくら対数といっても、快適に使える条件というものがあるわけですね。

演習問題

　演習問題です。対数の習得のためにぜひ解いてみてください。

問題篇

第一問

(1) $x^y=z$ という等式が成り立っているとき、x, y, zをそれぞれ何というか答えよ。
(2) (1)において、x,y,zがすべて実数である場合、xおよびzの範囲を答えよ。
(3) $x^y=z$ という等式を $y=\log_x{z}$ と変形することを何というか答えよ。
(4) 10を底とする対数を何というか答えよ。
(5) ネイピア数e=2.71828......を底とする対数を何というか答えよ。
(6) (4)の対数と真数の関係を示した表を何というか答えよ。

第二問
　log2=0.30103、log3=0.47712、log7=0.84510 とする。指定がなければ、有効数字は4桁。
(1) 本ページで挙げた対数の性質を5つ以上答えよ。
(2) log4 を導出し、値を示せ。
(3) log5 を導出し、値を示せ。
(4) log6 を導出し、値を示せ。
(5) log80 を導出し、値を示せ。
(6) 3⁸⁴ の桁数を示せ。
(7) $999^{999^{999}}$ よりも十分大きい巨大数Xがある。Xの桁数を近似して表わせ。

解答篇

第一問

(1) x：底　y：対数　
(2) x>0かつx≠1　z>0
<解説>
　本ページの補足を参照。
(3) xを底とする対数をとる
(4) 常用対数
(5) 自然対数
<解説>
　自然対数は微積分の領域でよく用いられている。
(6) 常用対数表
<解説>
　常用対数表の数値は小数点以下のあるところ(ほとんどは5桁目)を四捨五入した近似値であることに注意。

第二問
　log2=0.30103、log3=0.47712、log7=0.84510 とする。指定がなければ、有効数字は4桁。
註：本問の解説では、(1)に挙げた対数の性質の番号を用いていることがある。
(1) 以下のうち5つ以上を挙げていれば正解。記号は何でも良いが、範囲を示しておくこと。
$1. \qquad \log_a{M}+\log_a{N}=\log_a{MN}$

$3. \qquad \log_a{M^b}=b\log_a{M}$
$4. \qquad \log_a{1}=0$

$6. \qquad a^{\log_a{M}}=M$
(2) 値：0.6021
<解説>
　log4=log2² であるから、対数の性質3.により
log4=2log2=2×0.30103
=0.60206≒0.6021
(3) 値：0.6990
<解説>
　対数の性質2.を用いる。
$\log{5}=\log{\frac{10}{2}}=\log{10}-\log{2}$
=1-0.30103=0.69897≒0.6990
(4) 値：0.7782
<解説>
　対数の性質1. を用いる。
log6=log(2×3)=log2+log3
=0.30103+0.47712=0.77815≒0.7782
(5) 値：1.9031
<解説>
　まず、log8を算出する。対数の性質3. により
log8=log2³=3log2
=3×0.30103=0.90309≒0.9031
　よって
log80=log(10×8)=log10+log8
1+0.90309=1.90309≒1.9031
(6) 41桁
<解説>
　3⁸⁴ の常用対数をとると
log3⁸⁴=84log3≒40.078
40<84log3<41 であるから、3⁸⁴ の桁数は41桁である。
(7) X
<解説>
　十分大きい巨大数の桁数は、その巨大数自身に近似できる。
　これは以下のように説明できる。

　Xを十分小さい数aと巨大数Tを用いて表すと $X=a^T$ となる。
　両辺に常用対数をとって $\log{X}=T\log{a}$
　ここで、Tは十分大きいので、 $T\log{a} \approx T$ と近似できる。
　よって、 $\log{X} \approx T$
　Xの桁数は、logX+1 だが、1≪logX であるからlogX+1=logX とみなしてよい。
　また、a≪T より、T≒X と近似できる。
　よって、X≒logX+1
　ゆえに、巨大数Xの桁数は、それ自身に近似できる(等しいとみなせる)。

タグ：

対数基礎知識

「対数」をウィキ内検索

添付ファイル

人気記事ランキング

最近更新されたページ

新規Wikiランキング

最近作成されたWikiのアクセスランキングです。見るだけでなく加筆してみよう！

人気Wikiランキング

atwikiでよく見られているWikiのランキングです。新しい情報を発見してみよう！

全体ページランキング

最近アクセスの多かったページランキングです。話題のページを見に行こう！

対数