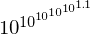管理メニュー

巨大数の基本Wiki

指数と指数表記

最終更新：

googoloeasy

- view
管理者のみ編集可
　このページでは、ある程度までの巨大数の大きさを測るのに便利な道具である、指数について解説します。
　※画像が表示されるまでに少々時間がかかるかもしれません。お待ちください。



指数とは

　指数は乗算・冪乗・超冪(テトレーション)など、各種の演算について でも少し取り上げましたが、冪乗(べきじょう)において、数を何回掛けるか、を表す値です。下に図を示します(aは整数、nは自然数)。

　この図では、aが底(てい)、nが指数です。※掛ける度合い(回数)を指定される数を底(bottom)といいます。

「指数」という語は複数の意味があるので、ここでの指数を特に冪指数(べきしすう)ともいいます。巨大数に使用される指数は、ほとんどが自然数です。
　また、「冪乗」とは、(指数が自然数の範囲では)同じ数を何回も掛ける計算のことと定義されます。
　たとえば、3⁴では、3が底、4が指数(冪指数)です。

　指数が自然数であるときに、以下の指数法則が成り立ちます。aとbは0でない実数、mとnは自然数とします。
\qquad \qquad 1. \quad a^ma^n=a^{m+n}
\qquad \qquad 2. \quad (a^m)^n=a^{mn}}
\qquad \qquad 3. \quad (ab)^m=a^m b^m

　いくつか例を挙げてみます。
  • 法則1の例：3^2 \times 3^3=3^{(2+3)}=3^5=243
  • 法則2の例：(5^2)^3=5^{(2 \times 3)}=5^6=15625
  • 法則3の例：(4 \times 2)^3=4^3 \times 2^3=64 \times 8=512

指数の拡張

　さて、ここまで指数は自然数としてきましたが、指数が自然数でないときを考えてみましょう。たとえば、指数が負の整数であったり、分数であったり、ルートで表される数であったりする場合です。
　そういった場合についても計算ができるようにするため、指数の拡張を行います。

(註)拡張とは
　限られた範囲でしか運用できない法則や規則などを、より広い範囲で運用できるようにすることを拡張といいます。拡張の際には、都合よく定義を改造することがままあります。
　このページでは、自然数の範囲でしか運用できなかった指数を、これから整数や有理数、無理数へと拡張していきます。

　もう一度、指数が自然数であるときに成り立つ指数法則を掲げます(aとbは0でない実数、mとnは自然数)。
\qquad \qquad 1. \quad a^ma^n=a^{m+n}
\qquad \qquad 2. \quad (a^m)^n=a^{mn}}
\qquad \qquad 3. \quad (ab)^m=a^m b^m

整数全体への拡張

　次に、指数が整数全体である場合を考えます(ここから、mとnは整数とします)。このとき、先程掲げた指数法則が成り立つとしますと、法則1から
\qquad \qquad a^m=a^{m+0}=a^ma^0 となるので、0でないどんな実数aに対してもa⁰=1が成り立ちます。
　また、法則2を利用すると、
\qquad \qquad a^ma^{-m}=a^{m+(-m)}=a^0=1 、すなわち a^ma^{-m}=1 が成り立ちます。a≠0としているので、両辺をa^mで割ると(註：割るというのは、逆数を掛けることと同義)、a^{-m}=\frac{1}{a^m} が成り立ちます。

　よって、指数が整数全体であるとき、指数法則が少し変化して以下のようになります。
\qquad \qquad 1. \quad a^ma^n=a^{m+n}
\qquad \qquad 2. \quad (a^m)^n=a^{mn}}
\qquad \qquad 3. \quad (ab)^m=a^m b^m
\qquad \qquad 4. \quad \frac{a^m}{a^n}=a^{m-n



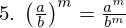
　例をいくつか挙げてみます。
  • 法則1：\qquad 3^4 \times 3^{-5}=3^{4-5}
　　　　 =3^{-1}=\frac{1}{3}
  • 法則2：\qquad (3^2)^{-2}=3^{2 \times (-2)}=3^{-4}=\frac{1}{81}
  • 法則3：(2 \times 3)^{-1}=2^{-1} \times 3^{-1}
　　　　　=\frac{1}{2} \times \frac{1}{3}=\frac{1}{6}
  • 法則4：\frac{3^2}{3^4}=3^{(2-4)}=3^{-2}=\frac{1}{9}

註：この節の始めのほうで、自然数全体でのみ成り立つとしていた指数法則が整数全体でも成り立つと仮定しました。法則を我々にとって都合よくなるように変更したわけですが、変更後も数学の論理には反していないので、問題はありません。

+ 補足：指数をさらに拡張してみよう
　巨大数の指数について理解するには、ここまでの内容で十分です。しかし、数学的好奇心のために、指数を整数よりも広く拡張することを考えてみます。

有理数全体への拡張

　さらに行きましょう。次は指数を有理数全体に拡張します。
復習：有理数 とは、簡単に言うと、整数mと1以上の整数nによって、\frac{m}{n} と表せる数のことです。全ての整数は有理数です。n=1とすれば、整数になることが分かるでしょう。

　ここで、有理数の指数について論じる前に、まずn乗根(エヌじょうこん)の概念を取り入れます。

　簡単に言えば、n乗根はルート(√)の一般化です。
　ルート(平方根)は二乗すると根号内の数になる数のことですね。例えば、\sqrt{3} は二乗すると3になる数を表しています(なお、 \sqrt{3} は無理数です)。

　n乗根は、「n乗すると根号内の数になる数」のことです。nを累乗根といい、累乗根が何なのかは根号の左上に数字をつけて表します。例えば、「3乗すると5になる数」は、 \sqrt[3]{5} と書きます(読みは一通りではありませんが、「5の三乗根」とか「3乗根5」などと読みます)。
　n乗根を正の実数aを用いて表すと、 \sqrt[n]{a} となります。読みは「aのn乗根」または「n乗根a」です。 \sqrt[n]{a} は、n乗するとaになる数を表しています。

　ちなみに：aを負の値に拡張すると、複素数を用いることになりますが、煩雑化を避けるためにここでは取り扱いません。 \sqrt[n]{a} が複素数の範囲であるとき、 \sqrt[n]{a} を満たす複素数はn個存在することがわかっています。

　n乗根について説明し終わったので、いよいよ指数を有理数全体まで拡張しましょう。


　整数全体で成り立っていた指数法則が、有理数全体でも成り立つと考えます。aは正の数、mとnは正の整数とします。このとき、
なので、n乗根の定義から
が成り立ちます。例を挙げて確かめてみましょう。

　例えば、 \Bigl( 5^{\frac{2}{3}} \Bigr) ^3=5^2 です。
　よって、5^{\frac{2}{3}}は、3乗すると5^2になる数ですから、5^{\frac{2}{3}} =\sqrt[3]{5^2}=\sqrt[3]{25} となります。
　ここで、\bigl( \sqrt[3]{25} \bigr)^3=25=5^2 なので、これは正しいことがわかります。

　以上から、指数が有理数であるときに、以下の指数法則が成り立ちます。整数全体とほとんど同じ法則です。aは正の数、mは整数、nは1以上の整数です。

\qquad \qquad 1. \quad a^ma^n=a^{m+n}
\qquad \qquad 2. \quad (a^m)^n=a^{mn}}
\qquad \qquad 3. \quad (ab)^m=a^m b^m
{\Huge \qquad \qquad 4. \quad \frac{a^m}{a^n}=a^{m-n}} =\sqrt[n]{a^m} 
&image(指数1.png)


実数全体、複素数全体への拡張

　ここからは巨大数を作る上でほとんど関係なくなりますが、補足として加えておきます。理解できなければ読み飛ばしてください。

　指数を実数全体まで拡張しましょう。このとき問題になるのは、指数が無理数であるときです。
　無理数は整数mと1以上の整数nによって、\frac{m}{n} と表すことができない数なので、今までに示してきた指数法則を用いることができません。上記の指数法則は、有理数を表すmとnが存在することが条件であるからです。

　そこで、極限(limit)の概念を取り入れ、(無理数)乗を定義します。極限とは、大雑把に言うと、「限りなく特定の値に近づけること」です(厳密には、ε-δ(イプシロンデルタ)理論という数学の理論を使いますが、難しいので取り扱いません)。

　ここでは、とある有理数をとある無理数に限りなく近づけていき、指数が無理数である場合でも指数法則が成り立つようにさせます。
　とある無理数に限りなく近づいた有理数は、その無理数であるといって差し支えありませんが、同時に有理数の性質をも持っています。数学的に厳密な言い方ではありませんが、無理数でありながら有理数として扱ってよいという、都合のいい性質を持っているわけです。

　理論ばかりで具体例がなければ理解は難しいでしょうから、一度具体例を挙げてみます。
　\sqrt{5}は無理数であり、2.2360679774997896964091……と無限に続くことが知られています。ここでは、底を10として、指数が\sqrt{5} になるように(有理数である)指数を\sqrt{5}に近づけていった場合の値を示します。

10^{2}=100
10^{2.2}=158.4893192 \cdots
10^{2.23}=169.8243652 \cdots
10^{2.236}=172.1868574 \cdots
10^{2.2360679774}=172.2138109 \cdots
10^{2.23606797749978969640}=172.2138109 \cdots

　値が一定の値に近づいていくのが分かるでしょうか。指数をさらに\sqrt{5} に極限まで近づけていけば、それは10^{\sqrt{5} の値に等しくなります。結果として、10^{\sqrt{5}\approx 172.2138109{\small \cdots} となると予想できます(この等式は証明できます)。

　以上から、指数が無理数の場合にも、指数が有理数であるときと同じように計算できることがわかりました。ゆえに、指数を実数全体で定義することができます。


　最後に、指数を複素数にまで拡張する場合を考えます。複素数は、実数a, bと虚数単位i (i²=-1)を用いてa+bi と表すことのできる数です。
　極形式で複素数を表すとき、e^{i \theta}=cos \theta +i sin \theta が成り立つことが知られています。

+ コラム：0の0乗の値は？
　註：以下の内容は、極限と指数関数、集合論、およびネイピア数の知識が必要です。わからない部分は調べるか読み飛ばすかしてください。

　ここまで、底は0でない実数としてきました。では、底が0のときの冪乗はどうなるのでしょうか。

　まず、指数が正の数であるときについて考えてみましょう。
　0に何を掛けても0です。よって、指数が0でない実数であるとき、0が底であるならば、その数は指数に関わらず常に0となります。たとえば、0^1=0, \quad 0^{-29}=0, \quad0^{2.4}=0,\quad (0^3)^{-4}=0 といった具合です。

　次に、0の0乗について考えてみましょう。結論から言ってしまえば、0の0乗は複数の値をとりうります。
  • 1になる場合
　指数関数(指数を変数とする関数)のひとつである f(x)=x^x を使います。この関数において、変数xを0に近づけていけば、その値は0⁰に近づいていくことが予想されます。つまり、\lim_{x \to +0}{f(x)}=0^0 となるだろうと考えられるわけです。
　では、実際にグラフを書いてみましょう。Geogebraというソフトで f(x)=x^x を出力したグラフを以下に示します。

　グラフでは、xが0に近づくほど、f(x)の値が1に近づいていることがわかります。つまり、\lim_{x \to +0}{f(x)}=1 であることがわかります。
　よって、0^0=1 となります。

　この方法のほかにも、0^0=1 とすることがあります。
　例えば、指数関数の定義式や、二項定理の公式を簡便にする場合です。こういった場合では、便宜上 0^0=1 としたほうが綺麗になるので、そのように定義することが多いです。

　また、集合論では、0^0 は空集合から空集合への写像(空写像)の個数とされます。空写像は1つしかないので、0^0=1 となります。
  • 0になる場合

　指数関数g(x)=0^x を考えます。xが0に限りなく近づくとき(x>0 とします)、g(x)の値は0⁰に限りなく近づいていきます。つまり、\lim_{x \to +0}{g(x)}=0^0 になるだろうと考えられるわけです。
　0に0でない実数を乗じれば、必ず0になるというのは先程述べたとおりです。\lim_{x \to +0}{g(x)} におけるxは、0に限りなく近くはありますが、0ではありません。よって、\lim_{x \to +0}{g(x)}=\lim_{x \to +0}{0^x}=0 となります。
　ゆえに、0^0=0 となります。

  • 定められない場合
　そもそも、0⁰の値は定められない(不定)である、ということもできます。指数を整数全体に拡張するときの考え方を振り返ると、その理由が分かります。
　指数が自然数のとき成り立つ指数法則を、整数全体で成り立つと仮定したとき、aが0でない実数である場合、
a^{(m+0)}=a^m+a^0 という等式が成り立つので、a^0=1 であると定められるのでした。
　では、aが0であったらどうなるでしょうか。このとき、
0^{m+0}=0^m+0^0 となるでしょう。
　m≠0なので、0^m=0^{m+0}=0 です。よって、
0^{m+0}=0^m+0^0
\Leftrightarrow 0=0 \times0^0 となります。この等式の両辺を0で割って、0^0=1

……とするわけには参りません。なぜならば、0で割るという行為は、現代数学で定義されていないためです(詳しくは、あまり大きくない数を参照ください)。よしんばこの等式が成り立つとしても、0に何を掛けても0になるので、0^0はどんな値でもよいことになってしまい、値は定められません(不定)。

　このように、0^0 の値については、数学的にも決まった答えがなく、立場によっていろいろな値をとったり、値が定義されなかったりします。

指数表記と指数タワー

指数表記とは

　純粋な炭素の塊12.012gに含まれる炭素原子の個数は、約602214000000000000000000個です。その炭素原子を回っている電子一個の質量は、およそ0.00000000000000000000000000000090194gです。
　また、観測可能な宇宙の全質量は、一説では30000000000000000000000000000000000000000000000000000kgであり、観測可能な宇宙に存在する原子の総量は
100000000000000000000000000000000000000000000000000000000000000000000000000000000個程度であるとされています。
　このような0が多く連なった極めて大きな(小さな)数を書くのは面倒ですし、0の数を書き間違える可能性もありますし、視認性にも欠けます。

　そういった数を簡便に表すには、指数表記という表記法が便利です。指数表記は、以下のように表されます。
a \times 10^n 　ただし、1≦a<10であり、かつnは整数です。aを仮数部、nを指数部と呼びます。aが1の場合、省略される場合があります。
　指数表記を使えば、ながーく続く0の個数を、指数部の数で表すことができます。先程あげた数量を、指数表記で表してみましょう。
  • 12.012gの純粋な炭素に含まれる炭素原子の個数:6.02214×10²³個
  • 電子一個の質量:9.0194 \times 10^{-31} \text{g}
  • 観測可能な宇宙の質量:約3.0×10⁵²kg
  • 観測可能な宇宙に存在する原子の個数:約1.0×10⁸⁰個

　正の数では、最も位が大きい数を除いた数字の桁数が、指数部の数になります。
例：1234000000=1.234×10⁹
　この例では、最も位が大きい1の後に続く234000000の桁数が9なので、指数部が9となっています。

　負の数を指数表記で表すときは、指数部を負の整数にします。
例：0.0032=3.2 \times 10^{-3}

　指数部は、小数点以下に続く0の個数に1を足した数にマイナスをつける、と覚えれば簡単です。

　いくつか、身近な巨大数を指数表記で表してみましょう。

  • 成人の血管をすべて繋ぎ合わせたおよその長さ：100000000m=1.0×10⁸m (1億m)
  • 世界人口(2021年)：約7875000000人=約7.875×10⁹人 (約78億7500万人)
  • 小麦の収穫量(2019年)：約765760000000kg=約7.6576×10¹¹kg (約7657億6000万kg)
  • 地球上の全生物の総重量(概算値)：1100000000000トン=1.1×10¹²トン (1兆1000億トン)
  • 日本の実質GDP(2019年, 概算値)：554400000000000円=5.544×10¹⁵円 (554兆4000億円)
  • スーパーコンピューター京における、1秒あたりの浮動小数点演算可能回数(FLOP)：10000000000000000回=1.0×10¹⁶回 (1京回)
  • 2021年現在、地球上の国家で印刷された最も大きい数の紙幣：100000000000000000ペンゲー紙幣=1.0×10²¹ペンゲー紙幣 (10垓)　※ペンゲーは、ハンガリーのかつての通貨です。
  • 地球の質量(おおよその値)： 5972400000000000000000000kg=5.9724×10²⁴kg (5杼9724垓kg)
  • ジョーカーを除くトランプ52枚を並べる場合の数：52!≒80658175170943880000000000000000000000000000000000000000000000000000通り＝8.065817517094388×10⁶⁷通り (8065不可思議8175那由他1709阿僧祇4388恒河沙通り)
  • 囲碁の場合の数(盤面の駒の状態)：1000000000000000000000000000000000000000000000000000000000000 000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000通り=1.0×10¹⁷⁰通り
  • 囲碁の場合の数(ゲーム木複雑性)：1000000000000000000000000000000000000000000000000000000000000 000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000000000000000000通り=1.0×10⁴⁰⁰通り

指数タワー

　確かに、指数表記は大きな数を表記するのに便利です。数十、数百と並ぶゼロを、10の右上に指数部を置くだけで表すことができるのですから。

　しかしながら、指数表記にも限界はあります。あまりにも指数部が大きくなると、指数部の数を把握するのが難しくなってきます。
　その好例として、仏典『大方廣佛華嚴經(だいほうこうぶつげごんきょう)』に出てくる中で最大の数の単位、不可説不可説転(ふかせつふかせつてん)を挙げましょう。
　不可説不可説転は、10^{37218383881977644441306597687849648128} です。
　指数部の数が何なのか、ぱっと見て判断できましたでしょうか。京や垓は超えているけれど、詳しくはわからない、という方が多いでしょう。
　不可説不可説転の指数部を単位をつけて表すと、10の37潤(かん)2183溝(こう)8388穣(じょう)1977秭(じょ)6444垓(がい)4130京6597兆6878億4964万8128乗となりますが、これでも大きすぎてうまく把握できないでしょう。

　このような指数部が大きすぎる数の表記に、指数タワーを用います。指数タワーとは、指数部を指数表記で表し、塔(タワー)のように数を表記することです。先ほどの不可説不可説転を指数タワーで表すと、概数で 10^{3.7218 \times {10^{37}} となり、すっきりした姿になります。

計算

　指数タワーの計算は、右上から行います。
ただしい例：
=3^{3^{27}}=3^{7625597484987}
\approx 10^{3.638 \times 10^{12}}

誤った例(左下から計算した)：
=27^{3^3}=19683^3
=7625597484987

　また、
は「3の3の3の3乗乗乗」と読みます。これは、「 [3の{3の(3の3乗)乗} 乗]」であると考えると理解できるでしょう。
　なお、3乗の3乗の3乗の3、と読むと、上記の誤った例を表します。

指数タワーの具体例


　指数タワーで表される数に身近なものはほぼありません。単純に大きすぎるためです。
　指数タワーで表される数をいくらか挙げてみます。

  • 1個の栗まんじゅうにバイバインをかけ、1000年放置した場合の栗まんじゅうの個数(理論上)：2^{105189120} \approx 10^{31665080.8} \approx 10^{3.17 \times 10^{7}(個)
  • アボガドロ数のアボガドロ数乗の概算値：10^{1.4320501 \times 10^{25}}
  • SCP-1941 に登場する巨大数：2^{2{^{79}}+ 3^{2^{83}}+ 5^{2^{89}}+ 7^{2^{97}} \approx 10^{1.33911 \times 10^{29}}
  • 不可説不可説転(概数)：10^{3.7218 \times {10^{37}}
  • トンネル効果によって、全ての物質がブラックホールになるまでにかかる時間：10^{10^{26}} - 10^{10^{76}} (時間の単位は何でも構わない)
  • 物理学的偶然によって、熱的死に至った宇宙で初期宇宙並のエネルギーが発生するまでにかかる時間：
    (時間の単位は何でも構わない)
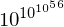
  • この世に存在する様々な宇宙の、そのすべての質量を一つのブラックホールに変換して一つの箱に詰め込み、そのブラックホールが蒸発してなくなり、それからポアンカレの回帰定理に従って再びブラックホールが生まれるまでにかかると予想される時間：
    (宇宙論で使われた最大の数)


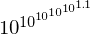
　もはや想像のつかない数ばかりですね。

指数タワーの先へ

　指数タワーによって表記される数は、異常に大きいものとなります。しかし、指数タワーにも限界はあります。
　現実的に考えて、指数タワーの段数には限りがあるためです。段数は、せいぜい積み重ねたところで10段くらいが限界と言えるでしょう。

　では、巨大数はここで限界を迎えるのでしょうか？

　否。

　巨大数の世界には、指数タワーで表示できる数すらチリクズと化すほど、大きい数を作れる表記方法が存在します。
　たとえば、クヌースの矢印表記やコンウェイのチェーン表記といったものです。

　指数タワーのその先を見てみましょう。指数タワーは、巨大数の世界の入り口に過ぎないのです。




演習問題


　最後に演習問題を用意しました。指数を身につけるために解いてみてください。

問題篇

第一問

(1) 冪乗における指数とは何か、簡潔に説明せよ。この問での指数は自然数に限る。

(2) 指数という語を(1)での意味に限定する意味で、特に何というか。

(3) 指数が自然数のときに成り立つ指数法則を3つ示せ。

(4) 指数が整数のときに、(3)で示すべきものに加えて成り立つ指数法則を2つ示せ。

(5) 0⁰の値を求めよ。ただ一つに求められないならば、とりうる値を一つ示せ。値が全く求められないならば、「不定」と記せ。

(6) 指数を積み重ねる表記法を答えよ。

第二問
(1)～(6)および(8)では、示された式を計算せよ。

(1) 3⁴

(2) (3³)²

(3) 4^{-3}

(4) \frac{2^4}{2^2}

(5) (3 \times 6 )^3

(6) \Bigl( \frac{9}{3} \Bigr)^3

(7) \sqrt[3]{4} を3乗した値を答えよ。

(8) 5 ^{\sqrt{2} の値に最も近いものを以下の(甲)～(丁)から選べ。
　(甲) 5 ^{1.400} \qquad (乙) 5^{1.420}\qquad (丙) 5 ^{1.410}\qquad　(丁) 5 ^{1.415}

第三問
註：万以上の数の単位は、億、兆、京、垓、𥝱、穣、溝、澗、正、載、極、恒河沙、阿僧祇、那由多、不可思議、無量大数　である。単位が一つ上がるごとに、値は1000倍になる。

(1) 指数表記は、1以上の整数a, nを用いてa \times 10^n と表すことができるが、aの値には限りがある。aのとりうる範囲を示せ。

(2) (1)における a および n の名称をそれぞれ答えよ。

(3) 100000000000 を指数表記で示せ。

(4) 123456789101112 を指数表記で示せ。ただし、(1)における a の有効数字は3桁とする。

(5) 0.00000041を指数表記で示せ。

(6) 月の質量は、約734垓6000京kgである。この数値を指数表記で示せ。

(7) 物理学的に意味があるとされる最大の温度であるプランク温度は、約1溝4168穣K(ケルビン)である。プランク温度を指数表記で示せ。

(8) ジョーカーを除くトランプ52枚を一列に並べる順列は、約8066不可思議 通りである。この数値を指数表記で示せ。

(9) 観測可能な宇宙の総エネルギーは、約674無量大数J(ジュール)である。この数値を指数表記で示せ。

(10) アボガドロ数のアボガドロ数乗は、約10^{14320501000000000000000000} である。この数値を指数タワー表記で示せ。

解答篇


+ クリックまたはタップで展開
　まず略解を示し、必要に応じて解説や補足を掲載した。

第一問

(1) 指数とは、ある数を何回掛けるかを示す数である。
<補足>
指数が正でない整数であったり、有理数である場合には、「何回」という言い方ができないので、本問での言い方はできない。

(2) 冪指数

(3)
\qquad \qquad 1. \quad a^ma^n=a^{m+n}
\qquad \qquad 2. \quad (a^m)^n=a^{mn}}
\qquad \qquad 3. \quad (ab)^m=a^m b^m

(4)
\qquad \qquad 4. \quad \frac{a^m}{a^n}=a^{m-n

(5) 実数のいずれかを示せばよい。
<解説>
　0⁰は、モノイド論や集合論では1、極限の考えを用いればあらゆる実数または無限大をとる。指数の拡張の考え方を適用すれば、不定となる。

(6) 指数タワー

第二問

(1) 3⁴=3×3×3×3=81

(2) (3^3)^2 =3^{3\times 2}=3^6=729
<解説>
　ふつうに計算する場合、3を地道に掛けるよりも、3³をまず計算し、27の2乗として計算したほうがよい。

(3) 4^{-3}=\frac{1}{4^3} = \frac{1}{64}
<解説>
　mが整数のとき、a^{-m}=\frac{1}{a^m}が成り立つことを利用する。

(4) \frac{2^4}{2^2} =2^(4-2)=2^2 =4
<解説>
　m, nが整数のとき、\quad \frac{a^m}{a^n}=a^{m-n} が成り立つことを利用する。

(5) (3 \times 6 )^3=3^3 \times 6^3=27 \times 256=6912
<解説>
　m, nが整数のとき、\quad (ab)^m=a^m b^m が成り立つことを利用する。
　ふつうは、( )の中を先に計算したほうがよい。

(6) \Bigl( \frac{9}{3} \Bigr)^3 =3^3=27

(7) 4
<解説>
　n乗根をn乗すると、根号の中の数値になる。

(8) (丁)
<解説>
　\sqrt{2}=1.41421356237 \cdots であるから、(丁)の指数がもっとも\sqrt{2} に近い。

第三問
註：万以上の数の単位は、億、兆、京、垓、𥝱、穣、溝、澗、正、載、極、恒河沙、阿僧祇、那由多、不可思議、無量大数　である。単位が一つ上がるごとに、値は1000倍になる。

(1) 1≦a<10

(2) a:仮数部　n:指数部

(3) (1.0×)１0¹¹
<解説>
　100000000000はすなわち1000億である。1のあとに続く0は11個である。

(4) 1.23×10¹⁴
<解説>
　仮数部の有効数字の指定がなければ、示された数を指数表記で表すと1.23456789101112×10¹⁴となる。しかし実際には仮数部の有効数字は3桁なので、４桁目の4を四捨五入して、仮数部を1.23とする。1のあとに続く数の桁数は14である。

(5) 4.1 \times 10^{-7}
<解説>
　この数は「41」で終わっているので、仮数部は4.1となる。指数部については、小数点以下の数が末端を除いて7個あるので、7とする。

(6) 7.346×10²²(kg)
<解説>
　1京＝10¹⁶、1垓＝10²⁰である。よって、100垓＝10²²<734垓<10²³＝1000垓である。ゆえに、指数部は22となる。

(7) 1.4168×10³²(K)
　1穣＝10²⁸、1溝＝10³²である。

(8) 8.066×10⁶⁷(通り)
<解説>
　1不可思議＝10⁶⁴である。1不可思議＝10⁶⁴<8066不可思議<10000不可思議＝1無量大数＝10⁶⁸であるから、指数部は67となる。

(9) 6.72×10⁷⁰(J)
<解説>
　1無量大数＝10⁶⁸である。1無量大数＝10⁶⁸<672無量大数<1000無量大数＝10⁷¹であるから、指数部は70となる。

(10) 10^{1.4320501 \times 10^{25}}
<解説>
　指数部の桁数は26桁なので、指数部の指数部は25となる。

タグ：

基礎知識 指数 対数
「指数と指数表記」をウィキ内検索
「対数」関連ページ
人気記事ランキング
  1. 乗算・冪乗・超冪(テトレーション)など、各種の演算について
  2. クヌースの矢印表記
もっと見る
最近更新されたページ
もっと見る
ウィキ募集バナー