巨大数の基本Wiki
クヌースの矢印表記
最終更新:
googoloeasy
-
view
このページでは、巨大数を表記するために開発されたクヌースの矢印表記について解説します。指数の知識を前提にしているので、指数が分からない方は先に指数と指数表記のページをご覧ください。冪乗の話も出てきますが、ここで解説するので大丈夫かと思います。
クヌースの矢印表記
概要
クヌースの矢印表記とは、ドナルド=クヌースというアメリカの数学者が1976年に開発した、巨大数の表記方法です。タワー表記ともいいますが、これは和製語です。英語で"Tower Notation " などと言っても通じません。
クヌースの矢印表記では、上向き矢印(↑)を用います。
クヌースの矢印表記を使えば、指数タワー(指数に指数をのせる表記)を用いても表せないような巨大数を簡単に作ることができます。しかしながら、クヌースの矢印表記というのは、実のところ素朴な掛け算や冪乗などの繰り返しです。
クヌースの矢印表記では、上向き矢印(↑)を用います。
クヌースの矢印表記を使えば、指数タワー(指数に指数をのせる表記)を用いても表せないような巨大数を簡単に作ることができます。しかしながら、クヌースの矢印表記というのは、実のところ素朴な掛け算や冪乗などの繰り返しです。
定義
クヌースの矢印表記(以下、矢印表記)は、矢印の本数によって、できる数が全く異なるものになります。
予備知識の解説
まず、矢印表記を理解するために必要な知識を簡単に解説します(詳しい解説は乗算・冪乗・超冪(テトレーション)など、各種の演算についてで述べています)。
この節では、aは実数、nは0以上の整数です。
この節では、aは実数、nは0以上の整数です。
- 足し算の繰り返しは、掛け算になります。
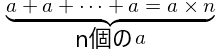
例:3+3+3+3+3=3×5=15
- 掛け算の繰り返しは、
冪乗 になります。
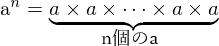
例:3×3×3×3=3⁴=81
- 冪乗の繰り返しは、
超冪 /テトレーション になります。
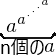
例:
- 超冪の繰り返しは、
ペンテーション (超超冪)になります。
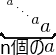
- ペンテーションの繰り返しはヘキセーション、ヘキセーションの繰り返しはセプテーション、セプテーションの繰り返しはオクテーション……と、どんどん続いていきます。
予備知識の解説を終えたので、さっそく矢印表記の解説に入っていきます。以下、aは0でない実数、bは0以上の整数です。
矢印表記は、複数の数字の間に矢印を挟むことによって表記します。↑の代わりに、サーカムフレックス( ^ )を使っても構いません。
矢印表記は、複数の数字の間に矢印を挟むことによって表記します。↑の代わりに、サーカムフレックス( ^ )を使っても構いません。
- 矢印が1本であれば、冪乗を表します。
例:4↑4=4⁴=256
b=0ならば、指数法則から が成り立ちます。
が成り立ちます。
例:3141592653589793238↑0=1
数字が3つ以上になると、指数タワーと同じになります。
例:3↑3↑2=3↑(3²)=3↑9=3⁹=19683
例2:5↑4↑3↑2=5↑4↑(3↑2)=5↑4↑9=5↑(4↑9)=5↑262144
5²⁶²¹⁴⁴≒6.2×10¹⁸³²³⁰
例2:5↑4↑3↑2=5↑4↑(3↑2)=5↑4↑9=5↑(4↑9)=5↑262144
5²⁶²¹⁴⁴≒6.2×10¹⁸³²³⁰
<注意!!>
矢印表記は右結合、すなわち右から計算します。左から計算してはいけません(左から計算する場合には、下矢印表記という別の表記法を用いなければなりません)。
左結合で計算すると、以下の誤った例のように、非常に小さな数が出てきます。
矢印表記は右結合、すなわち右から計算します。左から計算してはいけません(左から計算する場合には、下矢印表記という別の表記法を用いなければなりません)。
左結合で計算すると、以下の誤った例のように、非常に小さな数が出てきます。
誤った例:3↑3↑2=(3↑3)↑2=27↑2=729
誤った例2:4↑4↑4=256↑4=4294967296
註:正しくは、4↑4↑4=4↑256≒1.341×10¹⁵⁴。
誤った例2:4↑4↑4=256↑4=4294967296
註:正しくは、4↑4↑4=4↑256≒1.341×10¹⁵⁴。
- 矢印が2本であれば、超冪(テトレーション)を表します。右結合で計算する点は変わりません。
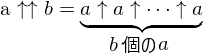
次のように表記することもできます。
例:2↑↑4=2↑2↑2↑2=2↑2↑4=2↑16=65536
例2:2↑↑4=2↑{2↑↑3}=2↑2↑{2↑↑2}=2↑2↑2↑{2↑↑1}
=65536
例3:3↑↑4=3↑3↑3↑3=3↑3↑27=3↑7625597484987
3⁷⁶²⁵⁵⁹⁷⁴⁸⁴⁹⁸⁷≒
例2:2↑↑4=2↑{2↑↑3}=2↑2↑{2↑↑2}=2↑2↑2↑{2↑↑1}
=65536
例3:3↑↑4=3↑3↑3↑3=3↑3↑27=3↑7625597484987
3⁷⁶²⁵⁵⁹⁷⁴⁸⁴⁹⁸⁷≒
矢印が1本のときと同じく、 が成り立ちます。
が成り立ちます。
指数表記が役に立つのは、基本的にテトレーションまでです。
指数表記が役に立つのは、基本的にテトレーションまでです。
宇宙論で使われた最大の数は、10↑↑6より小さいです。この世で起こった、あるいは起こるであろうすべての事象や予想についての数は、すべてテトレーションで現実的に表せると考えて構わないでしょう。
- 矢印が3本であれば、ペンテーション(超超冪)を表します。右結合です。
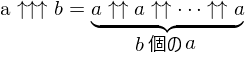
ペンテーション以上になると、極めて大きな数を簡単に叩き出すことができます。
例:2↑↑↑4=2↑↑2↑↑2↑↑2=2↑↑2↑↑(2↑2)
2↑↑2↑↑4=2↑↑(2↑2↑2↑2)=2↑↑65536
=
2↑↑2↑↑4=2↑↑(2↑2↑2↑2)=2↑↑65536
=

例2:3↑↑↑3=3↑↑3↑↑3=3↑↑(3↑3↑3)=3↑↑7625597484987
=
=

例2で挙げた数は、トリトリと呼ばれる有名な巨大数です。
矢印表記の一般化
矢印の本数が多くなると、本数を書き間違えたり、何本の矢印があるのか分かりにくくなってしまいます。
例: (矢印が20本)
(矢印が20本)
こういった大量の矢印も簡潔に表記できるように、矢印表記を簡略化します。
aとbの間にn本の矢印があるとき、これを

aとbの間にn本の矢印があるとき、これを

例えば、3↑↑↑3=3↑³3、10↑↑↑↑10=10↑⁴10 です。
矢印表記は、この表記方法を用いて以下のように定義されます。



3. は、以下のように言い換えることができます。


その他便利な表記、定理など
- クヌースは、↑が使用できない場合には ^ を代用表記として定めました。
- 上矢印を用いて、
と表記することがあります。
例:
括弧の後ろにさらに指数を乗せることもできます。

例:
なお、どのようなnであっても が成り立ちます。
が成り立ちます。
例:2↑⁴⁵⁶⁷2=4
例:2↑⁴⁵⁶⁷2=4
演習問題
演習問題です。
問題篇
第一問
nは自然数。
(1) クヌースの矢印表記は、誰によって、何年に開発されたか。
nは自然数。
(1) クヌースの矢印表記は、誰によって、何年に開発されたか。
(2) クヌースの矢印表記では、ふつう↑を演算子として用いるが、代用表記も認められている。その場合、↑の代わりに何の記号を用いるか。答えよ。
(3) ↑が一本であれば、何の演算を表すか。以下の選択肢から選べ。
(甲) 加算 (乙) 乗算 (丙) 冪乗 (丁) 超冪(テトレーション) (戊) ペンテーション(超超冪) (己) ヘキセーション(極冪) (庚) それ以外
(甲) 加算 (乙) 乗算 (丙) 冪乗 (丁) 超冪(テトレーション) (戊) ペンテーション(超超冪) (己) ヘキセーション(極冪) (庚) それ以外
(4) ↑が二本であれば、何の演算を表すか。(3)の選択肢から選べ。
(5) ↑が三本であれば、何の演算を表すか。(3)の選択肢から選べ。
(6) ↑がn本あるとき、これをどのように略記できるか。
(7) 矢印表記は右結合か、左結合か、答えよ。
(8) 矢印がn本のとき、クヌースの矢印表記を定義せよ。
(9)  を略記して表わせ。
を略記して表わせ。
第二問
(1)~(7)では、与式を計算せよ。指数タワーを用いて表してもよい。指数表記で答える場合、仮数部の有効数字は3桁とする。
(1)~(7)では、与式を計算せよ。指数タワーを用いて表してもよい。指数表記で答える場合、仮数部の有効数字は3桁とする。
(1) 2↑5
(2) 3↑4
(3) 3↑3↑3
(4) 3↑↑3
(5) 4↑↑3
(6) 3↑↑↑3
(7) 2↑↑↑↑↑↑↑↑↑↑↑2
(8) 4↑↑4444444444444と4↑↑↑4 の大小を比較せよ。
(9) 3↑4↑3の答えは531441か。正しければ○と答え、誤っていれば計算過程を明示したうえで、正しい答えを示せ。
解答篇
| + | クリックまたはタップで展開 |
