管理メニュー

俺の勉強支援@Wiki

三角比

最終更新：

oreno_benkyou

- view
だれでも歓迎！ 編集

STEP1:そもそも三角比とは

基本の解説


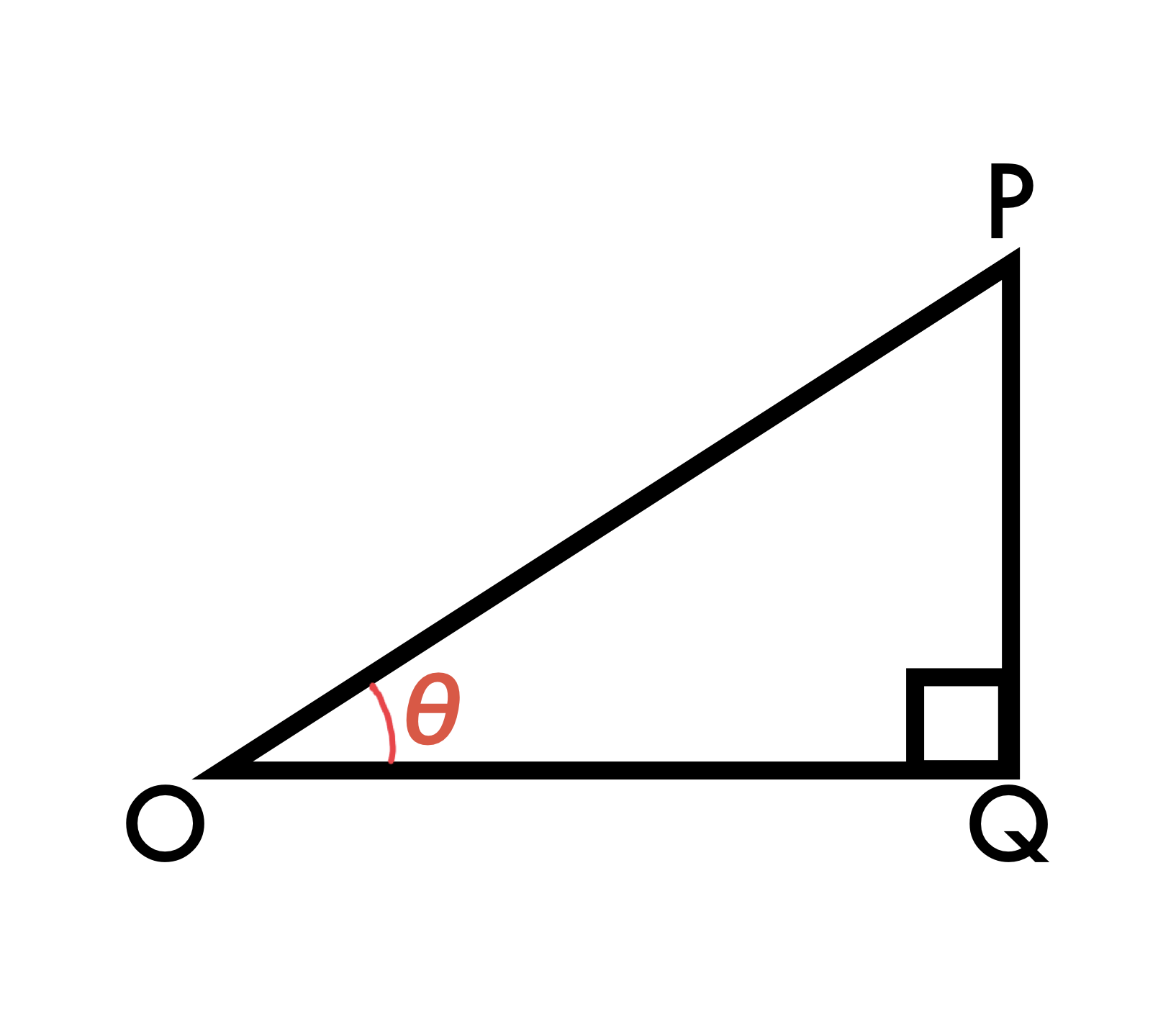
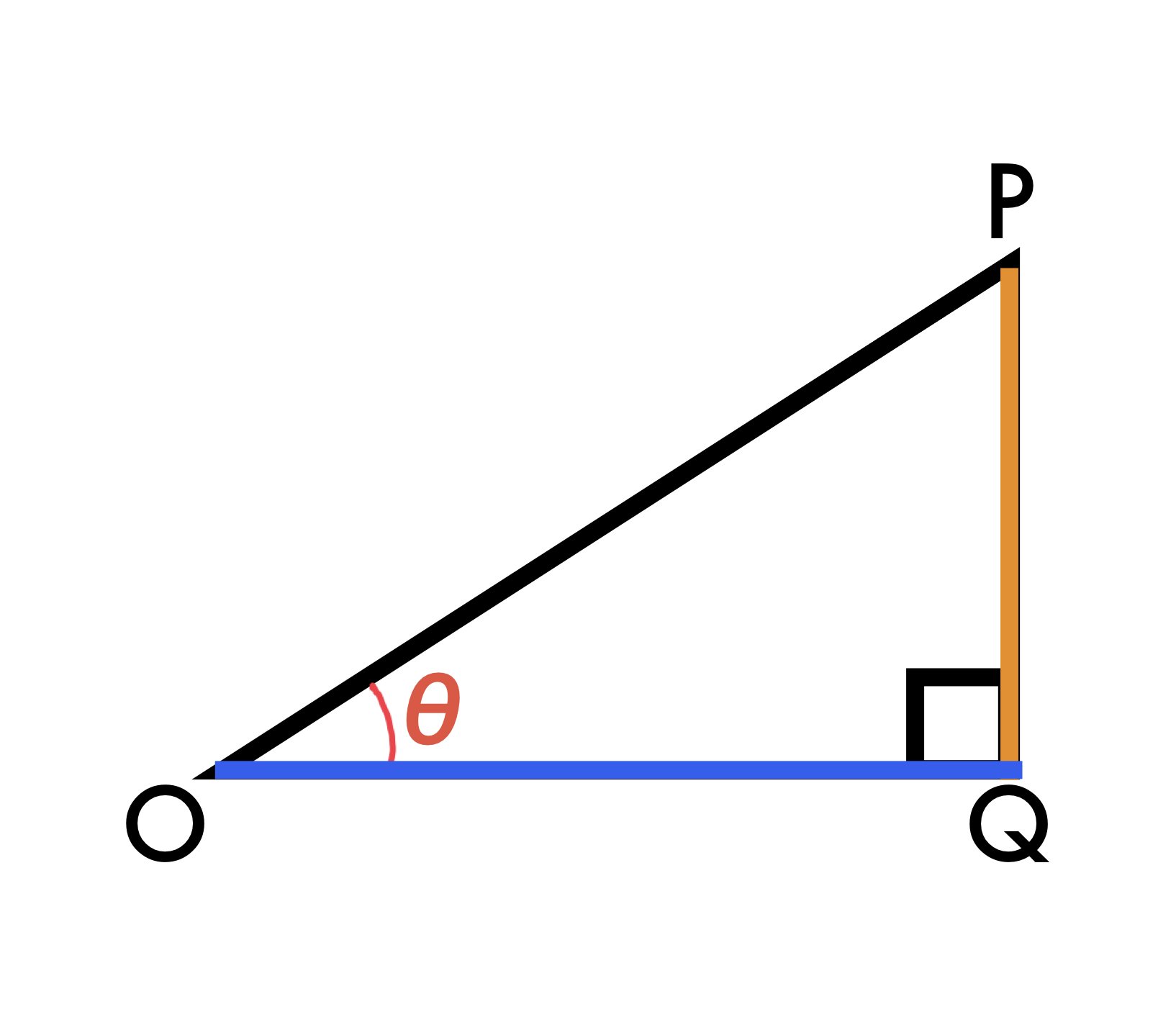
このような三角形、お堅く言うと∠POQが鋭角である直角三角形で
∠POQの大きさをθにすると 
sin\theta =\frac{PQ}{OP}
cos\theta =\frac{OQ}{OP}
tan\theta =\frac{PQ}{OQ}
という式が成り立つのだが、もう少し詳しく見ていこう。

ちなみに、海外では
\frac{sinx}{n}=\frac{si\cancel{n}x}{\cancel{n}}=six=6
というジョークがあるが、そんな式はもちろんないので注意。

sin

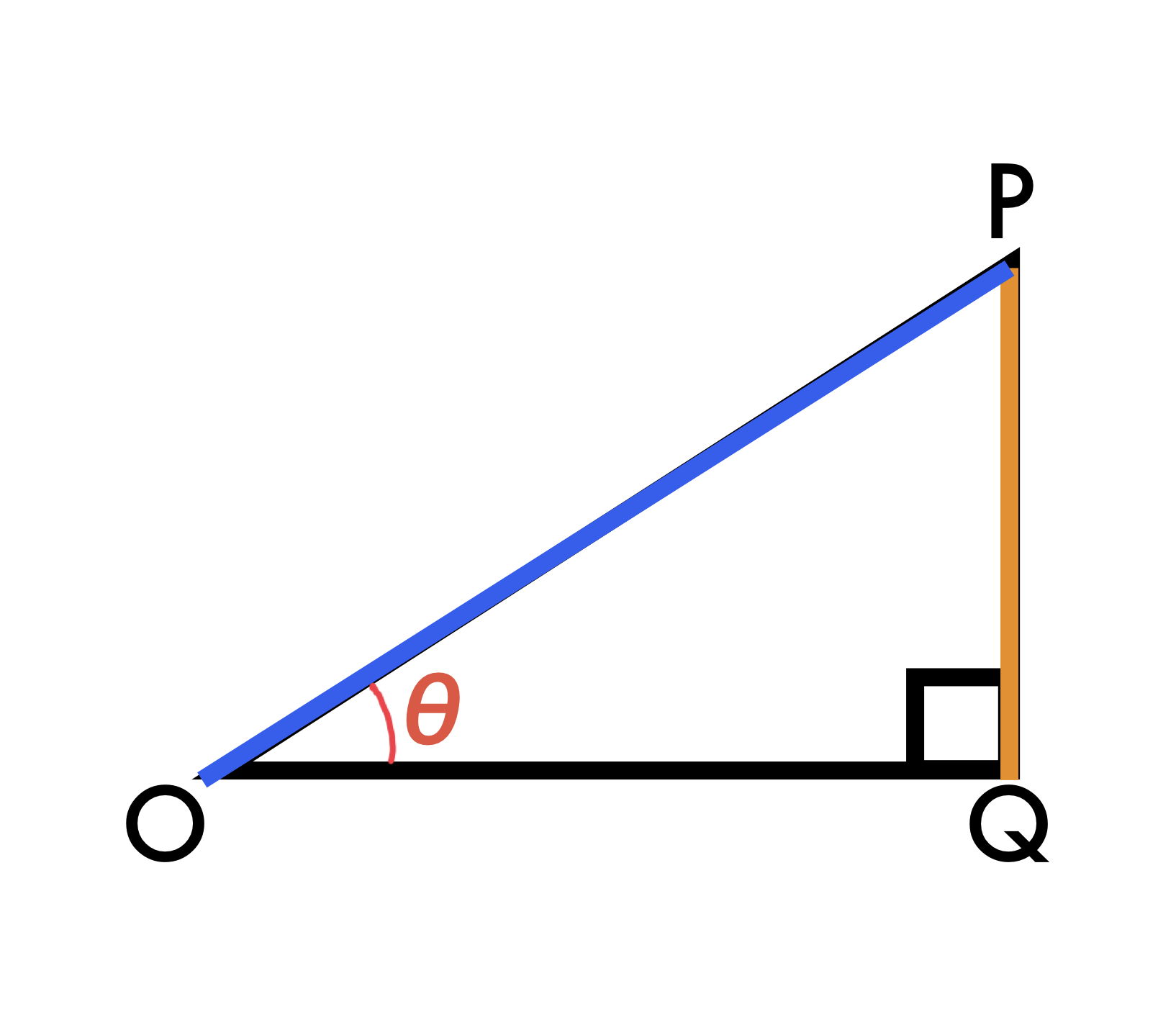
※⬛︎:分子　⬛︎:分母 
sin\theta =\frac{PQ}{OP}
何もない角からθ側(斜辺)が分母、直角側が分子と覚えると良いだろう。

cos

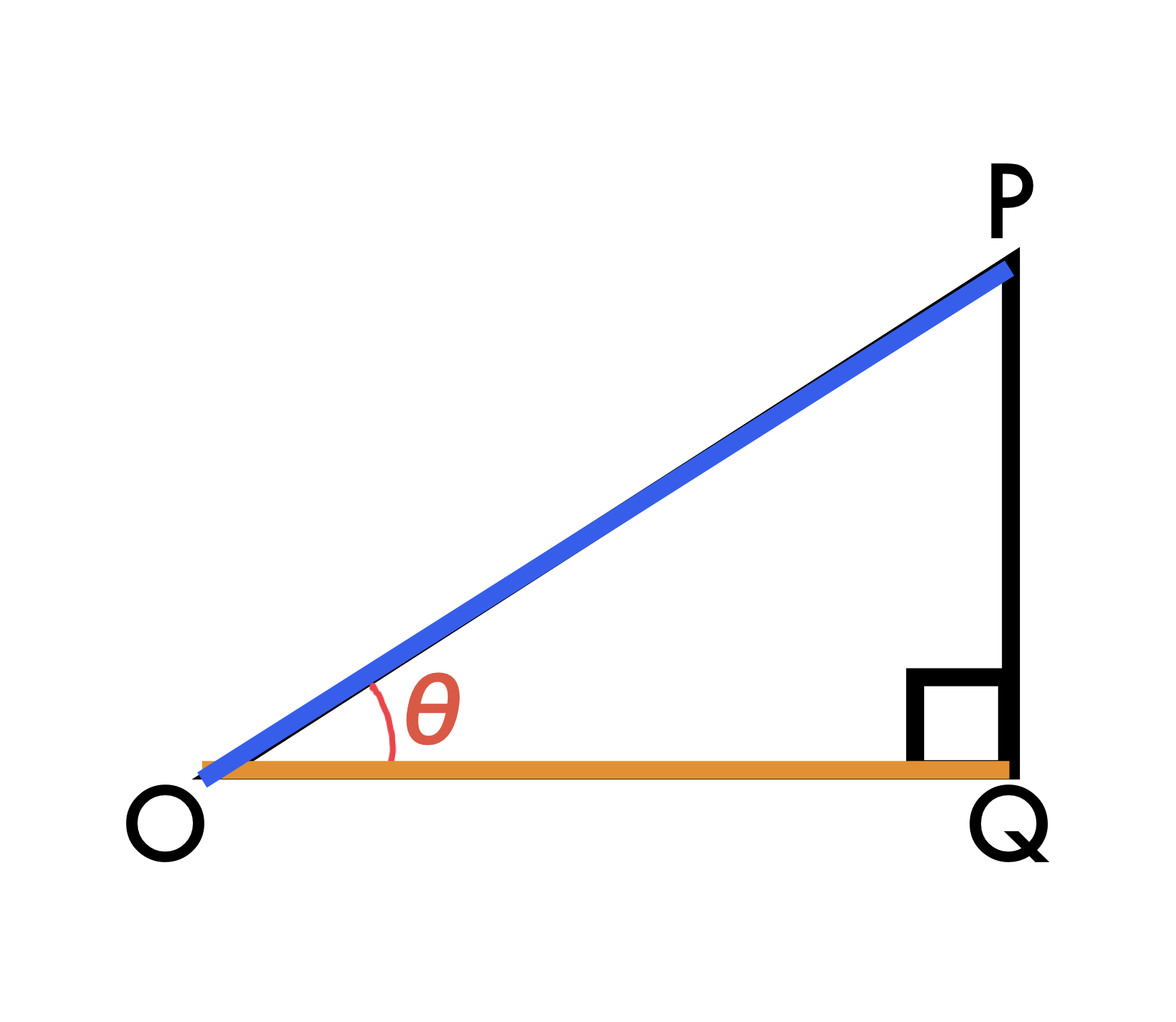
※⬛︎:分子　⬛︎:分母 
cos\theta =\frac{OQ}{OP}
θ角から何もない角側(斜辺)が分母、Θ角から直角側が分子と覚えると良いだろう。

tan

※⬛︎:分子　⬛︎:分母 
tan\theta =\frac{PQ}{OQ}
直角からθ側(cosの分子)が分母、何もない角側(sinの分子)が分子と覚えると良いだろう。

STEP2:三角比の表

基本解説

この世には三角比の表というのがある。

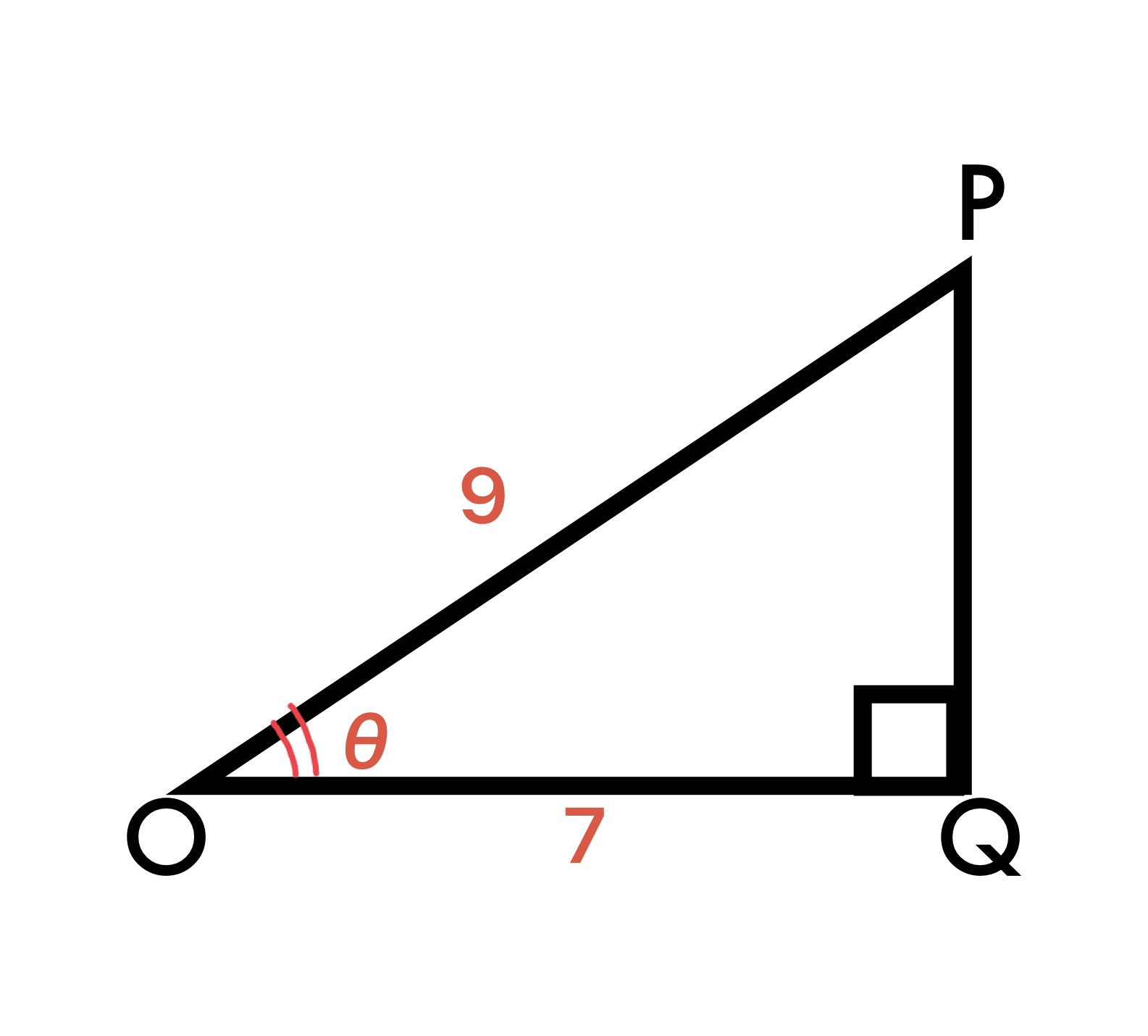
例題1

この三角形のθのおおよその大きさを三角比の表を用いて求めよ。

解説

この問題は深く考えなくても良い。この2つの数で求められるのはcosである。
よってこの三角形のcosは\frac{7}{9}となる。
単純に、\frac{7}{9}のおおよその値を求めると0.7777…となる。ここで三角比の表を見てみよう。
\theta sin\theta cos\theta tan\theta
0° 0.0000 1.0000 0.0000
1° 0.0175 0.9998 0.0175
〜省略〜
38° 0.6157 0.7880 0.7813
39° 0.6293 0.7771 0.8098
40° 0.6428 0.7660 0.8391
今はcosθを求めたいので、見るのはcosの欄。
0.7777…に1番近いのは39°の欄にある0.7771となるはずだ。よって、おおよその大きさは
\theta = 39^\circ
となる。

類題

1 次の式を因数分解せよ。(★☆☆☆☆)

(1)(14a^2b+7ab^2c)
答え
(2)(9a^2bcd+18ab^3d+6c^2d+15a^3b^4c^3d+3a^4bc^2d)
答え

タグ：

+ タグ編集
  • タグ：
タグの更新に失敗しました
エラーが発生しました。ページを更新してください。
ページを更新
「三角比」をウィキ内検索
人気記事ランキング
  1. 執筆メンバーのお誘い
  2. 数学/数Ⅰ/数と式/単項式と次数・係数
  3. 数学/数Ⅰ/三角比/三角比
もっと見る
最近更新されたページ
もっと見る
ウィキ募集バナー