| このページは書きかけです |
|---|
| このページにおける解説・類題などは完全な物ではありません。 編集に協力していただけるメンバーを募集しています。 |
| 詳しくはこちらをご覧ください |
STEP1:そもそも集合って?
基本の解説
まず集合とは、範囲がはっきりした数の集まりを集合と呼ぶ。「8時だョ!全員集合」の略ではない。(*1)(*2)
例えば、Aと呼ばれる集合に1,2,3,4,5,6,7,8,9,10,11,12という数があったとする。
図にするとこうだ。
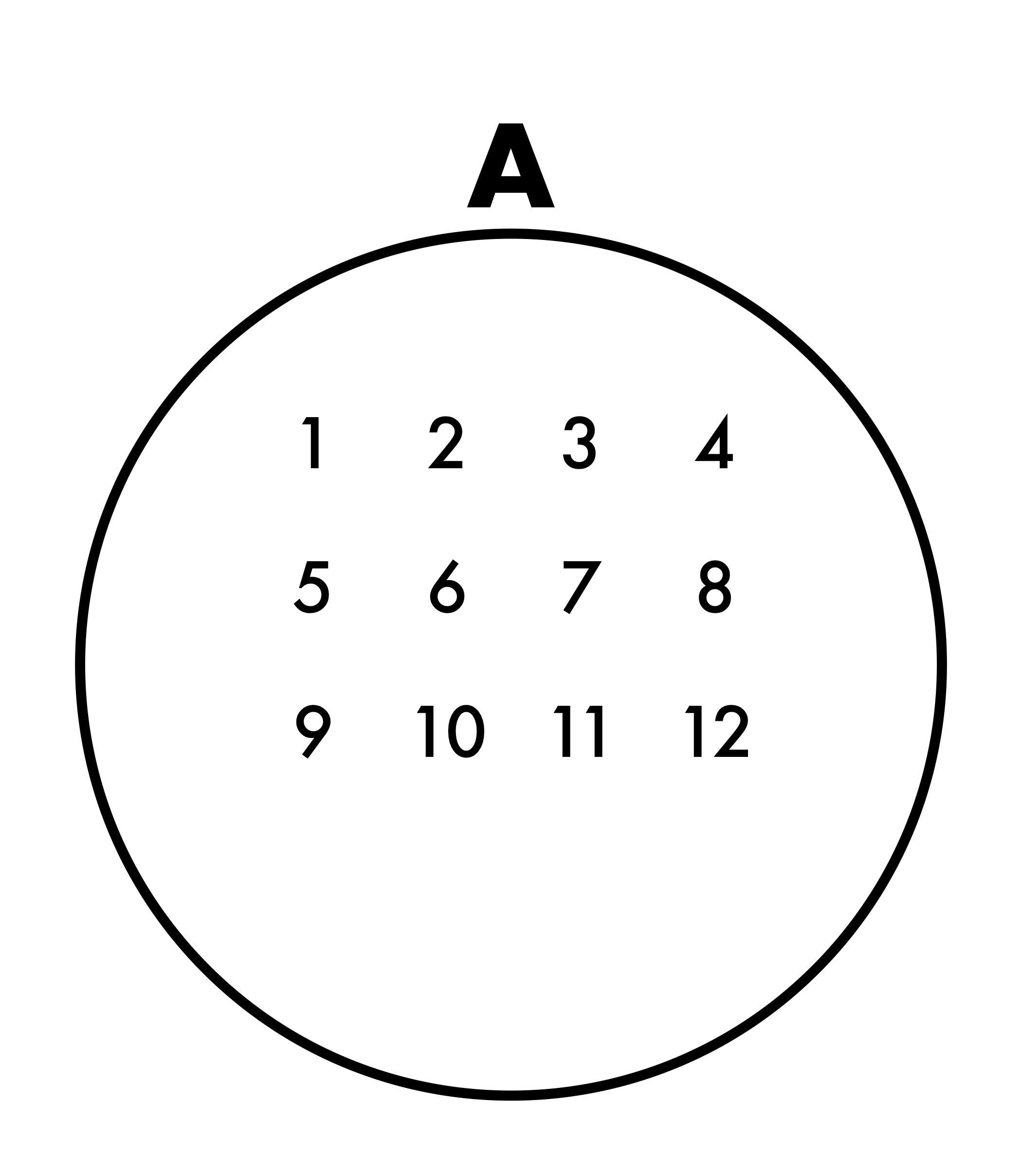
これを数式にすると
例えば、Aと呼ばれる集合に1,2,3,4,5,6,7,8,9,10,11,12という数があったとする。
図にするとこうだ。

これを数式にすると
A={1,2,3,4,5,6,7,8,9,10,11,12}
となる。これの1,2,…などを要素と呼ぶ。
この要素の条件は特定の数字だけではなく、条件式で表すこともある。
例えとして3の倍数でありながら0以上15以下の数の集合とした場合は
この要素の条件は特定の数字だけではなく、条件式で表すこともある。
例えとして3の倍数でありながら0以上15以下の数の集合とした場合は
B={3x|0≦x≦15}
のように表せられる。xが入るわけではないことに注意。
実際Bに入る数は0,3,6,9,12…のようになる。
実際Bに入る数は0,3,6,9,12…のようになる。
例題1
解説
STEP2:集合
今度は、先ほどのA,Bの数をジャンル分けしてみよう。
ジャンル分けといっても、数AにもBにも存在する数とかAにしかない数とかBにしかない数とか、そんな具合の数字たちである。
とりあえずこの二つの数のベン図を用意してみた。
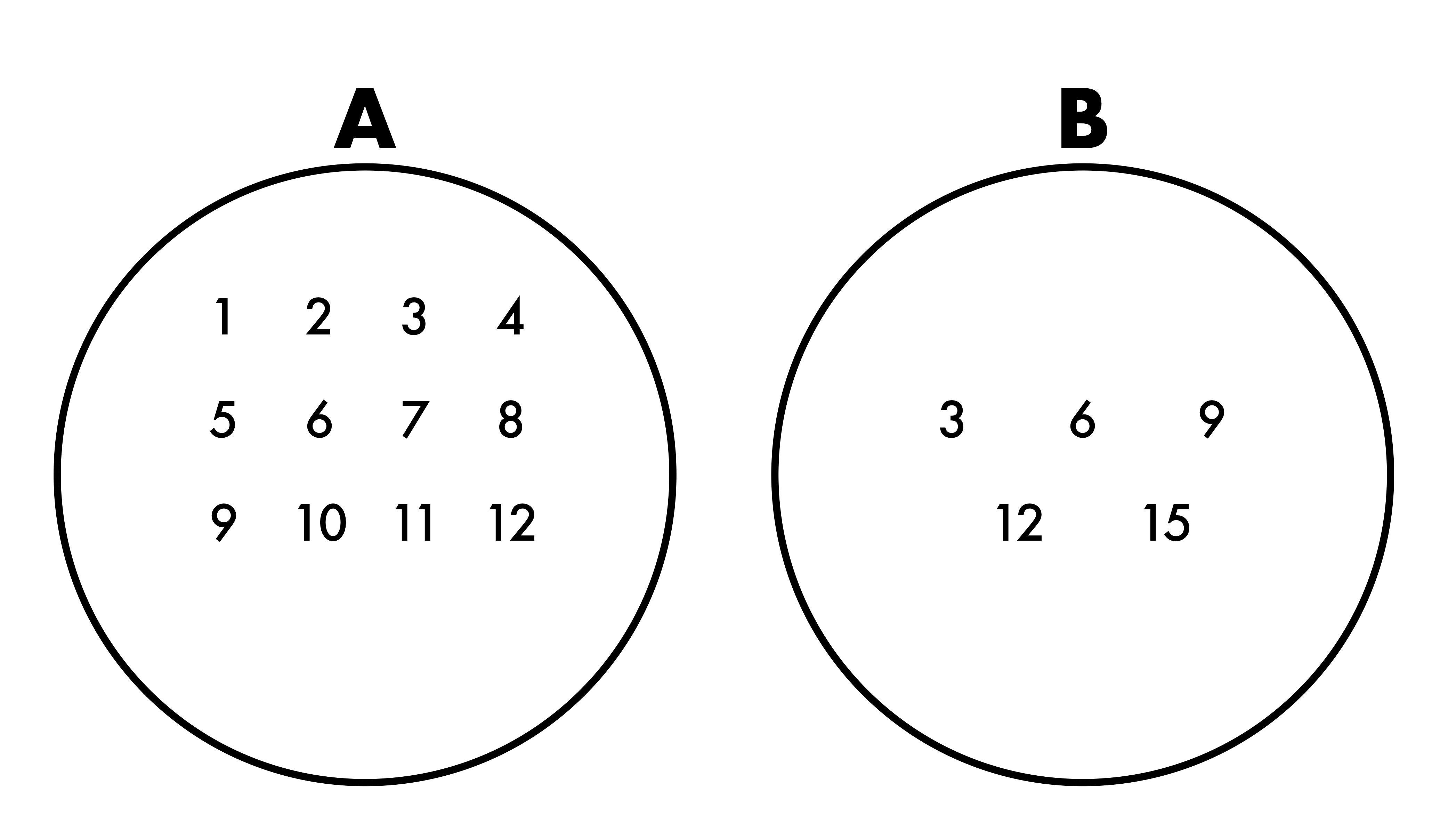
まず、数AにもBにも存在する数を見ていく。
こういうのは表みたいにして炙り出すのが手っ取り早い。
ジャンル分けといっても、数AにもBにも存在する数とかAにしかない数とかBにしかない数とか、そんな具合の数字たちである。
とりあえずこの二つの数のベン図を用意してみた。

まず、数AにもBにも存在する数を見ていく。
こういうのは表みたいにして炙り出すのが手っ取り早い。
| A | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B | 3 | 6 | 9 | 12 | 15 |
見てわかる通り、AとB両方に属する数は{3,6,9,12}となる。
この二つの要素で両方に属する数を、 などと書く。
などと書く。
ベン図はこのようになる。
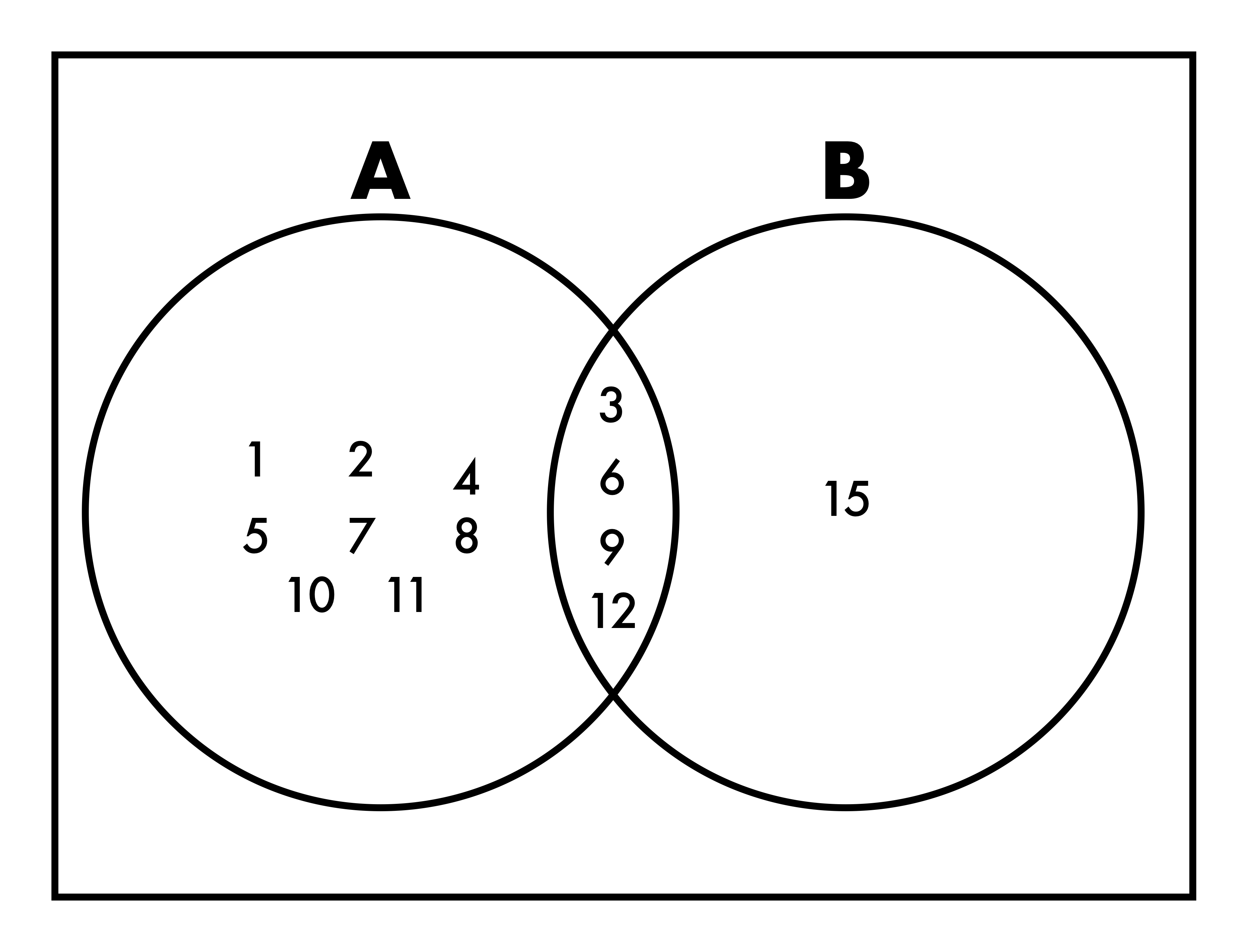
この二つの要素で両方に属する数を、
ベン図はこのようになる。
