※製作中
著者:Ghn.lab
著者:Ghn.lab
三角関数(sin,cos)
三角関数とは?
三角関数(さんかくかんすう、英: trigonometric function)とは、平面三角法における、角度の大きさと線分の長さの関係を記述する関数の族、およびそれらを拡張して得られる関数の総称である。鋭角を扱う場合、三角関数の値は対応する直角三角形の二辺の長さの比(三角比)である。
引用元:Wikipedia
上の説明は気にしなくてもいいです(!?)。簡単に言うと、「半径1の決まった角度においての円周上の座標」です。
ティラミスさんの三角関数の作品を見れば目で分かると思います。
→https://api.programmingzemi.com/contents/U8KifyTBrdkam-7gHHts/landing]
このように、円の右側から反時計回りに○度のところの座標のx,yをcos,sinが表していると思います。
三角関数は、向きから座標を求めるのにとても重宝するブロックとなっています。
ティラミスさんの三角関数の作品を見れば目で分かると思います。
→https://api.programmingzemi.com/contents/U8KifyTBrdkam-7gHHts/landing]
このように、円の右側から反時計回りに○度のところの座標のx,yをcos,sinが表していると思います。
三角関数は、向きから座標を求めるのにとても重宝するブロックとなっています。
三角関数の基本的な公式
sin²θ+cos²θ=1

この式は変数が数字であれば、いつでも1を返す。((半径1の円の中心から円周への直線の長さはいつでも1になるため。)
足される数と足す数が2乗になっているのは、三平方(ピタゴラス)の定理(*1)を利用しているため。
豆知識:sin²θをsinθ²と書いてしまうとsinθの2乗ではなくθを2乗した値のsinになってしまいます…sinやcosは数に比例しません
三角関数を用いたプログラム
中心から円を描く軌道
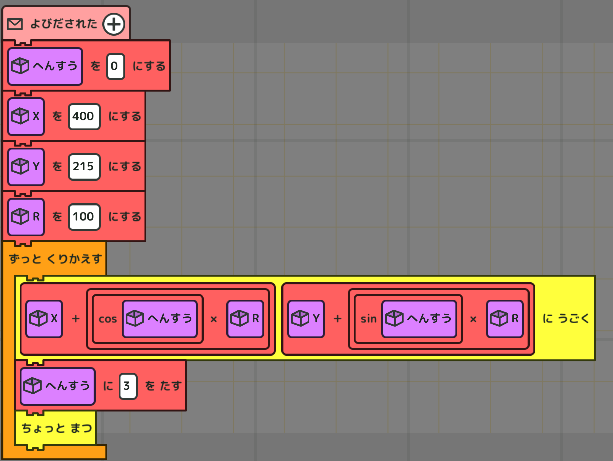
円の中心(横X,縦Y)から半径Rの円を描く。
このプログラムでは、2秒かけて画面の中心で反時計回りに半径100の円を1周する。
逆三角関数(atan2)
逆三角関数とは?
逆三角関数(ぎゃくさんかくかんすう、逆三角函数、英: inverse trigonometric function、時折 cyclometric function[1])は(定義域を適切に制限した)三角関数の逆関数である。具体的には、それらは正弦 (sine)、余弦 (cosine)、正接 (tangent)、余接 (cotangent)、正割 (secant)、余割 (cosecant) 関数の逆関数である。
引用元:Wikipedia
上の説明は気にしなくてもいいです。簡単に言うと、「三角関数の逆バージョン」です。
三角関数は角度から長さなどを求めましたが、逆三角関数では座標から角度を求めるようになっています。
ちなみに今回紹介するatan2では、-180~180を出力します。
三角関数は角度から長さなどを求めましたが、逆三角関数では座標から角度を求めるようになっています。
ちなみに今回紹介するatan2では、-180~180を出力します。
逆三角関数を使ったプログラム
座標に向かって進む
既存のブロック「ちかくの(キャラ)のほうをむく」とは違い、対象キャラがなくても座標さえわかれば向きがわかるというメリットがあります。
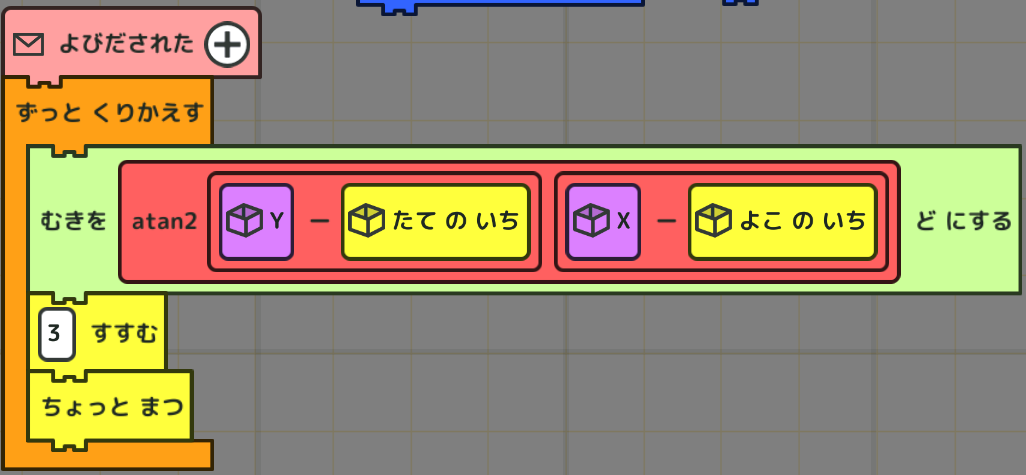
このプログラムでは、座標(X,Y)に向かって追尾します。
一番目の数値が横の位置ではなく縦の位置であることに注意!

このプログラムでは、座標(X,Y)に向かって追尾します。
一番目の数値が横の位置ではなく縦の位置であることに注意!
コメント
- わかんない(白目) - とうふ (2024-11-09 12:12:52)
- わ、わかんないッピ! -- つそこさへ (2024-11-09 18:59:39)
- cosの0と-1の位置逆になってる(下が修正後)https://d.kuku.lu/vdd62wr3s -- 名無しさん (2024-11-10 09:24:23)
- なんか雑にsin,cos使ってたらなぜか分かってきた -- とうふ (2025-01-05 21:43:32)
- 今見るとこのページめっちゃ分かりやすくまとめてくれてるのが分かる。 -- とうふ (2025-01-26 12:19:00)
- なんとか理解しなきゃな -- モア (2025-08-14 10:59:06)
