R入門
統計解析のはなし(東京図書)
最終更新:
r-intro
目次
- 目次
- T大学女子学生(1年生)200人の身長・体重・バスト・ウェスト・ヒップ・男性の身長(1986年調査)(表1.1.1)(pp.2-8)
- 女子大生200人の身長を1cmきざみで整理した度数分布表(p.10)
- 女子大生200人の身長を3cmきざみで整理した度数分布表(p.11)
- 女子大生200人の身長を5cmきざみで整理した度数分布表(p.12)
- 女子大生200人の身長の度数分布表とそのヒストグラム(pp.17-19)
- 女子大生200人の体重の度数分布表とそのヒストグラム(p.20)
- 女子大生200人のバストの度数分布表とそのヒストグラム(p.21)
- 女子大生200人の身長の標本平均(pp.23-24)
- 女子大生200人の身長の中央値(p.25)
- 女子大生200人の身長の分散と不偏分散(pp.31-32)
- 女子大生200人の身長の標準偏差と不偏分散の平方根(p.33)
- 女子大生200人による6つの変量(身長、体重、バスト、ウエスト、ヒップ、男性の身長)の平均、分散、標準偏差、最小値、最大値(p.36)
- 女子大生200人の身長の歪度(p.41)
- 女子大生200人の身長の尖度(p.42)
- 女子大生200人の体重とバストの歪度と尖度(p.43)
- 2項分布n=10,p=0.5のときの確率分布(p.84)
- 2項分布n=10,p=0.1のときの確率分布(p.85)
- 2項分布n=100,p=0.01のときの確率分布(p.86)
- λ=1のときのポアソン分布(pp.93-94)
- 1年間に馬に蹴り殺された兵士の数とポアソン分布(pp.94-95)
- 標準正規分布 N(0, 1^2) の値とグラフ(pp.103-104)
- 正規分布の各αパーセント点(p.114)
- χ^2分布の各αパーセント点(p.121)
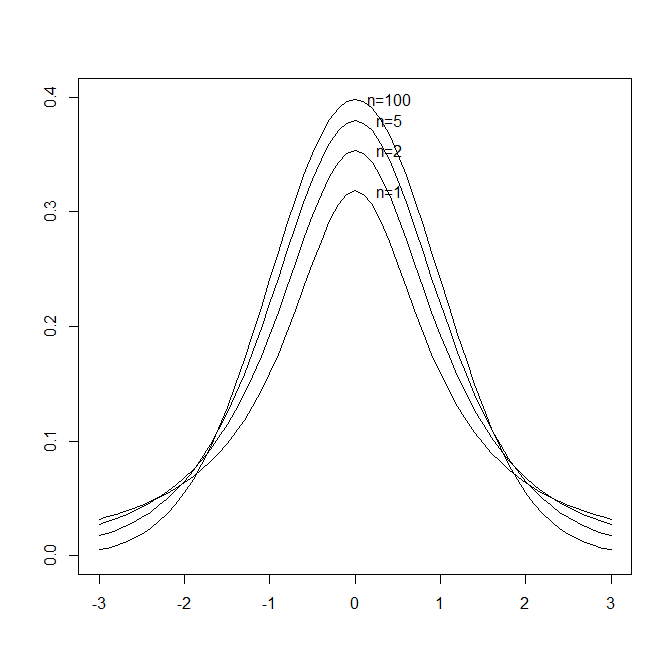
- t分布のグラフ(p.123)
- t分布の各αパーセント点(p.125)
- F分布の各αパーセント点(p.128)
- 母分散σ^2が既知の場合の、女子大生200名の身長の母平均の区間推定(pp.146-148)
- 母分散σ^2が未知の場合の、女子大生200名の身長の母平均の区間推定(pp.148-150)
- 溶液のpH値の99%信頼区間(pp.150-151)
- アオスジアゲハ夏型の体長の90%信頼区間(pp.151-152)
- 乗用車のレギュラーガソリンの平均売り上げ量の95%信頼区間(pp.152-153)
- サラダ油800g缶の平均内容量の99%信頼区間(p.153)
- T大学の女子大生の平均I.Q.の95%信頼区間(p.154)
- 新型ナットの平均内径の99%信頼区間(pp.154-155)
- 女子大生200人の身長の母分散の90%信頼区間(pp.163-164)
- 自動車の燃費の母分散の95%信頼区間(pp.165-166)
- スコップの柄の直径の2つの母分散の比の90%信頼区間(pp.167-168)
- 母比率p(バストが85cm以上の女子大生の割合)を95%信頼区間で区間推定(pp.xxx-xxx)
T大学女子学生(1年生)200人の身長・体重・バスト・ウェスト・ヒップ・男性の身長(1986年調査)(表1.1.1)(pp.2-8)
CSVファイルはこちら。
no, height, weight, bust, waist, hip, male
1, 151, 48, 81, 60, 86, 175
2, 154, 44, 75, 60, 78, 176
3, 160, 48, 80, 58, 85, 178
4, 160, 52, 86, 63, 91, 180
5, 163, 58, 90, 66, 92, 172
6, 156, 58, 80, 68, 93, 175
7, 158, 62, 83, 66, 91, 172
8, 156, 52, 85, 66, 90, 170
9, 154, 45, 80, 61, 88, 170
10, 160, 55, 80, 63, 90, 180
11, 154, 54, 85, 63, 90, 170
12, 162, 47, 80, 58, 90, 175
13, 156, 43, 80, 63, 87, 180
14, 162, 53, 78, 60, 85, 180
15, 157, 54, 83, 63, 90, 175
16, 162, 64, 94, 68, 92, 175
17, 162, 47, 80, 63, 88, 178
18, 169, 61, 80, 66, 93, 185
19, 150, 38, 75, 62, 83, 178
20, 162, 48, 83, 59, 85, 178
21, 154, 47, 77, 63, 87, 180
22, 152, 58, 85, 66, 93, 170
23, 161, 46, 80, 58, 84, 175
24, 160, 47, 78, 59, 80, 172
25, 160, 45, 80, 56, 80, 170
26, 153, 40, 80, 56, 81, 170
27, 155, 40, 80, 58, 83, 170
28, 163, 55, 80, 63, 87, 170
29, 160, 62, 84, 63, 95, 176
30, 159, 50, 85, 58, 80, 175
31, 164, 50, 81, 62, 88, 177
32, 158, 46, 78, 63, 83, 176
33, 150, 45, 85, 58, 80, 178
34, 155, 49, 82, 63, 82, 178
35, 157, 53, 82, 63, 88, 170
36, 161, 57, 85, 61, 92, 170
37, 168, 60, 80, 66, 93, 175
38, 162, 55, 80, 63, 88, 175
39, 153, 47, 80, 63, 88, 175
40, 154, 50, 80, 60, 85, 170
41, 158, 53, 79, 61, 90, 180
42, 151, 46, 82, 61, 85, 170
43, 155, 50, 82, 60, 84, 175
44, 155, 45, 80, 60, 85, 180
45, 165, 50, 80, 60, 85, 185
46, 165, 51, 82, 62, 90, 178
47, 154, 48, 82, 60, 90, 178
48, 148, 48, 78, 62, 90, 170
49, 169, 55, 82, 61, 87, 185
50, 158, 54, 87, 63, 88, 178
51, 146, 43, 82, 60, 87, 175
52, 166, 63, 93, 63, 98, 176
53, 161, 53, 82, 62, 90, 180
54, 143, 42, 80, 60, 80, 170
55, 156, 46, 80, 57, 92, 172
56, 156, 69, 98, 72, 98, 170
57, 149, 47, 75, 60, 82, 170
58, 162, 48, 76, 61, 90, 180
59, 159, 50, 80, 66, 85, 182
60, 164, 55, 80, 63, 90, 178
61, 162, 45, 78, 60, 84, 180
62, 167, 49, 80, 60, 84, 178
63, 159, 51, 83, 60, 86, 178
64, 153, 51, 82, 63, 85, 180
65, 146, 44, 83, 61, 91, 175
66, 156, 58, 95, 65, 90, 180
67, 160, 53, 84, 63, 94, 175
68, 158, 48, 85, 58, 85, 175
69, 151, 46, 83, 59, 85, 175
70, 157, 48, 78, 63, 83, 182
71, 151, 43, 79, 57, 83, 171
72, 156, 50, 82, 58, 85, 175
73, 166, 58, 86, 66, 90, 175
74, 159, 49, 80, 63, 83, 170
75, 157, 50, 79, 60, 84, 175
76, 156, 47, 80, 62, 84, 170
77, 159, 47, 80, 60, 85, 180
78, 156, 52, 82, 63, 85, 172
79, 156, 47, 80, 61, 87, 175
80, 161, 50, 80, 60, 88, 173
81, 151, 51, 82, 63, 89, 176
82, 162, 53, 80, 60, 90, 175
83, 153, 45, 76, 60, 80, 175
84, 157, 51, 80, 61, 89, 178
85, 153, 57, 90, 66, 93, 175
86, 159, 56, 85, 64, 98, 185
87, 157, 52, 82, 60, 88, 170
88, 158, 52, 85, 63, 88, 175
89, 159, 51, 83, 63, 89, 175
90, 159, 48, 80, 58, 87, 175
91, 159, 49, 83, 60, 88, 175
92, 153, 45, 78, 58, 80, 175
93, 153, 45, 80, 59, 83, 170
94, 164, 50, 80, 60, 82, 175
95, 157, 53, 80, 63, 93, 172
96, 157, 45, 78, 59, 80, 175
97, 155, 56, 86, 63, 90, 170
98, 149, 53, 86, 66, 93, 176
99, 160, 52, 82, 62, 92, 175
100, 150, 46, 80, 63, 85, 173101, 161, 48, 80, 60, 85, 178
102, 155, 51, 82, 61, 87, 175
103, 156, 48, 80, 58, 83, 178
104, 156, 50, 82, 60, 90, 173
105, 151, 43, 80, 59, 82, 173
106, 153, 50, 79, 62, 89, 170
107, 161, 54, 85, 63, 85, 180
108, 165, 58, 88, 63, 90, 180
109, 155, 49, 78, 62, 85, 172
110, 156, 50, 80, 63, 88, 180
111, 165, 58, 88, 63, 90, 181
112, 156, 48, 82, 60, 80, 178
113, 154, 48, 80, 62, 90, 173
114, 160, 55, 81, 63, 92, 173
115, 159, 59, 85, 63, 94, 180
116, 155, 56, 82, 62, 93, 165
117, 165, 63, 83, 64, 85, 175
118, 151, 45, 83, 60, 85, 173
119, 156, 48, 80, 60, 80, 180
120, 158, 44, 78, 58, 80, 180
121, 155, 48, 81, 61, 85, 172
122, 162, 51, 86, 63, 90, 175
123, 163, 48, 85, 62, 89, 180
124, 153, 51, 78, 63, 82, 175
125, 157, 44, 80, 58, 83, 175
126, 153, 50, 82, 60, 88, 175
127, 151, 40, 79, 57, 80, 178
128, 153, 48, 83, 63, 85, 178
129, 153, 47, 82, 61, 86, 175
130, 153, 48, 83, 60, 84, 180
131, 162, 52, 80, 60, 90, 170
132, 156, 50, 80, 62, 85, 175
133, 156, 49, 80, 63, 90, 170
134, 153, 50, 85, 63, 90, 178
135, 161, 52, 78, 60, 85, 180
136, 156, 51, 78, 60, 88, 180
137, 164, 52, 96, 61, 90, 177
138, 155, 45, 79, 63, 85, 170
139, 159, 48, 78, 60, 84, 175
140, 168, 70, 88, 70, 90, 183
141, 159, 47, 75, 59, 88, 175
142, 170, 56, 82, 58, 88, 180
143, 164, 67, 90, 66, 92, 180
144, 168, 56, 80, 61, 90, 180
145, 169, 60, 81, 63, 93, 185
146, 156, 40, 80, 56, 82, 180
147, 156, 50, 79, 63, 90, 175
148, 158, 43, 78, 57, 82, 163
149, 155, 54, 80, 63, 87, 175
150, 155, 50, 83, 62, 88, 175
151, 152, 50, 80, 65, 85, 175
152, 157, 47, 75, 62, 83, 170
153, 153, 45, 80, 60, 88, 170
154, 166, 52, 80, 60, 85, 178
155, 155, 46, 80, 60, 86, 175
156, 163, 58, 85, 69, 90, 175
157, 150, 47, 80, 59, 86, 175
158, 160, 53, 80, 63, 90, 180
159, 153, 47, 83, 63, 86, 175
160, 168, 54, 85, 62, 88, 175
161, 165, 56, 85, 63, 88, 182
162, 159, 53, 84, 62, 87, 180
163, 153, 47, 82, 60, 85, 173
164, 151, 47, 88, 60, 88, 173
165, 156, 48, 80, 60, 86, 175
166, 158, 50, 86, 62, 88, 175
167, 155, 48, 83, 60, 89, 180
168, 165, 50, 85, 58, 80, 180
169, 157, 52, 82, 60, 89, 172
170, 160, 54, 82, 63, 88, 180
171, 163, 45, 83, 60, 92, 175
172, 163, 53, 86, 65, 90, 173
173, 162, 48, 85, 63, 85, 185
174, 167, 57, 83, 63, 85, 178
175, 160, 53, 83, 63, 85, 180
176, 162, 43, 80, 60, 85, 175
177, 158, 50, 85, 60, 85, 175
178, 159, 43, 78, 62, 84, 175
179, 159, 56, 71, 65, 87, 181
180, 160, 47, 85, 60, 85, 180
181, 162, 51, 80, 63, 87, 175
182, 162, 54, 80, 63, 87, 180
183, 158, 53, 84, 63, 87, 172
184, 147, 45, 80, 62, 90, 173
185, 164, 60, 87, 66, 94, 178
186, 147, 38, 85, 58, 80, 173
187, 156, 43, 80, 56, 84, 173
188, 161, 60, 92, 63, 95, 178
189, 160, 46, 78, 60, 84, 180
190, 154, 53, 84, 64, 85, 170
191, 163, 54, 83, 63, 92, 180
192, 158, 45, 83, 57, 89, 165
193, 157, 54, 85, 63, 90, 170
194, 164, 63, 85, 66, 85, 178
195, 152, 41, 79, 57, 86, 175
196, 157, 50, 82, 60, 90, 170
197, 155, 50, 80, 63, 88, 180
198, 163, 56, 82, 66, 90, 180
199, 155, 51, 83, 62, 90, 177
200, 152, 42, 78, 58, 86, 176女子大生200人の身長を1cmきざみで整理した度数分布表(p.10)
> dtf <- read.csv("table1_1_1.csv", header = TRUE)
> for (i in 143:170) cat(sprintf("%d %2d\n", i, length(which(dtf$height == i))))
143 1
144 0
145 0
146 2
147 2
148 1
149 2
150 4
151 9
152 4
153 17
154 8
155 16
156 22
157 13
158 12
159 15
160 14
161 8
162 15
163 8
164 7
165 7
166 3
167 2
168 4
169 3
170 1女子大生200人の身長を3cmきざみで整理した度数分布表(p.11)
> dtf <- read.csv("table1_1_1.csv", header = TRUE)
> w <- 3
> sumn <- 0
> for (i in seq(142, 169, w)) {
+ n <- length(which(dtf$height > i & dtf$height <= i + w))
+ cat(sprintf("%d~%d %2d\n", i, i + w, n))
+ sumn <- sumn + n
+ }
142~145 1
145~148 5
148~151 15
151~154 29
154~157 51
157~160 41
160~163 31
163~166 17
166~169 9
169~172 1
> cat(sprintf("計 %d\n", sumn))
計 200女子大生200人の身長を5cmきざみで整理した度数分布表(p.12)
> dtf <- read.csv("table1_1_1.csv", header = TRUE)
> w <- 5
> sumn <- 0
> for (i in seq(140, 165, w)) {
+ n <- length(which(dtf$height > i & dtf$height <= i + w))
+ cat(sprintf("%d~%d %2d\n", i, i + w, n))
+ sumn <- sumn + n
+ }
140~145 1
145~150 11
150~155 54
155~160 76
160~165 45
165~170 13
> cat(sprintf("計 %d\n", sumn))
計 200女子大生200人の身長の度数分布表とそのヒストグラム(pp.17-19)
本書では200人分の測定値をまとめているが、pp.10-11で階級に属するのは145~148であれば不等式で145<x≦148ということと約束しており、測定値に143が1つあり、その約束どおりにすると143は143~146の階級には含まれない。本計算では、その約束に従い計算している。
> dtf <- read.csv("table1_1_1.csv", header = TRUE)
> height <- dtf$height
> w <- (170 - 143) / 9
> sumn <- length(which(height > 143 & height <= 170))
> cumn <- cumrf <- 0.0
> cat("女子大生199人の身長の度数分布表\n")
女子大生199人の身長の度数分布表
> for (i in seq(143, 170 - w, w)) {
+ n <- length(which(height > i & height <= i + w))
+ rf <- n / sumn
+ cumn <- cumn + n
+ cumrf <- cumrf + rf
+ cat(sprintf("%d~%d %2d %4.1f%% %3d %5.1f%%\n", i, i + w, n, rf * 100, cumn, cumrf * 100))
+ }
143~146 2 1.0% 2 1.0%
146~149 5 2.5% 7 3.5%
149~152 17 8.5% 24 12.1%
152~155 41 20.6% 65 32.7%
155~158 47 23.6% 112 56.3%
158~161 37 18.6% 149 74.9%
161~164 30 15.1% 179 89.9%
164~167 12 6.0% 191 96.0%
167~170 8 4.0% 199 100.0%
> cat(sprintf("計 %d\n", sumn))
計 199
> hist(dtf$height, breaks = seq(143, 173, by = 3))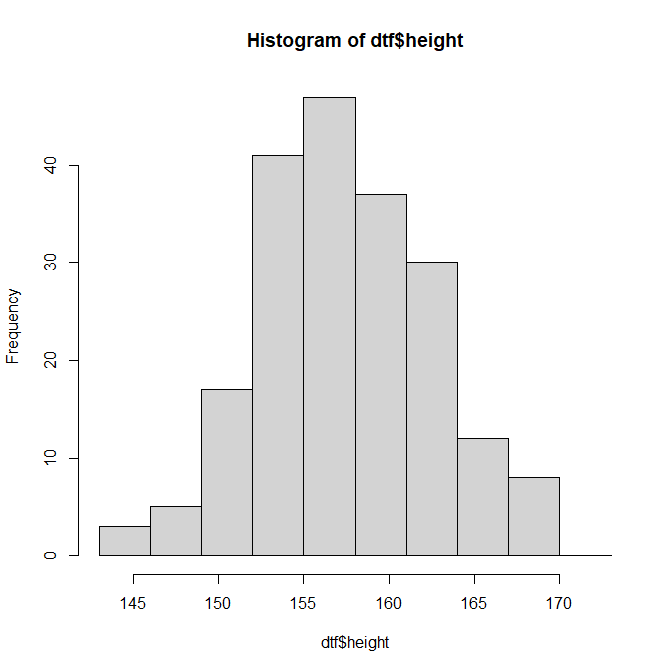
女子大生200人の体重の度数分布表とそのヒストグラム(p.20)
> dtf <- read.csv("table1_1_1.csv", header = TRUE)
> weight <- dtf$weight
> w <- (70.0 - 38) / 9
> sumn <- length(which(weight > 38 & weight <= 70.0))
> cumn <- cumrf <- 0.0
> cat("女子大生198人の体重の度数分布表\n")
女子大生198人の体重の度数分布表
> for (i in seq(38, 70 - w, w)) {
+ n <- length(which(weight > i & weight <= i + w))
+ rf <- n / sumn
+ cumn <- cumn + n
+ cumrf <- cumrf + rf
+ cat(sprintf("%.2f~%.2f %2d %4.1f%% %3d %5.1f%%\n", i, i + w, n, rf * 100, cumn, cumrf * 100))
+ }
38.00~41.56 5 2.5% 5 2.5%
41.56~45.11 29 14.6% 34 17.2%
45.11~48.67 47 23.7% 81 40.9%
48.67~52.22 53 26.8% 134 67.7%
52.22~55.78 30 15.2% 164 82.8%
55.78~59.33 20 10.1% 184 92.9%
59.33~62.89 7 3.5% 191 96.5%
62.89~66.44 4 2.0% 195 98.5%
66.44~70.00 3 1.5% 198 100.0%
> cat(sprintf("計 %d\n", sumn))
計 198
> hist(dtf$weight, breaks = seq(38, 70.0, length = 10))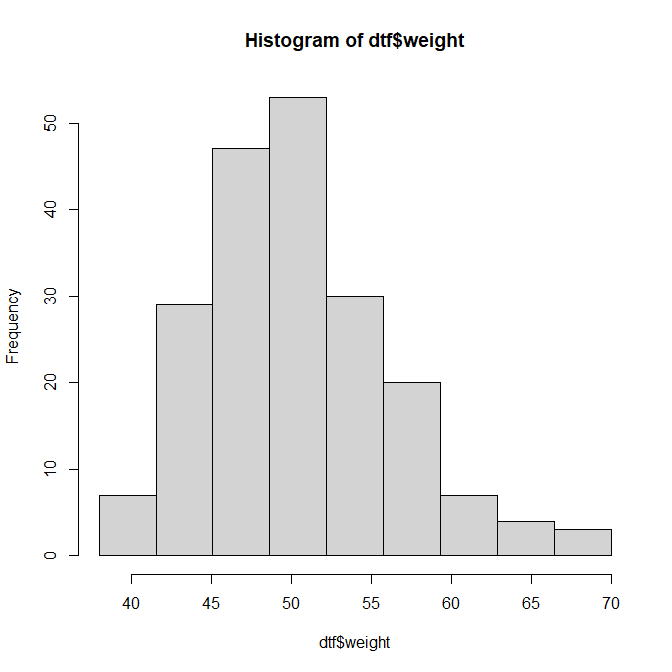
女子大生200人のバストの度数分布表とそのヒストグラム(p.21)
> dtf <- read.csv("table1_1_1.csv", header = TRUE)
> bust <- dtf$bust
> w <- 3
> sumn <- length(which(bust > 71 & bust <= 98))
> cumn <- cumrf <- 0.0
> cat("女子大生199人のバストの度数分布表\n")
女子大生199人のバストの度数分布表
> for (i in seq(71, 98 - w, w)) {
+ n <- length(which(bust > i & bust <= i + w))
+ rf <- n / sumn
+ cumn <- cumn + n
+ cumrf <- cumrf + rf
+ cat(sprintf("%d~%d %2d %4.1f%% %3d %5.1f%%\n", i, i + w, n, rf * 100, cumn, cumrf * 100))
+ }
71~74 0 0.0% 0 0.0%
74~77 8 4.0% 8 4.0%
77~80 88 44.2% 96 48.2%
80~83 53 26.6% 149 74.9%
83~86 35 17.6% 184 92.5%
86~89 6 3.0% 190 95.5%
89~92 4 2.0% 194 97.5%
92~95 3 1.5% 197 99.0%
95~98 2 1.0% 199 100.0%
> cat(sprintf("計 %d\n", sumn))
計 199
> hist(dtf$bust, breaks = seq(71, 98, length = 10))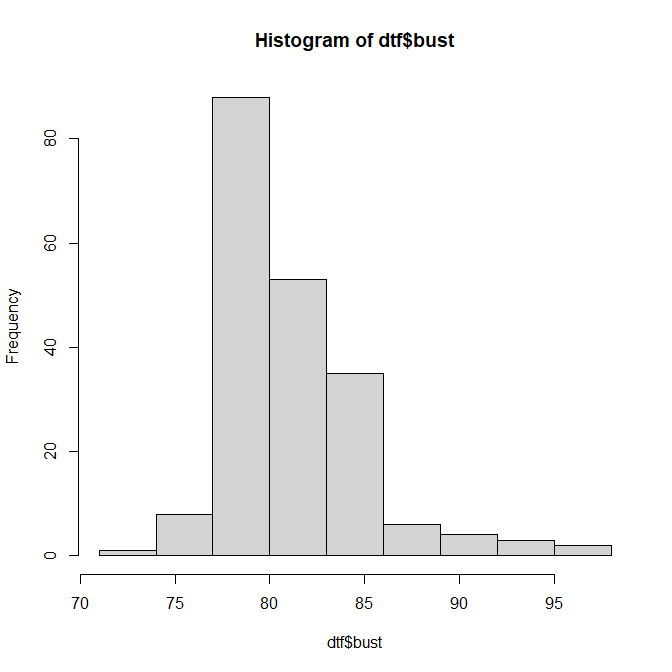
女子大生200人の身長の標本平均(pp.23-24)
> dtf <- read.csv("table1_1_1.csv", header = TRUE)
> print(mean(dtf$height))
[1] 157.775女子大生200人の身長の中央値(p.25)
> dtf <- read.csv("table1_1_1.csv", header = TRUE)
> cat(sprintf("%.2f\n", median(dtf$height)))
157.00女子大生200人の身長の分散と不偏分散(pp.31-32)
> dtf <- read.csv("table1_1_1.csv", header = TRUE)
> xi <- dtf$height
> nn <- length(xi)
> xm <- mean(xi)
> ss2 <- sum((xi - xm) ^ 2) / nn
> s2 <- sum((xi - xm) ^ 2) / (nn - 1)
> cat(sprintf("女子大生200人の身長の分散 S^2 = %.2f\n", ss2))
女子大生200人の身長の分散 S^2 = 25.42
> cat(sprintf("女子大生200人の身長の不偏分散 s^2 = %.2f\n", s2))
女子大生200人の身長の不偏分散 s^2 = 25.55女子大生200人の身長の標準偏差と不偏分散の平方根(p.33)
> dtf <- read.csv("table1_1_1.csv", header = TRUE)
> xi <- dtf$height
> nn <- length(xi)
> xm <- mean(xi)
> ss2 <- sum((xi - xm) ^ 2) / nn
> s2 <- sum((xi - xm) ^ 2) / (nn - 1)
> ss <- sqrt(ss2)
> s <- sqrt(s2)
> cat(sprintf("女子大生200人の身長の標準偏差 S = %.4f\n", ss))
女子大生200人の身長の標準偏差 S = 5.0423
> cat(sprintf("女子大生200人の身長の不偏分散の平方根 s = %.4f\n", s))
女子大生200人の身長の不偏分散の平方根 s = 5.0549女子大生200人による6つの変量(身長、体重、バスト、ウエスト、ヒップ、男性の身長)の平均、分散、標準偏差、最小値、最大値(p.36)
書籍の計算では、計算途中で適宜切り捨てを行っているらしく、分散や標準偏差はぴったり一致しない。
> dtf <- read.csv("table1_1_1.csv", header = TRUE)
> k <- 6
> nn <- nrow(dtf)
> xm <- xv <- double(k)
> xm <- apply(dtf[, -1], 2, mean)
> for (i in 1:k) xv[i] <- sum((dtf[, i + 1] - xm[i]) ^ 2 / nn)
> xs <- sqrt(xv)
> xmin <- apply(dtf[, -1], 2, min)
> xmax <- apply(dtf[, -1], 2, max)
> rdtf <- data.frame(xm, xv, xs, xmin, xmax)
> print(rdtf)
xm xv xs xmin xmax
height 157.775 25.42437 5.042259 143 170
weight 50.475 31.09937 5.576681 38 70
bust 81.870 14.02310 3.744743 71 98
waist 61.570 7.08510 2.661785 56 72
hip 87.135 15.00677 3.873858 78 98
male 175.695 16.24198 4.030133 163 185女子大生200人の身長の歪度(p.41)
> dtf <- read.csv("table1_1_1.csv", header = TRUE)
> xi <- dtf$height
> nn <- length(xi)
> xm <- mean(xi)
> ss <- sqrt((nn - 1) / nn * var(xi))
> a3 <- sum((xi - xm) ^ 3) / (nn * ss ^ 3)
> cat(sprintf("歪度 a3 = %f\n", a3))
歪度 a3 = 0.045148女子大生200人の身長の尖度(p.42)
> dtf <- read.csv("table1_1_10.csv", header = TRUE)
> mi <- dtf$midpoint
> fi <- dtf$frequency
> nn <- sum(fi)
> xm <- sum(mi * fi) / nn
> ss2 <- sum((mi - xm) ^ 2 * fi) / nn
> ss <- sqrt(ss2)
> a4 <- sum((mi - xm) ^ 4 * fi) / (nn * ss ^ 4)
> cat(sprintf("尖度 a4 = %f\n", a4))
尖度 a4 = 2.783519女子大生200人の体重とバストの歪度と尖度(p.43)
> dtf <- read.csv("table1_1_1.csv", header = TRUE)
> rdtf <- data.frame(c(0., 0.), c(0., 0.))
> colnames(rdtf) <- c("体重", "バスト")
> rownames(rdtf) <- c("歪度 a3", "尖度 a4")
> for (i in 3:4) {
+ xi <- dtf[, i]
+ nn <- length(xi)
+ xm <- mean(xi)
+ ss <- sqrt((nn - 1) / nn * var(xi))
+ a3 <- sum((xi - xm) ^ 3) / (nn * ss ^ 3)
+ a4 <- sum((xi - xm) ^ 4) / (nn * ss ^ 4) - 3
+ rdtf[1, i - 2] <- a3
+ rdtf[2, i - 2] <- a4
+ }
> print(rdtf)
体重 バスト
歪度 a3 0.6519655 1.190016
尖度 a4 0.8305713 3.1709112項分布n=10,p=0.5のときの確率分布(p.84)
> n <- 10
> p <- 0.5
> xx <- 0:10
> pp <- dbinom(xx, n, p)
> print(data.frame(xx, pp))
xx pp
1 0 0.0009765625
2 1 0.0097656250
3 2 0.0439453125
4 3 0.1171875000
5 4 0.2050781250
6 5 0.2460937500
7 6 0.2050781250
8 7 0.1171875000
9 8 0.0439453125
10 9 0.0097656250
11 10 0.00097656252項分布n=10,p=0.1のときの確率分布(p.85)
> n <- 10
> p <- 0.1
> xx <- 0:6
> pp <- dbinom(xx, n, p)
> print(data.frame(xx, pp))
xx pp
1 0 0.348678440
2 1 0.387420489
3 2 0.193710244
4 3 0.057395628
5 4 0.011160261
6 5 0.001488035
7 6 0.0001377812項分布n=100,p=0.01のときの確率分布(p.86)
> n <- 100
> p <- 0.01
> xx <- 0:6
> pp <- dbinom(xx, n, p)
> print(data.frame(xx, pp))
xx pp
1 0 0.3660323413
2 1 0.3697296376
3 2 0.1848648188
4 3 0.0609991658
5 4 0.0149417149
6 5 0.0028977871
7 6 0.0004634508λ=1のときのポアソン分布(pp.93-94)
> # 確率変数 X=x
> x <- 0:6
> # λ = 1
> lam <- 1
> # λ = 1 のときのポアソン分布
> pp <- lam ^ x / factorial(x) * exp(-lam)
> # 計算結果の表示
> print(data.frame(X = x, P = pp))
X P
1 0 0.3678794412
2 1 0.3678794412
3 2 0.1839397206
4 3 0.0613132402
5 4 0.0153283100
6 5 0.0030656620
7 6 0.00051094371年間に馬に蹴り殺された兵士の数とポアソン分布(pp.94-95)
> # データの読み込み
> dtf <- read.csv("data/table2_2_7.csv", header = TRUE)
> # 死亡した兵士数 x
> x <- dtf$x
> # 1年間に兵士がx人死亡した軍団の数 n
> n <- dtf$n
> # 度数の合計 200
> nn <- sum(n)
> # 相対度数 x/200
> rf <- n / nn
> # 死亡した兵士数の平均 x~
> xm <- sum(x * rf)
> # ポアソン分のパラメーターλは平均を採用
> lam <- xm
> # 階級ごとの確率 P(X=x)
> pp <- lam ^ x / factorial(x) * exp(-lam)
> # 計算結果の表示
> print(data.frame(x, n, 相対度数 = rf, ポアソン分布 = pp))
x n 相対度数 ポアソン分布
1 0 109 0.545 0.5433508691
2 1 65 0.325 0.3314440301
3 2 22 0.110 0.1010904292
4 3 3 0.015 0.0205550539
5 4 1 0.005 0.0031346457
6 5 0 0.000 0.0003824268標準正規分布 N(0, 1^2) の値とグラフ(pp.103-104)
> x <- seq(-4.0, 4.0, 0.5)
> y <- dnorm(x, mean = 0.0, sd = sqrt(1))
> for (i in 1:length(x)) cat(sprintf("%4.1f %8.6f\n", x[i], y[i]))
-4.0 0.000134
-3.5 0.000873
-3.0 0.004432
-2.5 0.017528
-2.0 0.053991
-1.5 0.129518
-1.0 0.241971
-0.5 0.352065
0.0 0.398942
0.5 0.352065
1.0 0.241971
1.5 0.129518
2.0 0.053991
2.5 0.017528
3.0 0.004432
3.5 0.000873
4.0 0.000134
> plot(x, y, type = "l")
> points(x, y, pch = 20, col = "black")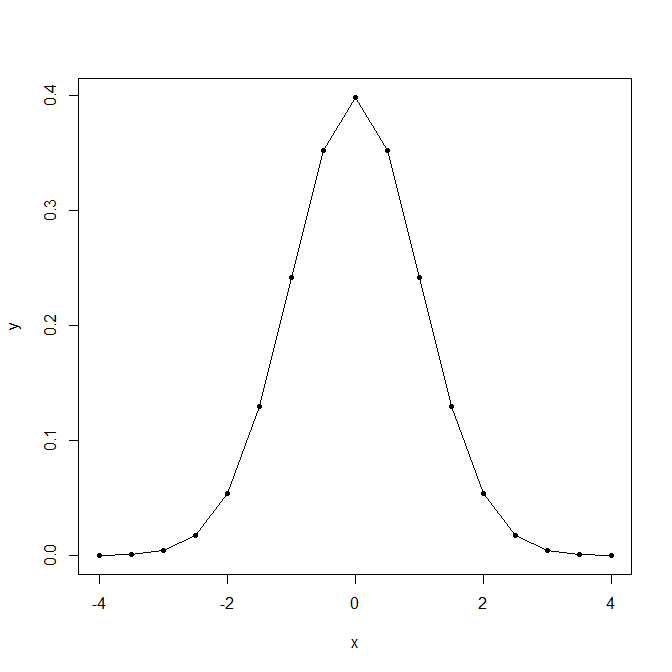
正規分布の各αパーセント点(p.114)
> m <- 0
> s <- 1
> a <- c(0.01, 0.05, 0.1)
> cat("両側パーセント点\n")
両側パーセント点
> for (i in 1:length(a)) {
+ cat(sprintf("a = %.2f, z(a/2) = %.2f\n", a[i], qnorm(p = a[i] / 2, mean = m, sd = s, lower.tail = FALSE)))
+ }
a = 0.01, z(a/2) = 2.58
a = 0.05, z(a/2) = 1.96
a = 0.10, z(a/2) = 1.64
> cat("上側パーセント点\n")
上側パーセント点
> for (i in 1:length(a)) {
+ cat(sprintf("a = %.2f, z(a) = %.2f\n", a[i], qnorm(p = a[i], mean = m, sd = s, lower.tail = FALSE)))
+ }
a = 0.01, z(a) = 2.33
a = 0.05, z(a) = 1.64
a = 0.10, z(a) = 1.28χ^2分布の各αパーセント点(p.121)
> n <- c(5, 6)
> a <- 0.05
> for (i in 1:length(n)) {
+ cat(sprintf("n = %d, a = %.2f\n", n[i], a))
+ cat("両側かつ下側 ")
+ cat(sprintf("χ_%d^2 = %.6f\n", n[i], qchisq(a / 2, n[i], lower.tail = TRUE)))
+ cat("両側かつ上側 ")
+ cat(sprintf("χ_%d^2 = %.6f\n", n[i], qchisq(a / 2, n[i], lower.tail = FALSE)))
+ cat("片側かつ下側 ")
+ cat(sprintf("χ_%d^2 = %.6f\n", n[i], qchisq(a, n[i], lower.tail = TRUE)))
+ cat("片側かつ上側 ")
+ cat(sprintf("χ_%d^2 = %.6f\n", n[i], qchisq(a, n[i], lower.tail = FALSE)))
+ }
n = 5, a = 0.05
両側かつ下側 χ_5^2 = 0.831212
両側かつ上側 χ_5^2 = 12.832502
片側かつ下側 χ_5^2 = 1.145476
片側かつ上側 χ_5^2 = 11.070498
n = 6, a = 0.05
両側かつ下側 χ_6^2 = 1.237344
両側かつ上側 χ_6^2 = 14.449375
片側かつ下側 χ_6^2 = 1.635383
片側かつ上側 χ_6^2 = 12.591587t分布のグラフ(p.123)
> x <- seq(-3, 3, 0.1)
> plot(0, 0, xlim = c(-3, 3), ylim = c(0, 0.4), xlab = "", ylab = "", type = "n")
> for (i in c(1, 2, 5, 100)) {
+ lines(x, dt(x, i))
+ text(0.4, dt(0, i), sprintf("n=%d", i))
+ }
t分布の各αパーセント点(p.125)
> n <- c(5, 10)
> a <- c(0.05, 0.01)
> for (i in 1:length(n)) {
+ for (j in 1:length(a)) {
+ cat(sprintf("両側 a = %.2f t_%d(a/2) = %.3f\n", a[j], n[i], qt(a[j] / 2, n[i], lower.tail = FALSE)))
+ cat(sprintf("片側 a = %.2f t_%d(a) = %.3f\n", a[j], n[i], qt(a[j], n[i], lower.tail = FALSE)))
+ }
+ }
両側 a = 0.05 t_5(a/2) = 2.571
片側 a = 0.05 t_5(a) = 2.015
両側 a = 0.01 t_5(a/2) = 4.032
片側 a = 0.01 t_5(a) = 3.365
両側 a = 0.05 t_10(a/2) = 2.228
片側 a = 0.05 t_10(a) = 1.812
両側 a = 0.01 t_10(a/2) = 3.169
片側 a = 0.01 t_10(a) = 2.764F分布の各αパーセント点(p.128)
自由度(4,6)の95パーセント点と99パーセント点を求める。
> qf(0.05, 4, 6, lower.tail = FALSE)
[1] 4.533677
> qf(0.01, 4, 6, lower.tail = FALSE)
[1] 9.148301母分散σ^2が既知の場合の、女子大生200名の身長の母平均の区間推定(pp.146-148)
> d <- c(159, 158, 151, 167, 151)
> d <- c(d, 160, 160, 158, 160, 158)
> s <- 5.04
> xm <- mean(d)
> ah <- 0.05
> z <- qnorm(ah / 2, lower.tail = FALSE)
> nn <- length(d)
> print(xm)
[1] 158.2
> print(z)
[1] 1.959964
> print(s)
[1] 5.04
> print(nn)
[1] 10
> a <- xm - z * s / sqrt(nn)
> b <- xm + z * s / sqrt(nn)
> # 母平均μの95%信頼区間
> cat(sprintf("%.1f≦μ≦%.1f\n", a, b))
155.1≦μ≦161.3
> ah <- 0.01
> z <- qnorm(ah / 2, lower.tail = FALSE)
> a <- xm - z * s / sqrt(nn)
> b <- xm + z * s / sqrt(nn)
> # 母平均μの99%信頼区間
> cat(sprintf("%.1f≦μ≦%.1f\n", a, b))
154.1≦μ≦162.3母分散σ^2が未知の場合の、女子大生200名の身長の母平均の区間推定(pp.148-150)
> d1 <- c(159, 158, 151, 167, 151)
> d1 <- c(d1, 160, 160, 158, 160, 158)
> xm <- mean(d1)
> s <- sd(d1)
> ah <- 0.05
> nn <- length(d1)
> t9 <- qt(ah / 2, nn - 1, lower.tail = FALSE)
> print(xm)
[1] 158.2
> print(t9)
[1] 2.262157
> print(s)
[1] 4.613988
> print(nn)
[1] 10
> a <- xm - t9 * s / sqrt(nn)
> b <- xm + t9 * s / sqrt(nn)
> # 母平均μの95%信頼区間
> cat(sprintf("%.1f≦μ≦%.1f\n", a, b))
154.9≦μ≦161.5
> d2 <- c(156, 160, 153, 153, 166)
> d2 <- c(d2, 157, 158, 169, 165, 159)
> xm <- mean(d2)
> s <- sd(d2)
> ah <- 0.05
> nn <- length(d2)
> t9 <- qt(ah / 2, nn - 1, lower.tail = FALSE)
> a <- xm - t9 * s / sqrt(nn)
> b <- xm + t9 * s / sqrt(nn)
> # 母平均μの95%信頼区間
> cat(sprintf("%.1f≦μ≦%.1f\n", a, b))
155.7≦μ≦163.5
> xm <- mean(c(d1, d2))
> s <- sd(c(d1, d2))
> ah <- 0.05
> nn <- length(c(d1, d2))
> t19 <- qt(ah / 2, nn - 1, lower.tail = FALSE)
> a <- xm - t19 * s / sqrt(nn)
> b <- xm + t19 * s / sqrt(nn)
> # 母平均μの95%信頼区間
> cat(sprintf("%.1f≦μ≦%.1f\n", a, b))
156.6≦μ≦161.2溶液のpH値の99%信頼区間(pp.150-151)
> x <- c(7.86, 7.89, 7.84, 7.90, 7.82)
> nn <- length(x)
> xm <- mean(x)
> s <- sd(x)
> degf <- nn - 1
> ah <- 0.01
> tval <- qt(ah / 2, degf, lower.tail = FALSE)
> a <- xm - tval * s / sqrt(nn)
> b <- xm + tval * s / sqrt(nn)
> # 溶液のpHの99%信頼区間
> cat(sprintf("%.3f≦μ≦%.3f\n", a, b))
7.793≦μ≦7.931アオスジアゲハ夏型の体長の90%信頼区間(pp.151-152)
> x <- c(76, 85, 82, 83, 76, 78)
> nn <- length(x)
> xm <- mean(x)
> s <- sd(x)
> degf <- nn - 1
> ah <- 0.1
> tval <- qt(ah / 2, degf, lower.tail = FALSE)
> a <- xm - tval * s / sqrt(nn)
> b <- xm + tval * s / sqrt(nn)
> # アオスジアゲハ夏型の体長の90%信頼区間
> cat(sprintf("%.3f≦μ≦%.3f\n", a, b))
76.835≦μ≦83.165乗用車のレギュラーガソリンの平均売り上げ量の95%信頼区間(pp.152-153)
> x <- c(45, 39, 42, 57, 28, 33, 40, 51)
> nn <- length(x)
> degf <- nn - 1
> ah <- 0.05
> xm <- mean(x)
> s <- sd(x)
> tval <- qt(ah / 2, degf, lower.tail = FALSE)
> a <- xm - tval * s / sqrt(nn)
> b <- xm + tval * s / sqrt(nn)
> # 乗用車のレギュラーガソリンの平均売り上げ量の95%信頼区間
> cat(sprintf("%.1f≦μ≦%.1f\n", a, b))
34.1≦μ≦49.6サラダ油800g缶の平均内容量の99%信頼区間(p.153)
> x <- c(807, 811, 801, 798, 798, 795, 803, 805, 804)
> nn <- length(x)
> degf <- nn - 1
> ah <- 0.01
> xm <- mean(x)
> s <- sd(x)
> tval <- qt(ah / 2, degf, lower.tail = FALSE)
> a <- xm - tval * s / sqrt(nn)
> b <- xm + tval * s / sqrt(nn)
> # サラダ油800g缶の平均内容量の99%信頼区間
> cat(sprintf("%.1f≦μ≦%.1f\n", a, b))
796.8≦μ≦808.0T大学の女子大生の平均I.Q.の95%信頼区間(p.154)
> nn <- 500
> ah <- 0.05
> xm <- 112
> s <- 9.5
> z <- qnorm(ah / 2, mean = 0, sd = 1, lower.tail = FALSE)
> a <- xm - z * s / sqrt(nn)
> b <- xm + z * s / sqrt(nn)
> # T大学の女子大生の平均I.Q.の95%信頼区間
> cat(sprintf("%.1f≦μ≦%.1f\n", a, b))
111.2≦μ≦112.8新型ナットの平均内径の99%信頼区間(pp.154-155)
> x <- c(1.29, 1.34, 1.31, 1.30, 1.30)
> nn <- length(x)
> degf <- nn - 1
> xm <- mean(x)
> s <- 0.015
> ah <- 0.01
> z <- qnorm(ah / 2, mean = 0, sd = 1, lower.tail = FALSE)
> a <- xm - z * s / sqrt(nn)
> b <- xm + z * s / sqrt(nn)
> # 新型ナットの平均内径の99%信頼区間
> cat(sprintf("%.3f≦μ≦%.3f\n", a, b))
1.291≦μ≦1.325女子大生200人の身長の母分散の90%信頼区間(pp.163-164)
> x <- c(159, 158, 151, 167, 151)
> x <- c(x, 160, 160, 158, 160, 158)
> xm <- mean(x)
> nn <- length(x)
> s2 <- var(x)
> degf <- nn - 1
> ah <- 0.1
> ca <- qchisq(1 - ah / 2, degf, lower.tail = FALSE)
> cb <- qchisq(ah / 2, degf, lower.tail = FALSE)
> a <- (nn - 1) * s2 / cb
> b <- (nn - 1) * s2 / ca
> # 女子大生200人の身長の母分散の90%信頼区間
> cat(sprintf("%.2f≦σ^2≦%.2f\n", a, b))
11.32≦σ^2≦57.62自動車の燃費の母分散の95%信頼区間(pp.165-166)
> x <- c(15.4, 16.1, 15.7, 16.6, 14.9, 15.5, 16.2)
> nn <- length(x)
> xm <- mean(x)
> s2 <- var(x)
> degf <- nn - 1
> ah <- 0.05
> ca <- qchisq(1 - ah / 2, degf, lower.tail = FALSE)
> cb <- qchisq(ah / 2, degf, lower.tail = FALSE)
> a <- (nn - 1) * s2 / cb
> b <- (nn - 1) * s2 / ca
> # 自動車の燃費の母分散の95%信頼区間
> cat(sprintf("%.2f≦σ^2≦%.2f\n", a, b))
0.14≦σ^2≦1.58スコップの柄の直径の2つの母分散の比の90%信頼区間(pp.167-168)
> x1 <- c(5.47, 5.62, 5.52, 5.77, 5.53, 5.39)
> x2 <- c(5.63, 5.46, 5.53, 5.54, 5.59)
> x1m <- mean(x1)
> x2m <- mean(x2)
> s12 <- var(x1)
> s22 <- var(x2)
> nn1 <- length(x1)
> nn2 <- length(x2)
> degf1 <- nn1 - 1
> degf2 <- nn2 - 1
> ah <- 0.1
> ff1 <- qf(1 - ah / 2, degf1, degf2, lower.tail = FALSE)
> ff2 <- qf(ah / 2, degf1, degf2, lower.tail = FALSE)
> a <- s12 / s22 / ff2
> b <- s12 / s22 / ff1
> # スコップの柄の直径の2つの母分散の比の90%信頼区間
> cat(sprintf("%.2f≦σ1^2/σ2^2≦%.2f\n", a, b))
0.67≦σ1^2/σ2^2≦21.67母比率p(バストが85cm以上の女子大生の割合)を95%信頼区間で区間推定(pp.xxx-xxx)
> x <- c(80, 83, 83, 83, 81, 78, 83, 83, 80, 85)
> x <- c(x, 82, 80, 90, 85, 80, 82, 87, 81, 83, 85)
> nn <- length(x)
> ah <- 0.05
> m <- 5
> z <- qnorm(ah / 2, lower.tail = FALSE)
> a <- m / nn - z * sqrt(m / nn * (1 - m / nn) / nn)
> b <- m / nn + z * sqrt(m / nn * (1 - m / nn) / nn)
> # N=20におけるバスト85cm以上の女子大生の母比率pの95%信頼区間
> # (標本数Nが大きい場合の公式による)
> cat(sprintf("%.2f≦p≦%.2f\n", a, b))
0.06≦p≦0.44
> d1 <- 2 * (nn - m + 1)
> d2 <- 2 * m
> e1 <- 2 * (m + 1)
> e2 <- 2 * (nn - m)
> fd <- qf(ah / 2, d1, d2, lower.tail = FALSE)
> fe <- qf(ah / 2, e1, e2, lower.tail = FALSE)
> a <- d2 / (d1 * fd + d2)
> b <- e1 * fe / (e1 * fe + e2)
> # N=20におけるバスト85cm以上の女子大生の母比率pの95%信頼区間
> # (標本数Nが小さい場合の公式による)
> cat(sprintf("%.2f≦p≦%.2f\n", a, b))
0.09≦p≦0.49
> nn <- 200
> m <- 45
> a <- m / nn - z * sqrt(m / nn * (1 - m / nn) / nn)
> b <- m / nn + z * sqrt(m / nn * (1 - m / nn) / nn)
> # N=200におけるバスト85cm以上の女子大生の母比率pの95%信頼区間
> cat(sprintf("%.3f≦p≦%.3f\n", a, b))
0.167≦p≦0.283