R入門
統計学
最終更新:
r-intro
目次
基本
平均を求める
mean関数を使う。
> x <- c(1, 2, 3, 4, 5, 6, 7)
> mean(x)
[1] 4範囲を求める
統計学における「範囲」とは、データのとる値の最大値から最小値を引いた差のこと。Rにはこれを直接求める関数は標準で搭載されていないが、それに近い動作をする関数はある。
range関数は、引数に与えたベクトルの最小値と最大値をベクトルで返す。これを利用して範囲を求めることができる。ただしmax関数とmin関数を組み合わせた計算と手順に大差はない。
> d <- c(161, 165, 160, 164, 165, 163, 164, 162, 164, 170)
> range(d)
[1] 160 170
> print(range(d)[2] - range(d)[1]) # 範囲
[1] 10
> print(max(d) - min(d)) # 範囲
[1] 10χ 2 分布におけるパーセント点
> # 自由度5のχ^2分布における、下側5パーセント点
> qchisq(0.05, 5)
[1] 1.145476
> # 自由度5のχ^2分布における、上側5パーセント点
> qchisq(0.05, 5, lower.tail = FALSE)
[1] 11.0705
> qchisq(1 - 0.05, 5)
[1] 11.0705χ^2分布におけるp値
> # 自由度5のχ^2分布における、確率変数が12のときの下側p値
> pchisq(12, 5)
[1] 0.9652122
> # 自由度5のχ^2分布における、確率変数が12のときの上側p値
> pchisq(12, 5, lower.tail = FALSE)
[1] 0.03478778正規分布
正規分布の確率密度関数の値を得る
dnorm関数を使う。よく見かける平均0、標準偏差が1の正規分布に従う、確率密度関数のグラフは以下のとおり。
> x <- seq(-5, 5, 0.1)
> y <- dnorm(x, mean = 0, sd = 1)
> plot(x, y, type = "l")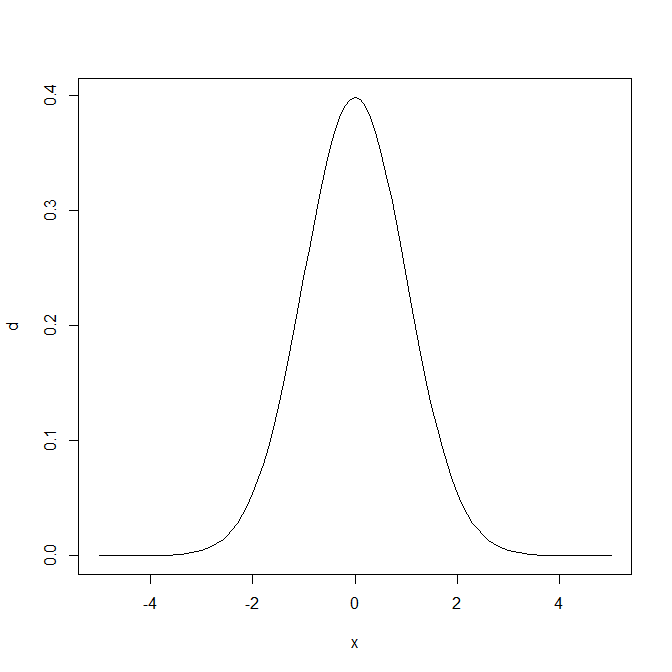
この正規分布で確率変数(横軸)が0のときの確率密度関数の値(縦軸の値)は、図より0.4程度と推察されるが、それをより正確に求めるにはdnorm関数で次のようにする。
> dnorm(0.0, mean = 0, sd = 1)
[1] 0.3989423dnorm関数は、meanオプションを省略すると0、sdオプションを省略すると1が指定されたものとして計算をする。よって、この例では次のようにしても同じ。
> dnorm(0.0)
[1] 0.3989423正規分布の分布関数の値を得る
pnorm関数を使う。平均が0、標準偏差が1の正規分布における-1における分布関数は以下のとおり。
> pnorm(-1, mean = 0, sd = 1)
[1] 0.1586553この0.1586553…という値は、以下の確率密度関数のグラフにおける、緑色で塗った箇所の面積である。
> x <- seq(-5, 5, 0.1)
> y <- dnorm(x, mean = 0, sd = 1)
> xp <- seq(-5, -1, 0.1)
> yp <- dnorm(xp, mean = 0, sd = 1)
> plot(x, y, type = "l")
> polygon(c(xp, -1), c(yp, 0), col = "green")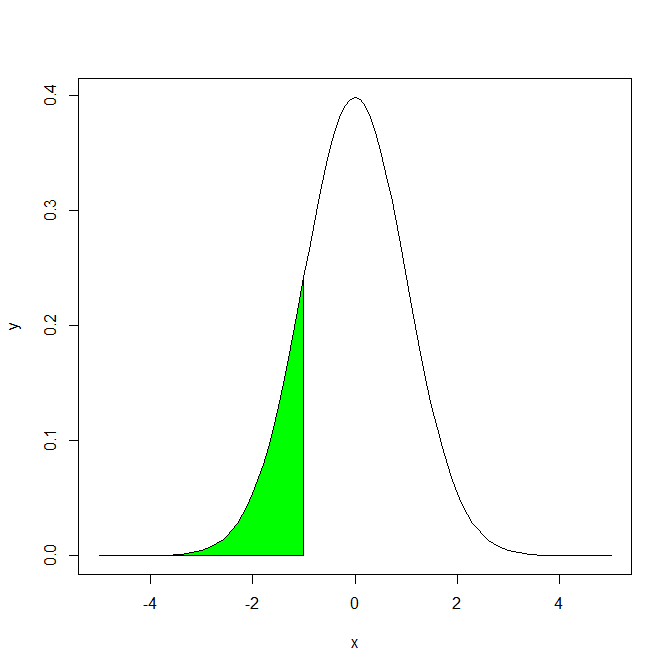
この関数を使うと、いわゆる1σ(いちしぐま)の範囲(平均値±標準偏差)の値が出る確率を簡単に求めることができる。分布関数とは、確率変数が指定の値より小さい値をとるときの確率であるため、σ(上記の例では1)における分布関数の値から、-σ(上記の例では-1)における分布関数の値を引けばよい。
> pnorm(1, mean = 0, sd = 1) - pnorm(-1, mean = 0, sd = 1)
[1] 0.6826895標準正規分布(平均0、標準偏差1)において、平均値±標準偏差の範囲になる確率は0.6826895…(約68%)である。
正規分布における分布関数の下側、上側、両側の値を求める
pnorm関数を使う。以下は、平均10、分散3^2(標準偏差3)の正規分布において、確率変数が15の場合の下側、上側、両側を求めた例。なお、値は下側0.9522、上側0.04779、両側0.09558。
> pnorm(15, mean = 10, sd = 3)
[1] 0.9522096
> pnorm(15, mean = 10, sd = 3, lower.tail = FALSE)
[1] 0.04779035
> 1 - pnorm(15, mean = 10, sd = 3)
[1] 0.04779035
> pnorm(15, mean = 10, sd = 3, lower.tail = FALSE) * 2
[1] 0.0955807
> (1 - pnorm(15, mean = 10, sd = 3)) * 2
[1] 0.0955807特に何も指定しなければ分布関数の定義のとおりに下側を返す。上側を得るにはlower.tailオプションをFALSEとするか、全体を1から引く。両側は上側を2倍する。
正規分布における-σからσ(-2σから2σ)の確率(面積)を求める
pnorm関数を使う。正規分布における累積分布関数(-∞から指定の確率変数までの定積分)はpnorm関数で得られ、それを使うことで確率(面積)を求めることができる。
正規分布はσは68%、2σは95%とよく言われるが、それを求めてみる。
平均0、標準偏差が1の正規分布について、-∞から-1まで、-∞から1までそれぞれ定積分(確率(面積))を求める。
> pnorm(-1)
[1] 0.1586553
> pnorm(1)
[1] 0.8413447いわゆるσ=1というのは、確率変数が-1から1までの範囲の定積分(面積)であるから、後者から前者を引けばよい。
> pnorm(1) - pnorm(-1)
[1] 0.68268952σが95%も同様に求まる。
> pnorm(2) - pnorm(-2)
[1] 0.9544997正規分布における下側パーセント点、上側パーセント点、両側パーセント点を求める。
qnorm関数を使う。以下は、平均10、分散3^2(標準偏差3)の正規分布における、下側5パーセント点、上側5パーセント点、両側5パーセント点を求めた例。それぞれ下側5.065、上側14.93、両側15.88である。
> qnorm(0.05, mean = 10, sd = 3)
[1] 5.065439
> qnorm(0.05, mean = 10, sd = 3, lower.tail = FALSE)
[1] 14.93456
> qnorm(1 - 0.05, mean = 10, sd = 3)
[1] 14.93456
> qnorm(0.05 / 2, mean = 10, sd = 3, lower.tail = FALSE)
[1] 15.87989
> qnorm(1 - 0.05 / 2, mean = 10, sd = 3)
[1] 15.879895%であれば、0.05と指定する。
何も指定しなければ、下側パーセント点の値を返す。
上側パーセント点はlower.tailオプションをFALSEとするか「1 - 0.05」とする。
両側パーセント点は「0.05 / 2」や「1 - 0.05 / 2」のように2で割るのがポイント。
確率変数 X が正規分布 N(μ, σ^2) に従うときの確率 P を求める
確率変数 X が正規分布 N(13, 4^2) に従うときの、次の確率 P それぞれ求める。
(1) P (7≦X≦19), (2) P (1≦X≦25), (3) P (X≦20)なお、答えはそれぞれ 0.8663…, 0.9973…, 0.9599… である。
> # (1)
> pnorm(19, 13, 4) - pnorm(7, 13, 4)
[1] 0.8663856
> # (2)
> pnorm(25, 13, 4) - pnorm(1, 13, 4)
[1] 0.9973002
> # (3)
> pnorm(20, 13, 4)
[1] 0.9599408正規分布におけるパーセント点を求める
> # 平均10、分散3^2(標準偏差3)の正規分布における下側5パーセント点
> qnorm(0.05, 10, 3)
[1] 5.065439
> # 平均10、分散3^2(標準偏差3)の正規分布における上側5パーセント点
> qnorm(0.05, 10, 3, lower.tail = FALSE)
[1] 14.93456
> # 平均10、分散3^2(標準偏差3)の正規分布における両側5パーセント点
> qnorm(0.05 / 2, 10, 3, lower.tail = FALSE)
[1] 15.87989正規分布におけるp値を求める
> # 平均10、分散3^2(標準偏差3)の正規分布における確率変数が15のときの下側p値
> pnorm(15, 10, 3)
[1] 0.9522096
> # 平均10、分散3^2(標準偏差3)の正規分布における確率変数が15のときの上側p値
> pnorm(15, 10, 3, lower.tail = FALSE)
[1] 0.04779035
> # 平均10、分散3^2(標準偏差3)の正規分布における確率変数が15のときの両側p値
> pnorm(15, 10, 3, lower.tail = FALSE) * 2
[1] 0.0955807t分布
t分布における確率密度関数の値を求める
dt関数を使う。以下は確率変数が-5~5の範囲において、自由度1と5のt分布における確率密度関数の値を求めてグラフにした例。
> xx <- seq(-5, 5, 0.1)
> plot(xx, dt(xx, 5), type = "l", col = "blue")
> lines(xx, dt(xx, 1), col = "black")
> text(1.5, 0.3, "n=5", col = "blue")
> text(2, 0.2, "n=1")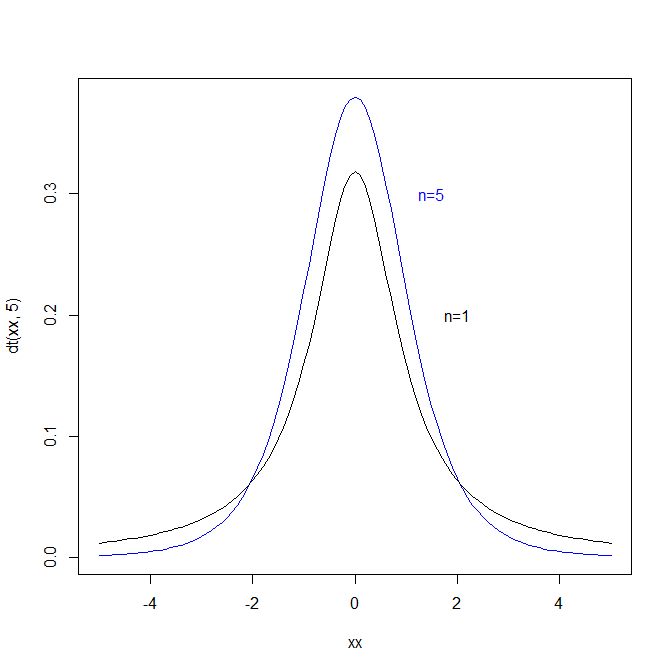
t分布における分布関数の値を求める
pt関数を使う。以下は自由度5のt分布において、確率変数Xが2における上側(=0.05096974…)、両側(=0.1019395…)の分布関数の値を求めた例。
> pt(2, 5, lower.tail = FALSE)
[1] 0.05096974
> 2 * pt(2, 5, lower.tail = FALSE)
[1] 0.1019395t分布におけるパーセント点を求める
qt関数を使う。以下は自由度5のt分布において、上側5%点(=2.015048…)、両側5%点(=2.570582…)を求めた例。
> qt(1 - 0.05, 5)
[1] 2.015048
> qt(1 - 0.05 / 2, 5)
[1] 2.570582t分布におけるパーセント点を求める
> # 自由度5のt分布における上側5パーセント点
> qt(1 - 0.05, 5)
[1] 2.015048
> # 自由度5のt分布における両側5パーセント点
> qt(1 - 0.05 / 2, 5)
[1] 2.570582t分布におけるp値を求める
> # 自由度5のt分布における、確率変数が2のときの上側p値
> pt(2, 5, lower.tail = FALSE)
[1] 0.05096974
> # 自由度5のt分布における、確率変数が2のときの両側p値
> pt(2, 5, lower.tail = FALSE) * 2
[1] 0.1019395pt関数はデフォルトでは下側p値を返す。上側p値を得たい場合はlower.tailをFALSEにする。両側p値は上側p値を2倍する。
F分布
F分布における分布関数を求める
pf関数を使う。分子の自由度が5、分母の自由度が8のときに、確率変数Xが0.21の場合の下側(=0.05117798…)、確率変数Xが3.7の場合の上側(=0.04991671…)の分布関数を求める。下側を求めるときはlower.tailオプションをTRUE、上側を求めるときはlower.tailオプションをFALSEにする。
> pf(0.21, 5, 8, lower.tail = TRUE)
[1] 0.05117798
> pf(3.69, 5, 8, lower.tail = FALSE)
[1] 0.04991671この0.05117798…と0.04991671…は、それぞれF分布を図示した図でいうところの、下側は黄緑色の面積。上側は青色の面積である。
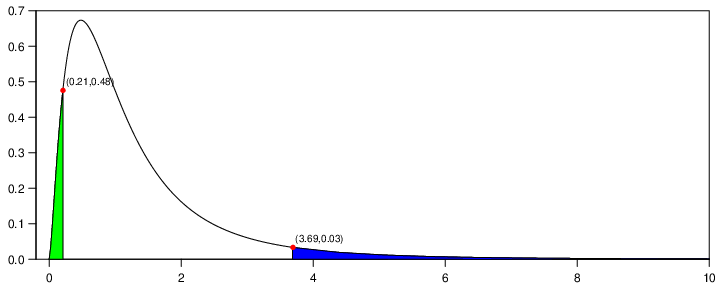
F分布におけるパーセント点を求める
qf関数を使う。以下は、分子の自由度が1、分母の自由度が54の場合の下側1パーセント点(=0.000159…)、上側1パーセント点(=7.128819…)を求めた例。デフォルトでは下側パーセント点を返す。上側パーセント点を求めるには、lower.tailオプションをFALSEとする。
> qf(0.01, 1, 54)
[1] 0.0001585493
> qf(1 - 0.01, 1, 54)
[1] 7.128819
> qf(0.01, 1, 54, lower.tail = FALSE)
[1] 7.128819F分布におけるパーセント点を求める
> # 自由度5,7のF分布における、下側5パーセント点
> qf(0.05, 5, 7)
[1] 0.2050915
> # 自由度5,7のF分布における、上側5パーセント点
> qf(0.05, 5, 7, lower.tail = FALSE)
[1] 3.971523
> qf(1 - 0.05, 5, 7)
[1] 3.971523F分布におけるp値を求める
> # 自由度5,7のF分布における、確率変数が2のときの下側p値
> pf(2, 5, 7)
[1] 0.8043268
> # 自由度5,7のF分布における、確率変数が2のときの上側p値
> pf(2, 5, 7, lower.tail = FALSE)
[1] 0.1956732ガンマ関数の値を求める
gamma関数を使う。有名なガンマ関数の性質であるΓ(n) = (n - 1)!(n≧2,整数)について、
> gamma(1)
[1] 1
> gamma(2:5)
[1] 1 2 6 24となる。以下も有名な値(Γ(1/2)=√π)。