数値計算 - R入門【6/18更新】

目次

丸め誤差を考慮して数値の比較を行う

コンピューターは内部では浮動小数点演算を行っている都合上、丸め誤差は避けられない。それは実数同士の演算でよく見られる。

> (1 + 2) == 3
[1] TRUE
> (0.1 + 0.2) == 0.3
[1] FALSE
> print(sprintf("%.20f", 0.1 + 0.2))
[1] "0.30000000000000004441"
> print(sprintf("%.20f", 0.3))
[1] "0.29999999999999998890"

Rには標準でVisual BasicのDecimal型に相当するベクトルの型は存在せず、計算時に工夫する方法がある。

簡単に回避する方法としてsignif関数を使う方法がある。この関数は指定した有効数字を指定した桁まで丸めることができるため（デフォルトは6桁）、比較時にこの関数を使用すればよい。

> signif(0.1 + 0.2) == 0.3
[1] TRUE
> signif(0.1 + 0.2, digits = 16) == 0.3
[1] TRUE
> signif(0.1 + 0.2, digits = 17) == 0.3
[1] FALSE
> print(sprintf("%.20f", signif(0.1 + 0.2, digits = c(15, 16, 17, 18))))
[1] "0.29999999999999998890" "0.29999999999999998890" "0.30000000000000004441" "0.30000000000000004441"
> print(sprintf("%.20f", signif(0.3, digits = c(15, 16, 17, 18))))
[1] "0.29999999999999998890" "0.29999999999999998890" "0.29999999999999998890" "0.29999999999999998890"

ちなみに、round関数でも同様のことができるが、round関数とsignif関数ではdigitsオプションの意味が違うため注意。この手の処理でround関数を使うことは推奨しない。

> round(0.1 + 0.2, digits = 15) == 0.3
[1] TRUE
> round(0.1 + 0.2, digits = 16) == 0.3
[1] FALSE
> print(sprintf("%.20f", round(0.1 + 0.2, digits = 14:17)))
[1] "0.29999999999999998890" "0.29999999999999998890" "0.30000000000000004441" "0.30000000000000004441"
> print(sprintf("%.20f", round(0.3, digits = 14:17)))
[1] "0.29999999999999998890" "0.29999999999999998890" "0.29999999999999998890" "0.29999999999999998890"

丸め誤差を完全に自動でうまく処理できる方法はなく、その計算で求められる精度を基に、その都度工夫をする必要がある。

関数の最大値・最小値を得る

optim関数を使う。関数 f(x) = x ^ 2 - 5 の最小値を求めてみる。図からf(x)が最小となるのはx = 0でその時のf(x)は-5である。簡単な計算であれば、methodオプションはBFGSを指定する。計算には適当な初期値（この例では、f(x) が最小となるxの探索のための最初の値）を与える必要があり、以下の例では10としている。

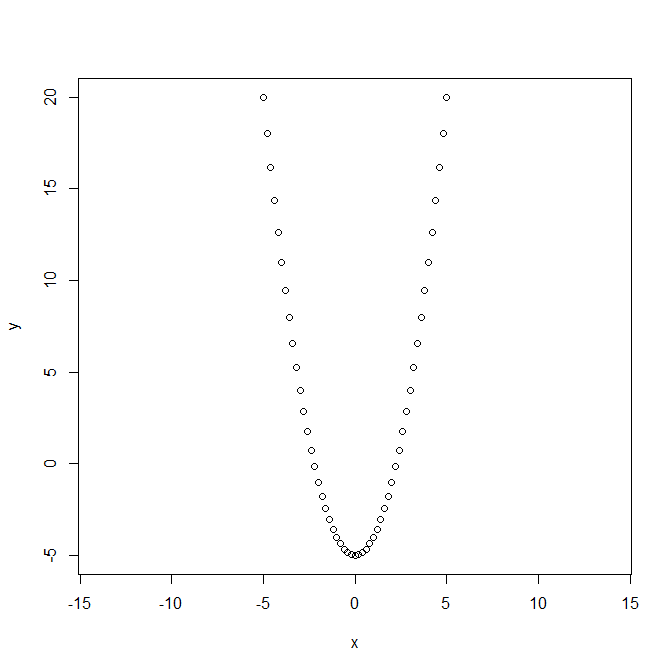
> f <- function(xf) xf ^ 2 - 5
> x <- seq(-5, 5, by = 0.2)
> y <- f(x)
> optim(10, f, method = "BFGS")
$par
[1] 2.441602e-11
$value
[1] -5
$counts
function gradient 
       6        3 
$convergence
[1] 0
$message
NULL

戻り値のparに最小となる関数の引数が、valueにはその最小となるf(x)値が格納されている。 逆に、関数の最大値を得るためには、controlオプションにリストとしてfnscaleに負の値を与える。以下の例では、関数f(x) = -(x ^ 2) - 5の最大値を求めており、図より、x=0の時に最大値f(x)=-5を得ることが明らかである。

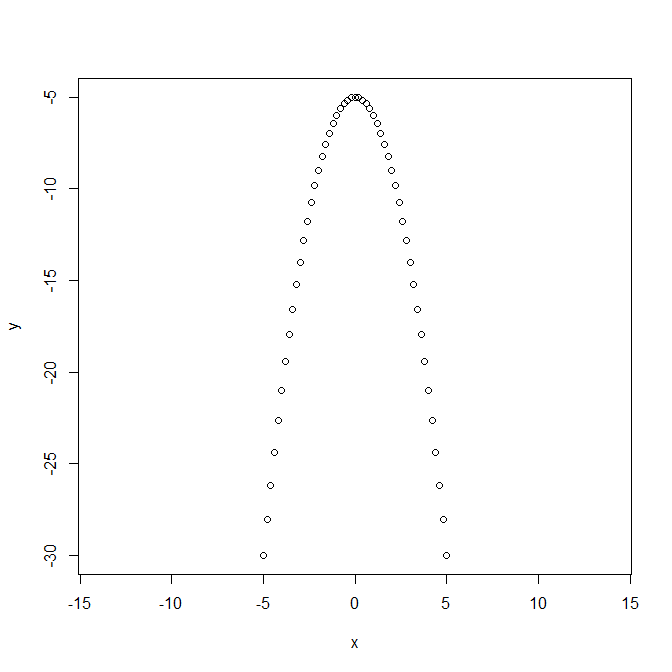
> f <- function(xf) -(xf ^ 2) - 5
> x <- seq(-5, 5, by = 0.2)
> y <- f(x)
> optim(10, f, control = list(fnscale = -1), method = "BFGS")
$par
[1] 2.441602e-11
$value
[1] -5
$counts
function gradient 
       6        3 
$convergence
[1] 0
$message
NULL

戻り値parに関数が最大となる場合の引数の値(=0)、その最大となった関数の値(=-5)が格納されている。

関数の最小値（最大値）を検索する

optimize関数を使う。以下は関数 f(x) = (x-2)^2 - 10 の最小値を検索した例。xの最小値は式と下図より10であり、その時の説明変数 x=2 である。戻り値はリストで、objectiveに最小値が、その時の説明変数の値がminimumに格納されている。

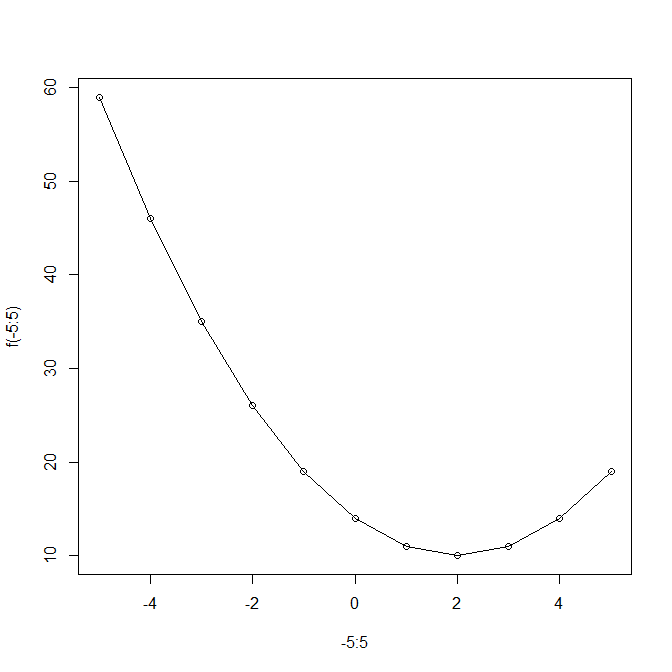
> f <- function(x) return((x - 2) ^ 2 + 10)
> plot(-5:5, f(-5:5), type = "o")
> optimize(f, c(-5, 5))
$minimum
[1] 2
$objective
[1] 10

以下は関数 f(x) = -(x-2)^2 - 10 の最大値を検索した例。xの最大値は式と下図より20であり、その時の説明変数 x=2 である。最大値を検索する場合はmaximumオプションをTRUEにする。

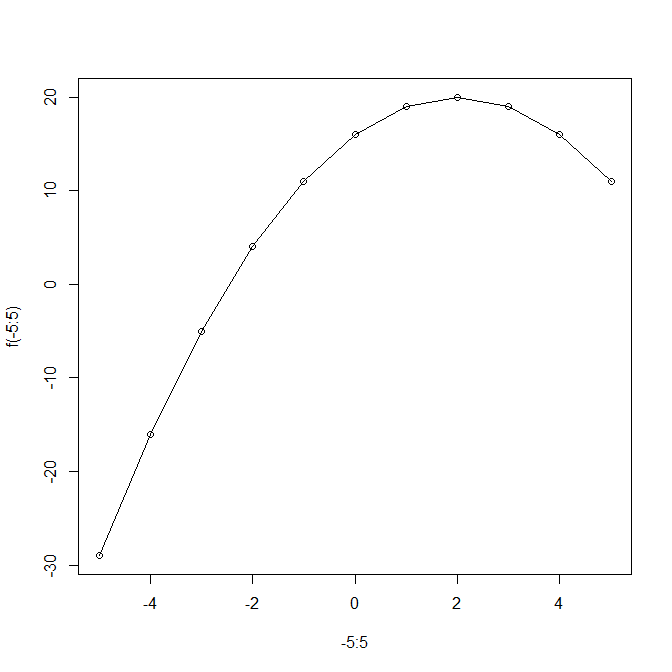
> f <- function(x) return(-(x - 2) ^ 2 + 20)
> plot(-5:5, f(-5:5), type = "o")
> optimize(f, c(-5, 5), maximum = TRUE)
$maximum
[1] 2
$objective
[1] 20

少しふざけて、上図の範囲（x > -5、x < 5）で最小値を検索してみる。2番目の引数に説明変数の検索範囲をベクトル（最小値、最大値）で与える。図のとおりに、説明変数がおおよそ-5のときにおおよそ-29であると求まる（グラフの左端のこと）。

> optimize(f, c(-5, 5))
$minimum
[1] -4.999944
$objective
[1] -28.99922

optimize関数の3番目以降の引数には、その検索を行う関数の引数を指定することができる。以下の例では検索する関数 f(x, a) であり、最小値検索のための説明変数はその関数の1番目にして、2番目以降は任意の値を設定することができる。

> f <- function(x, a) return((x - a) ^ 2 + 10)
> optimize(f, c(-5, 5), a = 2)
$minimum
[1] 2
$objective
[1] 10
> optimize(f, c(-5, 5), a = 3)
$minimum
[1] 3
$objective
[1] 10

複数の引数を持つ関数の値の最小値（最大値）を求める

optim関数を使う。使用時には適切な初期値を与える必要がある。数値的に求めるため、必ずしも期待通りの結果が得られるわけではないので注意。

以下はf1とf2というそれぞれ2つずつ引数を持つ関数の最小値と最大値を求めた例。f1の値が最小となるのはf1(5, 7)、f2の値が最大値となるのはf2(5, 7)であることは明らか。optim関数はデフォルトでは関数の値が最小値となる引数を求めるが、最大値となる引数を求めたい場合はcontrolオプションにlist(fnscale = -1)を指定すること。

> f1 <- function(x) {(x[1] - 5) ^ 2 + (x[2] - 7) ^ 2}
> f2 <- function(x) {-((x[1] - 5) ^ 2 + (x[2] - 7) ^ 2)}
> r <- optim(c(0, 0), f1, method = "BFGS")
> print(r)
$par
[1] 5 7
$value
[1] 1.31369e-22
$counts
function gradient 
      12        3 
$convergence
[1] 0
$message
NULL

f2関数の最小値は負の無限大であり、fnscaleに-1を指定しない状態では求めた引数（以下の$par）がまともに求まっていないことが明らか。fnscaleに-1を指定することで、期待通りの結果が得られる。

> r <- optim(c(0, 0), f2, method = "BFGS")
> print(r)
$par
[1] -4.758163e+13 -1.858368e+13
$value
[1] -2.609365e+27
$counts
function gradient 
      28       28 
$convergence
[1] 0
$message
NULL
> r <- optim(c(0, 0), f2, method = "BFGS", control = list(fnscale = -1))
> print(r)
$par
[1] 5 7
$value
[1] -1.31369e-22
$counts
function gradient 
      12        3 
$convergence
[1] 0
$message
NULL

サンプルデータを確認する

Rには、数値計算に使えるサンプルデータが標準で収録されている。標準で読み込まれるパッケージ（datasets）に多数含まれている。含まれているデータを確認するには、data関数を使う。

> data()

これらのデータはそのまますぐに使うことができる。

> AirPassengers
     Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1949 112 118 132 129 121 135 148 148 136 119 104 118
1950 115 126 141 135 125 149 170 170 158 133 114 140
1951 145 150 178 163 172 178 199 199 184 162 146 166
（以下、表示省略）

パスカルの三角形を求める

以下のスクリプトを実行する。1～12のパスカルの三角形を求めている。

for (i in 1:12) {
  cat(sprintf("%2d: ", i))
  for (j in 0:i) {
    cat(sprintf("%3d ", choose(i, j)))
  }
  cat("\n")
}

出力

1:   1   1 
 2:   1   2   1 
 3:   1   3   3   1 
 4:   1   4   6   4   1 
 5:   1   5  10  10   5   1 
 6:   1   6  15  20  15   6   1 
 7:   1   7  21  35  35  21   7   1 
 8:   1   8  28  56  70  56  28   8   1 
 9:   1   9  36  84 126 126  84  36   9   1 
10:   1  10  45 120 210 252 210 120  45  10   1 
11:   1  11  55 165 330 462 462 330 165  55  11   1 
12:   1  12  66 220 495 792 924 792 495 220  66  12   1

回帰分析における対数尤度を簡単に求める

回帰分析をlm関数で行い、その戻り値を用いてlogLik関数を使う。以下は「情報量規準」（朝倉書店）に掲載の計算例（pp.59-61）を再現した結果。

観測値はpp.59-60に掲載されており、以下のとおり。これをtable_p059.csvと保存する。

i,    x,     y
 1, 0.00, 0.854
 2, 0.05, 0.786
 3, 0.10, 0.706
 4, 0.15, 0.763
 5, 0.20, 0.772
 6, 0.25, 0.693
 7, 0.30, 0.805
 8, 0.35, 0.739
 9, 0.40, 0.760
10, 0.45, 0.764
11, 0.50, 0.810
12, 0.55, 0.791
13, 0.60, 0.798
14, 0.65, 0.841
15, 0.70, 0.882
16, 0.75, 0.879
17, 0.80, 0.863
18, 0.85, 0.934
19, 0.90, 0.971
20, 0.95, 0.985

以下、計算結果。当該書籍では、上記の観測値を用いた多項式回帰モデルの残差分散と対数尤度の一覧を表にまとめて掲載している（p.61）。

> dtf <- read.csv("table_p059.csv", header = TRUE)
> n <- nrow(dtf)
> for (k in 1:9) {
+     r <- lm(y ~ poly(x, k), data = dtf)
+     rss <- sum(r$re ^ 2)
+     cat(sprintf("次数:%d, 残差分散:%8.6f, 対数尤度:%5.2f\n", k, rss / n, logLik(r)))
+ }
次数:1, 残差分散:0.002587, 対数尤度:31.19
次数:2, 残差分散:0.000922, 対数尤度:41.51
次数:3, 残差分散:0.000833, 対数尤度:42.52
次数:4, 残差分散:0.000737, 対数尤度:43.75
次数:5, 残差分散:0.000688, 対数尤度:44.44
次数:6, 残差分散:0.000650, 対数尤度:45.00
次数:7, 残差分散:0.000622, 対数尤度:45.44
次数:8, 残差分散:0.000607, 対数尤度:45.69
次数:9, 残差分散:0.000599, 対数尤度:45.83

回帰分析におけるAICを簡単に求める

回帰分析をlm関数で行い、その戻り値を用いてAIC関数を使う。以下は「情報量規準」（朝倉書店）に掲載の計算例（pp.59-61）を再現した結果。

観測値はpp.59-60に掲載されており、以下のとおり。これをtable_p059.csvと保存する。

i,    x,     y
 1, 0.00, 0.854
 2, 0.05, 0.786
 3, 0.10, 0.706
 4, 0.15, 0.763
 5, 0.20, 0.772
 6, 0.25, 0.693
 7, 0.30, 0.805
 8, 0.35, 0.739
 9, 0.40, 0.760
10, 0.45, 0.764
11, 0.50, 0.810
12, 0.55, 0.791
13, 0.60, 0.798
14, 0.65, 0.841
15, 0.70, 0.882
16, 0.75, 0.879
17, 0.80, 0.863
18, 0.85, 0.934
19, 0.90, 0.971
20, 0.95, 0.985

以下、計算結果。当該書籍では、上記の観測値を用いた多項式回帰モデルの残差分散とAICの一覧を表にまとめて掲載している（p.61）。

> dtf <- read.csv("table_p059.csv", header = TRUE)
> n <- nrow(dtf)
> for (k in 1:9) {
+     r <- lm(y ~ poly(x, k), data = dtf)
+     rss <- sum(r$re ^ 2)
+     cat(sprintf("次数:%d, 残差分散:%8.6f, AIC:%5.2f\n", k, rss / n, AIC(r)))
+ }
次数:1, 残差分散:0.002587, AIC:-56.38
次数:2, 残差分散:0.000922, AIC:-75.03
次数:3, 残差分散:0.000833, AIC:-75.04
次数:4, 残差分散:0.000737, AIC:-75.50
次数:5, 残差分散:0.000688, AIC:-74.89
次数:6, 残差分散:0.000650, AIC:-74.00
次数:7, 残差分散:0.000622, AIC:-72.89
次数:8, 残差分散:0.000607, AIC:-71.38
次数:9, 残差分散:0.000599, AIC:-69.66

回帰モデルの信頼区間と予測区間

lm関数により求めた回帰モデルの信頼区間と予測区間はpredict関数で求めることができる。以下の計算により、赤実線が求めた回帰直線。桃破線がその95%信頼区間、橙点線がその95%予測区間。

> # 説明変数xと目的変数y
> x <- c(1, 2, 3, 5, 6, 7, 8, 10, 11, 12)
> y <- c(0, 1, 1, 2, 4, 4, 6,  5,  8,  8)
> # 回帰直線を求める
> r <- lm(y ~ x)
> print(r)
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept)            x  
    -0.8567       0.7318  
> # yの推定値
> yest <- fitted(r)
> # 信頼区間と予測区間の計算(後続の手順のためdata.frame化)
> dtf <- data.frame(x)
> rcon <- predict(r, dtf, interval = "confidence", level = 0.95)
> rpre <- predict(r, dtf, interval = "prediction", level = 0.95)
> rcon <- data.frame(rcon)
> rpre <- data.frame(rpre)
> # 図の作成(黒丸:観測値,赤実線:回帰直線,桃破線:信頼区間,橙点線:予測区間)
> plot(x, y, type = "n", asp = 1.0)
> lines(x, rpre$lwr, lty = "dotted", col = "orange", lwd = 2.0)
> lines(x, rpre$upr, lty = "dotted", col = "orange", lwd = 2.0)
> lines(x, rcon$lwr, lty = "dashed", col = "pink", lwd = 2.0)
> lines(x, rcon$upr, lty = "dashed", col = "pink", lwd = 2.0)
> lines(x, yest, col = "red", lwd = 2.0)
> points(x, y, pch = 20, col = "black")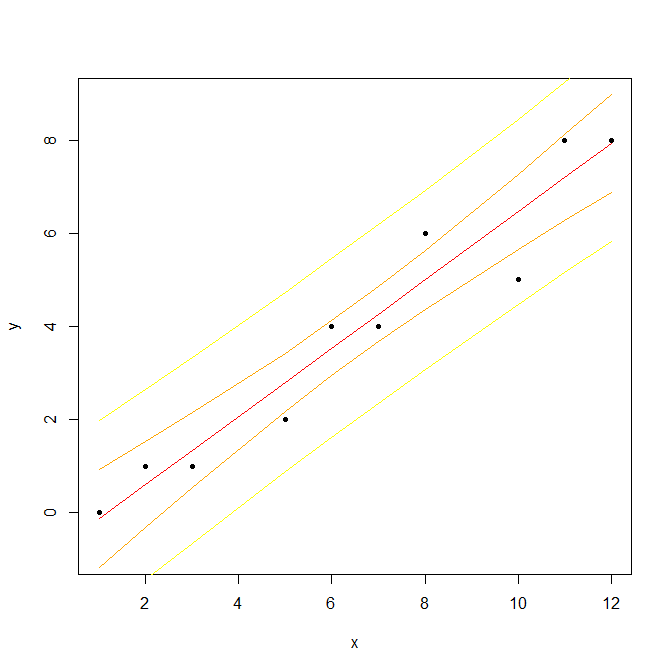

> # 以下はpredict関数と手計算の計算結果の比較
> ah <- 0.95
> n <- length(x)
> k <- 2
> mxxx <- matrix(c(rep(1, n), x), ncol = 2)
> mxy <- matrix(y, ncol = 1)
> # 最小二乗推定量
> mxb <- solve(t(mxxx) %*% mxxx) %*% (t(mxxx) %*% mxy)
> print(mxb)
           [,1]
[1,] -0.8567050
[2,]  0.7318008
> # yの推定値
> yest <- mxxx %*% mxb
> # 残差分散
> s <- sqrt(sum((y - yest) ^ 2) / (n - k))
> #
> s0 <- sh0 <- double(n)
> for (i in 1:n) {
+ mxx0 <- matrix(c(1, x[i]), ncol = 1)
+ s0[i] <- s * sqrt(t(mxx0) %*% solve(t(mxxx) %*% mxxx) %*% mxx0)
+ sh0[i] <- s * sqrt(1 + t(mxx0) %*% solve(t(mxxx) %*% mxxx) %*% mxx0)
+ }
> # 95%信頼区間
> ycon1 <- yest - s0 * qt((1. - ah) / 2, n - k, lower.tail = FALSE)
> ycon2 <- yest + s0 * qt((1. - ah) / 2, n - k, lower.tail = FALSE)
> # 95%予測区間
> ypre1 <- yest - sh0 * qt((1. - ah) / 2, n - k, lower.tail = FALSE)
> ypre2 <- yest + sh0 * qt((1. - ah) / 2, n - k, lower.tail = FALSE)
> # predict関数による信頼区間と予測区間
> print(data.frame(rcon$lwr, rcon$upr, rpre$lwr, rpre$upr))
     rcon.lwr  rcon.upr   rpre.lwr  rpre.upr
1  -1.1763909 0.9265825 -2.2315171  1.981709
2  -0.3152118 1.5290049 -1.4382140  2.652007
3   0.5349489 2.1424457 -0.6558465  3.333241
4   2.1772621 3.4273356  0.8728263  4.731771
5   2.9513451 4.1168542  1.6179064  5.450293
6   3.6831458 4.8486549  2.3497072  6.182094
7   4.3726644 5.6227379  3.0682286  6.927174
8   5.6575543 7.2650511  4.4667589  8.455846
9   6.2709951 8.1152118  5.1479929  9.238214
10  6.8734175 8.9763909  5.8182913 10.031517
> # 手計算による信頼区間と予測区間
> print(data.frame(ycon1, ycon2, ypre1, ypre2))
        ycon1     ycon2      ypre1     ypre2
1  -1.1763909 0.9265825 -2.2315171  1.981709
2  -0.3152118 1.5290049 -1.4382140  2.652007
3   0.5349489 2.1424457 -0.6558465  3.333241
4   2.1772621 3.4273356  0.8728263  4.731771
5   2.9513451 4.1168542  1.6179064  5.450293
6   3.6831458 4.8486549  2.3497072  6.182094
7   4.3726644 5.6227379  3.0682286  6.927174
8   5.6575543 7.2650511  4.4667589  8.455846
9   6.2709951 8.1152118  5.1479929  9.238214
10  6.8734175 8.9763909  5.8182913 10.031517

計算機イプシロンを求める

計算機イプシロンとは、不等式「1 + epsm > 1」が成り立つ最小の正数epsmのこと。これを手計算で求めてみる。

> epsm <- 1.0
> while (1.0 + epsm > 1.0) {
+     epsm <- epsm / 2.0
+ }
> epsm <- epsm * 2.0
> print(epsm)
[1] 2.220446e-16

この環境下では、約2.2×10 ^-16 であることがわかる。なお、Rにはあらかじめ稼働環境の計算能力の値を格納したリスト.Machineがグローバル変数として定義されており、これに含まれるdouble.epsが計算機イプシロンである。

> .Machine$double.eps
[1] 2.220446e-16

手計算の計算結果と矛盾がないことがわかる。

重み付き線形最小二乗法を行う

lm関数を使う。weightsオプションに重みを指定すると、その重みを考慮した計算を行う。

以下の例では、与えられた8組の測定値を使用して、線形最小二乗法により回帰モデルy = b1 + b2 * x + b3 * x ^ 2（b1, b2, b3は回帰係数）を作成した例。重み無し、重み付きでそれぞれ計算している。図を見てのとおり、重みを考慮しないモデル（青実線）は全点の近くをまんべんなく通っているが、重みを考慮したモデル（x = 3, 6のみ重みが他の100倍、赤実線）は、x = 3, 6の測定値を無理矢理通るようなモデル（回帰係数）が求められていることがわかる。

> # 計算の準備
> x <- c(1, 2, 3, 5, 6, 7, 8, 9)
> y <- c(1, 4, 10, 25, 32, 49, 64, 75)  # 測定値（図の黒丸）
> w <- rep(1, length(x))
> w[c(3, 5)] <- 100
> print(data.frame(x, y, w))
  x  y   w
1 1  1   1
2 2  4   1
3 3 10 100
4 5 25   1
5 6 32 100
6 7 49   1
7 8 64   1
8 9 75   1
> 
> # 重みを考慮しない計算（図の青実線）
> r1 <- lm(y ~ 1 + x + I(x ^ 2))
> print(r1)
Call:
lm(formula = y ~ 1 + x + I(x^2))
Coefficients:
(Intercept)            x       I(x^2)  
    -0.6731       0.7042       0.8792  
> sm <- summary(r1)
> print(sm)
Call:
lm(formula = y ~ 1 + x + I(x^2))
Residuals:
       1        2        3        4        5        6        7        8 
 0.08963 -0.25225  0.64741  0.17136 -3.20434  1.66150  2.76888 -1.88219 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)  -0.6731     2.8545  -0.236  0.82295   
x             0.7042     1.3677   0.515  0.62859   
I(x^2)        0.8792     0.1351   6.507  0.00128 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.225 on 5 degrees of freedom
Multiple R-squared:  0.9954,    Adjusted R-squared:  0.9936 
F-statistic: 546.6 on 2 and 5 DF,  p-value: 1.399e-06
> print(r1)                              # lm関数による計算結果の概要
Call:
lm(formula = y ~ 1 + x + I(x^2))
Coefficients:
(Intercept)            x       I(x^2)  
    -0.6731       0.7042       0.8792  
> print(sm$coef)                         # 推定した回帰係数,その標準誤差,t値,p値
              Estimate Std. Error    t value    Pr(>|t|)
(Intercept) -0.6730552  2.8545448 -0.2357837 0.822953999
x            0.7041995  1.3677286  0.5148679 0.628589629
I(x^2)       0.8792277  0.1351261  6.5067205 0.001280624
> print(sum(sm$resi ^ 2))                # 残差平方和
[1] 24.75789
> print(sum((y - fitted(r1)) ^ 2))
[1] 24.75789
> print(sm$df)                           # モデルのランク,自由度,回帰係数の数
[1] 3 5 3
> print(sum(sm$resi ^ 2) / sm$df[2])     # 残差分散
[1] 4.951578
> print(sm$sigma)                        # 回帰値の標準誤差
[1] 2.225214
> print(sm$sigma ^ 2 * sm$cov.unscaled)  # 推定した回帰係数の分散共分散行列
            (Intercept)          x      I(x^2)
(Intercept)   8.1484260 -3.5141134  0.31168334
x            -3.5141134  1.8706816 -0.18061352
I(x^2)        0.3116833 -0.1806135  0.01825906
> 
> # 重みを考慮した計算（図の赤実線）
> r2 <- lm(y ~ 1 + x + I(x ^ 2), weights = w)
> print(r2)
Call:
lm(formula = y ~ 1 + x + I(x^2), weights = w)
Coefficients:
(Intercept)            x       I(x^2)  
      8.024       -2.828        1.143  
> sm <- summary(r2)
> print(sm)
Call:
lm(formula = y ~ 1 + x + I(x^2), weights = w)
Weighted Residuals:
     1      2      3      4      5      6      7      8 
-5.340 -2.942  1.701  2.535 -2.128  4.754  5.433 -0.173 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)   8.0244     3.7465   2.142  0.08512 . 
x            -2.8277     1.8037  -1.568  0.17773   
I(x^2)        1.1432     0.1958   5.839  0.00208 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.542 on 5 degrees of freedom
Multiple R-squared:  0.9966,    Adjusted R-squared:  0.9953 
F-statistic: 734.5 on 2 and 5 DF,  p-value: 6.701e-07
> print(r2)                              # lm関数による計算結果の概要
Call:
lm(formula = y ~ 1 + x + I(x^2), weights = w)
Coefficients:
(Intercept)            x       I(x^2)  
      8.024       -2.828        1.143  
> print(sm$coef)                         # 推定した回帰係数,その標準誤差,t値,p値
             Estimate Std. Error   t value    Pr(>|t|)
(Intercept)  8.024356  3.7464592  2.141851 0.085117824
x           -2.827713  1.8037101 -1.567721 0.177732033
I(x^2)       1.143186  0.1957718  5.839381 0.002083779
> print(sum(sm$resi ^ 2))                # 残差平方和
[1] 103.1604
> print(sum(w * (y - fitted(r2)) ^ 2))
[1] 103.1604
> print(sm$df)                           # モデルのランク,自由度,回帰係数の数
[1] 3 5 3
> print(sum(sm$resi ^ 2) / sm$df[2])     # 残差分散
[1] 20.63208
> print(sm$sigma)                        # 回帰値の標準誤差
[1] 4.542255
> print(sm$sigma ^ 2 * sm$cov.unscaled)  # 推定した回帰係数の分散共分散行列
            (Intercept)          x      I(x^2)
(Intercept)  14.0359563 -6.6722356  0.70866822
x            -6.6722356  3.2533702 -0.35090188
I(x^2)        0.7086682 -0.3509019  0.03832661
> 
> # 図の描画
> plot(x, fitted(r1), type = "l", col = "blue", xlab = "x", ylab = "y")
> lines(x, fitted(r2), col = "red")
> points(x, y, pch = 20)

重み付き非線形最小二乗法を行う

nls関数を使う。weightsオプションに重みを指定すると、その重みを考慮した計算を行う。

以下の例では、与えられた8組の測定値を使用して、非線形最小二乗法により回帰モデルy = b1 + b2 * x * exp(b3 * x)（b1, b2, b3は回帰係数）を作成した例。重み無し、重み付きでそれぞれ計算している。図を見てのとおり、重みを考慮しないモデル（青実線）は全点の近くをまんべんなく通っているが、重みを考慮したモデル（x = 3, 6のみ重みが他の100倍、赤実線）は、x = 3, 6の測定値を無理矢理通るようなモデル（回帰係数）が求められていることがわかる。

> # 計算の準備
> x <- c(1, 2, 3, 5, 6, 7, 8, 9)
> y <- c(1, 4, 10, 25, 32, 49, 64, 75)  # 測定値（図の黒丸）
> w <- rep(1, length(x))
> w[c(3, 5)] <- 100
> dtf <- data.frame(x, y, w)
> print(dtf)
  x  y   w
1 1  1   1
2 2  4   1
3 3 10 100
4 5 25   1
5 6 32 100
6 7 49   1
7 8 64   1
8 9 75   1
> f <- function(x, b) b[1] + b[2] * x * exp(b[3] * x)
> b0 <- c(1, 1, 1)
> 
> # 重みを考慮しない計算（図の青実線）
> r1 <- nls(y ~ f(x, b), start = list(b = b0))
> sm <- summary(r1)
> print(sm)       # nls関数による計算結果の概要
Formula: y ~ f(x, b)
Parameters:
   Estimate Std. Error t value Pr(>|t|)   
b1 -3.89078    2.46437  -1.579  0.17521   
b2  3.39494    0.74297   4.569  0.00601 **
b3  0.10847    0.02318   4.679  0.00544 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.502 on 5 degrees of freedom
Number of iterations to convergence: 21 
Achieved convergence tolerance: 3.21e-06
> print(sm$coef)  # 推定した回帰係数,その標準誤差,t値,p値
     Estimate Std. Error   t value    Pr(>|t|)
b1 -3.8907795 2.46436971 -1.578813 0.175211732
b2  3.3949412 0.74297094  4.569413 0.006005113
b3  0.1084657 0.02318143  4.678990 0.005438508
> print(sum(sm$resi ^ 2))                # 残差平方和
[1] 31.30051
> print(sum((y - fitted(r1)) ^ 2))
[1] 31.30051
> print(sm$df)                           # 推定した回帰係数の数と自由度
[1] 3 5
> print(sum(sm$resi ^ 2) / sm$df[2])     # 残差分散
[1] 6.260101
> print(sm$sigma)                        # 回帰値の標準誤差
[1] 2.502019
> print(sm$sigma ^ 2 * sm$cov.unscaled)  # 推定した回帰係数の分散共分散行列
            b1          b2            b3
b1  6.07311807 -1.56568510  0.0449342593
b2 -1.56568510  0.55200581 -0.0170136719
b3  0.04493426 -0.01701367  0.0005373789
> 
> # 重みを考慮した計算（図の赤実線）
> r2 <- nls(y ~ f(x, b), weights = w, start = list(b = b0))
> sm <- summary(r2)
> print(sm)       # nls関数による計算結果の概要
Formula: y ~ f(x, b)
Parameters:
   Estimate Std. Error t value Pr(>|t|)    
b1 -0.03045    1.18131  -0.026 0.980435    
b2  2.06079    0.33571   6.139 0.001666 ** 
b3  0.15929    0.02080   7.659 0.000604 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.741 on 5 degrees of freedom
Number of iterations to convergence: 14 
Achieved convergence tolerance: 3.676e-06
> print(sm$coef)  # 推定した回帰係数,その標準誤差,t値,p値
      Estimate Std. Error     t value     Pr(>|t|)
b1 -0.03044686 1.18131366 -0.02577373 0.9804348365
b2  2.06079018 0.33571296  6.13854825 0.0016664488
b3  0.15929178 0.02079896  7.65864353 0.0006043864
> print(sum(sm$resi ^ 2))                # 残差平方和
[1] 69.95679
> print(sum(w * (y - fitted(r2)) ^ 2))
[1] 69.95679
> print(sm$df)                           # 推定した回帰係数の数と自由度
[1] 3 5
> print(sum(sm$resi ^ 2) / sm$df[2])     # 残差分散
[1] 13.99136
> print(sm$sigma)                        # 回帰値の標準誤差
[1] 3.740502
> print(sm$sigma ^ 2 * sm$cov.unscaled)  # 推定した回帰係数の分散共分散行列
            b1           b2            b3
b1  1.39550197 -0.371789063  0.0219612500
b2 -0.37178906  0.112703189 -0.0069215507
b3  0.02196125 -0.006921551  0.0004325965
> 
> # 図の描画
> plot(x, fitted(r1), type = "l", col = "blue", xlab = "x", ylab = "y")
> lines(x, fitted(r2), col = "red")
> points(x, y, pch = 20)

複数のパラメーターと定数を持つ関数の値が最大・最小となるパラメーターを求める

optim関数を使う。第一引数にパラメーターの初期値を、第二引数に関数を指定する。関数に与えたい定数は、関数の引数に作成しておく。

optim(パラメーターの初期値, 関数, …)

以下は、自作関数fの値が最大・最小となるパラメーターを求めた例。この例では、パラメーター（未知数）は2個（ベクトルd）、関数を決める定数はc1とc2の2個。optim関数はデフォルトでは関数の値が最小となるパラメーターを推定する。推定するパラメーター（$par）は数値的に解いて求めているため、必ずしも切りのよい値にはならないことに注意。

> f <- function(d, c1, c2) {(d[1] - (c1 + c2)) ^ 2 + (d[2] - c1) ^ 4 - 2}
> optim(c(0, 0), f, method = "BFGS", c1 = 1, c2 = 2)
$par
[1] 2.999486 0.966386
$value
[1] -1.999998
$counts
function gradient 
      19       16 
$convergence
[1] 0
$message
NULL
> f(c(3, 1), 1, 2)
[1] -2
> optim(c(0, 0), f, method = "BFGS", c1 = 3, c2 = 1)
$par
[1] 3.999491 2.969365
$value
[1] -1.999999
$counts
function gradient 
      24       21 
$convergence
[1] 0
$message
NULL
> f(c(4, 3), 3, 1)
[1] -2

関数の値が最大となるパラメーターを求めたい場合は、controlオプションに「list(fnscale = -1)」と指定すればよい。

> f <- function(d, c1, c2) {-((d[1] - (c1 + c2)) ^ 2 + (d[2] - c1) ^ 4 - 2)}
> optim(c(0, 0), f, control = list(fnscale = -1), method = "BFGS", c1 = 1, c2 = 1)
$par
[1] 2.0003449 0.9741651
$value
[1] 1.999999
$counts
function gradient 
      24       21 
$convergence
[1] 0
$message
NULL

時系列にチェビシェフI型のローパスフィルターを使う

signalパッケージのcheby1関数とfiltfilt関数を使う。以下は、200Hzでサンプリングされた正弦波の和から構成される入力信号（周波数は1Hzと10Hzをもつ）を作成し、その入力信号から5Hz以下の周波数をカットした例。

> library(signal)                        # signalパッケージの読み込み
> fs <- 200                              # サンプリング周波数(Hz)
> x <- seq(0, 5, by = 1 / fs)            # 時刻
> yi <- sin(2 * pi * 1 * x) + 0.7 * sin(2 * pi * 10 * x)  # 入力信号
> od <- 4                                # フィルターの次数
> rp <- 1                                # 通過帯域リップル(dB)
> fc <- 5                                # カットオフ周波数(Hz)
> wp <- fc / (fs / 2)                    # 通過帯域エッジ周波数(Hz)
> r <- cheby1(od, rp, wp, type = "low")  # フィルターの設計
> yo <- filtfilt(r, yi)                  # フィルターの実行
> plot(x, yi, type = "l", col = "cyan")
> lines(x, yo, col = "blue")
> legend("topright", legend = c("入力", "出力"), col = c("cyan", "blue"), lty = 1)