R入門
入門 統計解析 [医学・自然科学編](東京図書)
最終更新:
r-intro
-
view
目次
t分布のパーセント点の略表(両側)
> for (i in 1:20) {
+ cat(sprintf("%2d %5.3f %6.3f %6.3f\n", i, qt(0.95, i), qt(0.975, i), qt(0.995, i)))
+ }
1 6.314 12.706 63.657
2 2.920 4.303 9.925
3 2.353 3.182 5.841
4 2.132 2.776 4.604
5 2.015 2.571 4.032
6 1.943 2.447 3.707
7 1.895 2.365 3.499
8 1.860 2.306 3.355
9 1.833 2.262 3.250
10 1.812 2.228 3.169
11 1.796 2.201 3.106
12 1.782 2.179 3.055
13 1.771 2.160 3.012
14 1.761 2.145 2.977
15 1.753 2.131 2.947
16 1.746 2.120 2.921
17 1.740 2.110 2.898
18 1.734 2.101 2.878
19 1.729 2.093 2.861
20 1.725 2.086 2.845ガンマ関数の値の計算(pp.120-121)
ガンマ関数の値を得るにはgamma関数を使う。
> alpha <- seq(0.1, 3.0, 0.1)
> ggamma <- gamma(alpha)
> dtf <- data.frame(alpha, ggamma)
> print(dtf)
alpha ggamma
1 0.1 9.5135077
2 0.2 4.5908437
3 0.3 2.9915690
4 0.4 2.2181595
5 0.5 1.7724539
6 0.6 1.4891922
7 0.7 1.2980553
8 0.8 1.1642297
9 0.9 1.0686287
10 1.0 1.0000000
11 1.1 0.9513508
12 1.2 0.9181687
13 1.3 0.8974707
14 1.4 0.8872638
15 1.5 0.8862269
16 1.6 0.8935153
17 1.7 0.9086387
18 1.8 0.9313838
19 1.9 0.9617658
20 2.0 1.0000000
21 2.1 1.0464858
22 2.2 1.1018025
23 2.3 1.1667119
24 2.4 1.2421693
25 2.5 1.3293404
26 2.6 1.4296246
27 2.7 1.5446858
28 2.8 1.6764908
29 2.9 1.8273551
30 3.0 2.0000000
> plot(alpha, ggamma, type = "n")
> lines(alpha, ggamma)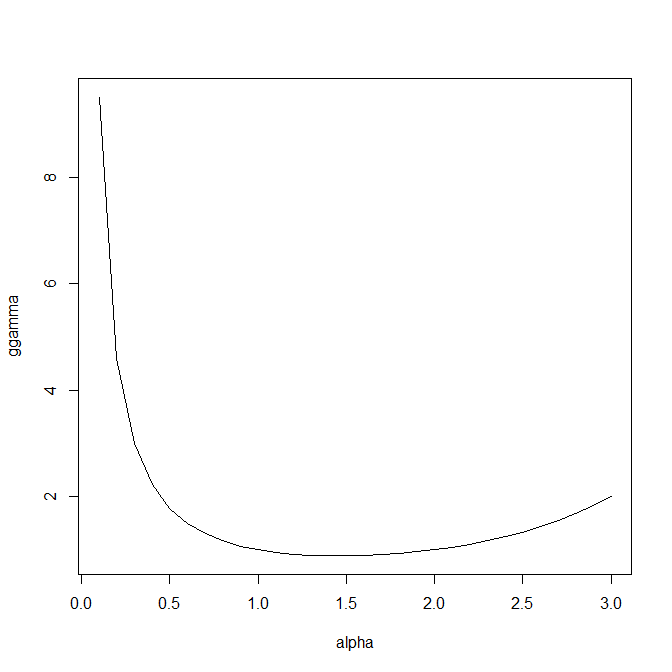
例 10.1 単回帰分析(pp.236-237)
本計算に使用するデータは、以下のとおり(p.236)。
i, x, y
1, 7, 6
2, 7, 9
3, 12, 10
4, 11, 13
5, 10, 13
6, 5, 7
7, 9, 11
8, 11, 14
9, 11, 15
10, 12, 7
11, 11, 13
12, 15, 14
13, 14, 10
14, 16, 16
15, 8, 8
16, 2, 8
17, 14, 8
18, 8, 12
19, 12, 16
20, 16, 12これをメモ帳に貼り付けてファイル「table10_1.csv」で保存し、カレントディレクトリに置いておく。
> dtf <- read.csv("table10_1.csv", header = TRUE)
> xi <- dtf$x
> yi <- dtf$y
> n <- nrow(dtf)
> p <- 2
> xm <- mean(xi)
> ym <- mean(yi)
> ssx2 <- sum((xi - xm) ^ 2)
> ssy2 <- sum((yi - ym) ^ 2)
> ssxy <- sum((xi - xm) * (yi - ym))
> b1 <- ssxy / ssx2
> b0 <- ym - b1 * xm
> yti <- b0 + b1 * xi
> sssse <- sum((yi - yti) ^ 2)
> sh2 <- sssse / (n - p)
> se <- sqrt(sh2)
> seb1 <- sqrt(sh2 / sum((xi - xm) ^ 2))
> tb1 <- b1 / seb1
> cat(sprintf("回帰式 y~ = %.4fx + %.3f\n", b1, b0))
回帰式 y~ = 0.4468x + 6.387
> cat(sprintf("誤差分散σ2の不偏推定量 σ2^ = %.2f \n", sh2))
誤差分散σ2の不偏推定量 σ2^ = 7.61
> cat(sprintf("回帰値の標準誤差 s.e. = %.2f\n", se))
回帰値の標準誤差 s.e. = 2.76
> cat(sprintf("β1の推定値の標準誤差 s.e.(b1) = %.3f \n", seb1))
β1の推定値の標準誤差 s.e.(b1) = 0.173
> cat(sprintf("β1の推定値のt値 t(b1) = %.2f \n", tb1))
β1の推定値のt値 t(b1) = 2.59
> cat(sprintf("t0.025(18) = %.2f\n", qt(1 - 0.025, n - p)))
t0.025(18) = 2.10例 10.5 一般線形モデルによる表現(pp.260-261)
本計算に使用するデータは、この書籍のオフィシャルページからダウンロードできる1-8a.csv。以下に転記。
番号,年齢,血圧,肺活量
1,22,110,4300
2,23,128,4500
3,24,104,3900
4,25,112,3000
5,27,108,4800
6,28,126,3800
7,28,126,3800
8,29,104,4000
9,30,125,3600
10,31,120,3400
11,32,116,3600
12,32,124,3900
13,33,106,3100
14,33,134,2900
15,34,128,4100
16,36,128,3420
17,37,116,3800
18,37,132,4150
19,38,134,2700
20,39,116,4550
21,40,120,2900
22,42,130,3950
23,46,126,3100
24,49,140,3000
25,50,156,3400
26,53,124,3400
27,56,118,3470
28,58,144,2800
29,64,142,2500
30,65,144,2350これをファイル1-8a.csvに保存し、ファイルをカレントディレクトリに置いた状態で以下のコマンドを実施。
> dtf <- read.csv("1-8a.csv", header = TRUE)
> n <- nrow(dtf)
> yi <- dtf[, 2]
> x1i <- dtf[, 3]
> x2i <- dtf[, 4]
> p <- 2
> degf <- n - p - 1
> mxy <- matrix(yi, ncol = 1)
> mxxx <- cbind(matrix(rep(1, n), ncol = 1), matrix(c(x1i, x2i), ncol = 2))
> mxb <- solve(t(mxxx) %*% mxxx) %*% t(mxxx) %*% mxy
> b <- as.vector(mxb)
> ssss <- sum((mxy - mxxx %*% mxb) ^ 2)
> sh2 <- ssss / degf
> mxcc <- sh2 * solve(t(mxxx) %*% mxxx)
> se <- sqrt(diag(mxcc))
> cat("回帰係数 b\n")
回帰係数 b
> print(b)
[1] 11.875986749 0.427751260 -0.007679603
> cat("誤差分散の不偏推定量 σ^2\n")
誤差分散の不偏推定量 σ^2
> print(sh2)
[1] 71.98984
> cat("分散共分散行列 Cov(b)\n")
分散共分散行列 Cov(b)
> print(mxcc)
[,1] [,2] [,3]
[1,] 591.40996325 -3.1826686561 -5.427955e-02
[2,] -3.18266866 0.0199042110 1.979321e-04
[3,] -0.05427955 0.0001979321 8.361641e-06
> cat("b の標準誤差 s.e.\n")
b の標準誤差 s.e.
> print(se)
[1] 24.31892192 0.14108228 0.00289165