非公式チュートリアル16 リズム4 ブライアン・ファーニホウのリズム分析と模倣3
このアーティクルは以下の論文の例を引用しています。
ミハイル・マルト「ブライアン・ファーニホウの音楽言語におけるいくつかの考察」The OM composer's book 第2巻より
ミハイル・マルト「ブライアン・ファーニホウの音楽言語におけるいくつかの考察」The OM composer's book 第2巻より
This article is quoted the original examples from;
Mikhail Malt: Some considerations on Brian Ferneyhough's musical language
The OM composer's book. 2 (ed. Delatour, IRCAM), page 7-19
Mikhail Malt: Some considerations on Brian Ferneyhough's musical language
The OM composer's book. 2 (ed. Delatour, IRCAM), page 7-19
この章は前回からのマルトの論文の続きだが、論文本文では「このようなやり方もある」と言った結果の説明だけで、その計算に至る過程のパッチは掲載されていない。よって今回は筆者(Imahori)がマルトの論文を元にパッチを再構成したものである。
まずマルトの論文で語られているのは、以下の2つのリズムツリー
(((4 4) (1 2 (5 (1 1 1 1)))) ((4 4) ((1 (-2 2 -3)) 1 (3 (1 1 1 -3)))))
(((4 4) (3 4 (6 (2 1 3 1)))) ((4 4) ((3 (4 3 -2)) 1 (5 (3 2 1 -1)))))
(((4 4) (3 4 (6 (2 1 3 1)))) ((4 4) ((3 (4 3 -2)) 1 (5 (3 2 1 -1)))))
を基として、その各数字の部分を見比べ、その数値の間でインターポレーションを行うとされる。
(インターポレーションは内挿とも言い、例えば1から3まで5回インターポレーションを行うと(1 1.5 2 2.5 3)というリストが得られる。これは和音の推移などにも応用できるが、今回はリズムに応用させる。)
例えば上の例だと、最初の(4 4)は4分の4拍子を指しているので無視し、1と3の数字を見比べると、その中で(1 2 3)と3個の整数を得るインターポレーションが可能である。
(インターポレーションは内挿とも言い、例えば1から3まで5回インターポレーションを行うと(1 1.5 2 2.5 3)というリストが得られる。これは和音の推移などにも応用できるが、今回はリズムに応用させる。)
例えば上の例だと、最初の(4 4)は4分の4拍子を指しているので無視し、1と3の数字を見比べると、その中で(1 2 3)と3個の整数を得るインターポレーションが可能である。
マルトの論文では、それらのインターポレーションを「ランダムに行う」と書いてあるので、まずはそのランダムのパッチを作ってみることとする。
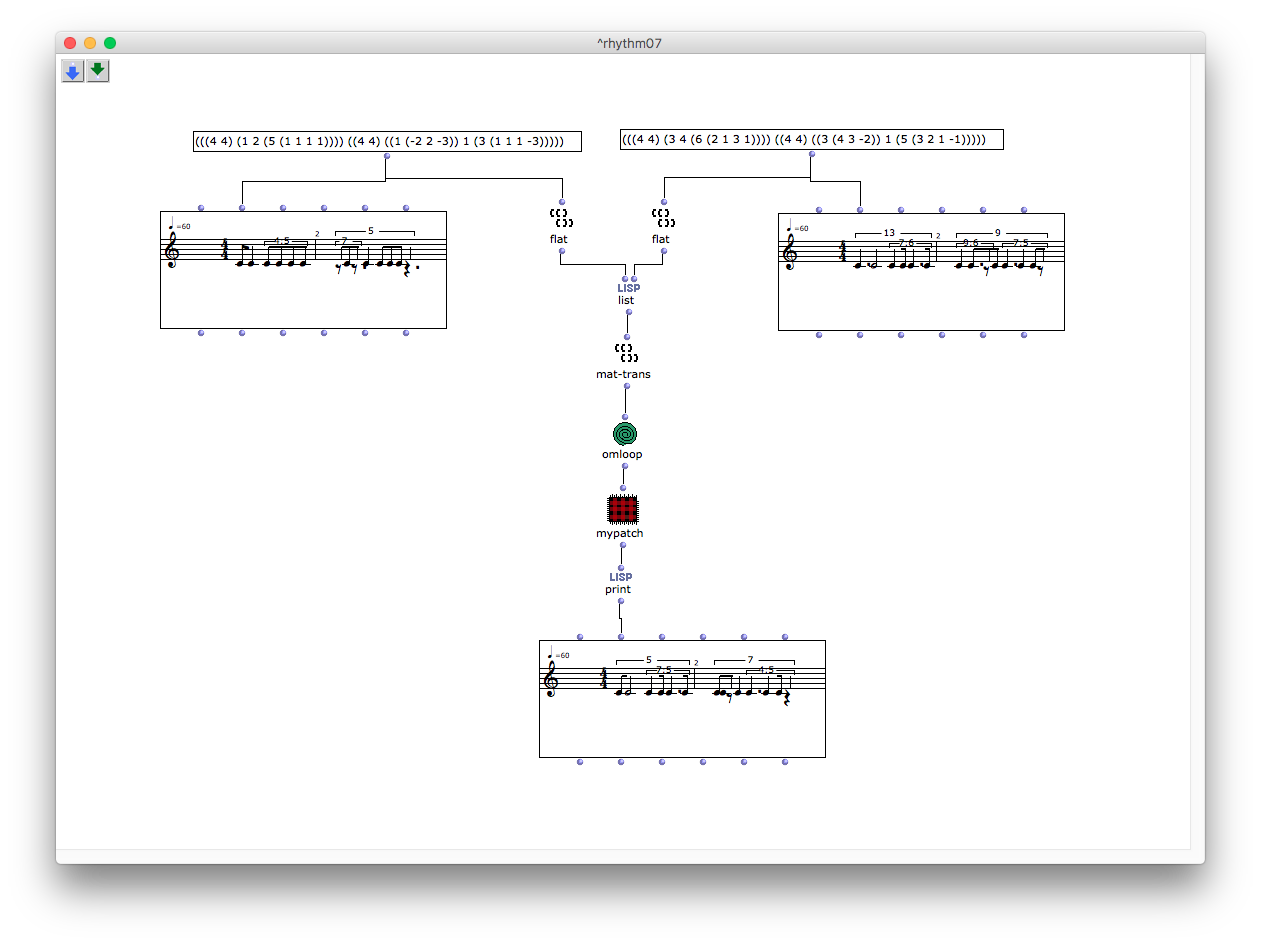
二つのリストを見比べるので、まずはそれぞれのリストから括弧をflatで全部取り去る。それをmat-transにかければ、それぞれの数字の2つのペアのリストが得られる。
(例えば((1 2 3 4 5) (6 7 8 9 10))をmat-transにかけると、((1 6) (2 7) (3 8) (4 9) (5 10))というリストが得られる。)
したがってここでの出力は、
((4 4) (4 4) (1 3) (2 4) (5 6) (1 2) (1 1) (1 3) (1 1) (4 4) (4 4) (1 3) (-2 4) (2 3) (-3 -2) (1 1) (3 5) (1 3) (1 2) (1 1) (-3 -1))
となる。
(例えば((1 2 3 4 5) (6 7 8 9 10))をmat-transにかけると、((1 6) (2 7) (3 8) (4 9) (5 10))というリストが得られる。)
したがってここでの出力は、
((4 4) (4 4) (1 3) (2 4) (5 6) (1 2) (1 1) (1 3) (1 1) (4 4) (4 4) (1 3) (-2 4) (2 3) (-3 -2) (1 1) (3 5) (1 3) (1 2) (1 1) (-3 -1))
となる。
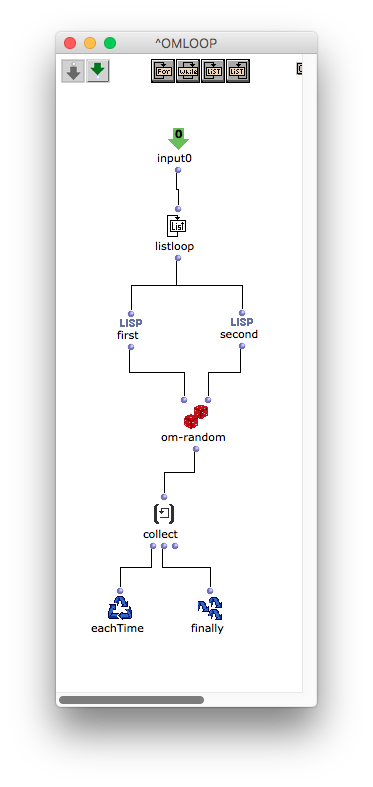
次はomloopの中を見てみよう。これはいたって単純である。first, secondで1番目、2番目の数値を取り出し、om-randomに入れれば良い。ここでは4/4拍子を表す最初の(4 4)を外すことを考慮していないが、(4 4)をom-randomに入れても常に4が出てくるので、ここでは特に処理していない。
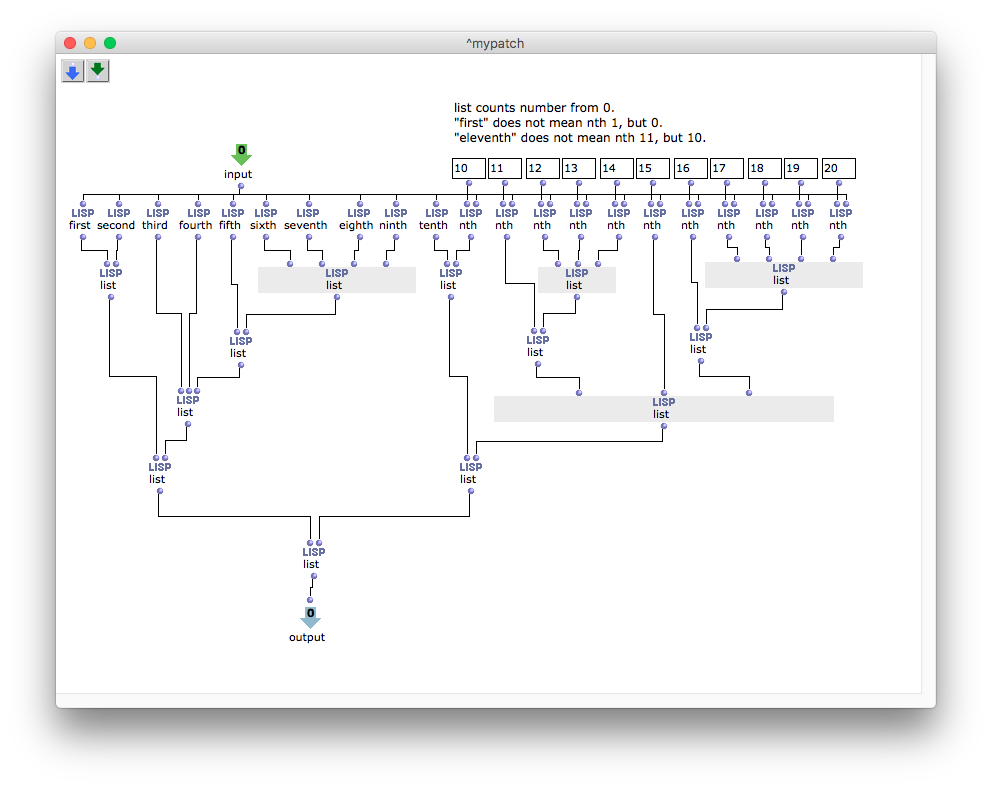
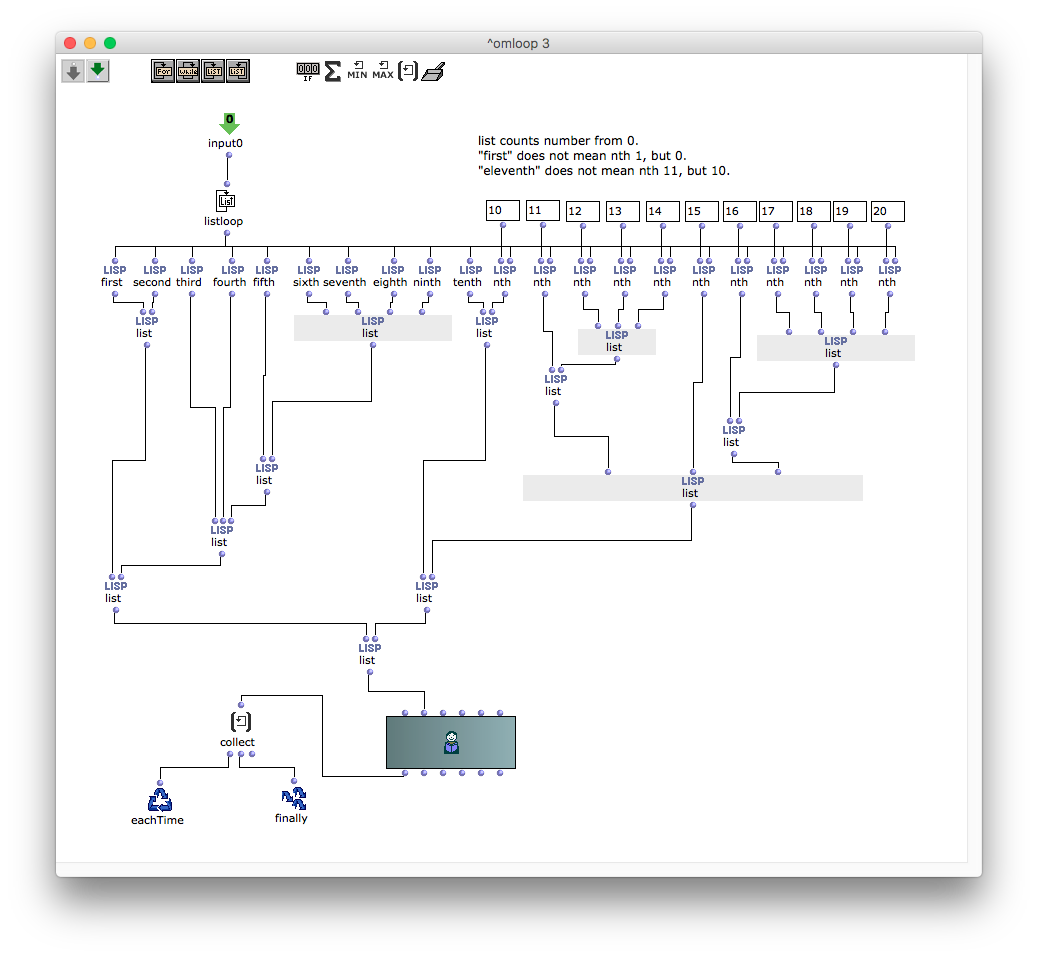
次はサブパッチでlistを組み合わせることによって括弧を再構成させている。(もう少しスマートな書き方があるはずだが、一応このように書いた。)
ここで注意するべき点は、first, second, ... tenthまではファンクションがあるが、eleventh以降は存在しないので、nthを使う必要がある。しかし、LISPは0からものを数えるので、 first の同義は nth 1 ではなく nth 0 である。 つまり eleventh の代用は nth 11 ではなく nth 10 にしなければならない。
最後のvoiceの結果は、ランダムによって、vキーでエヴァリュエートさせるたびに異なるリズムが出力させる。



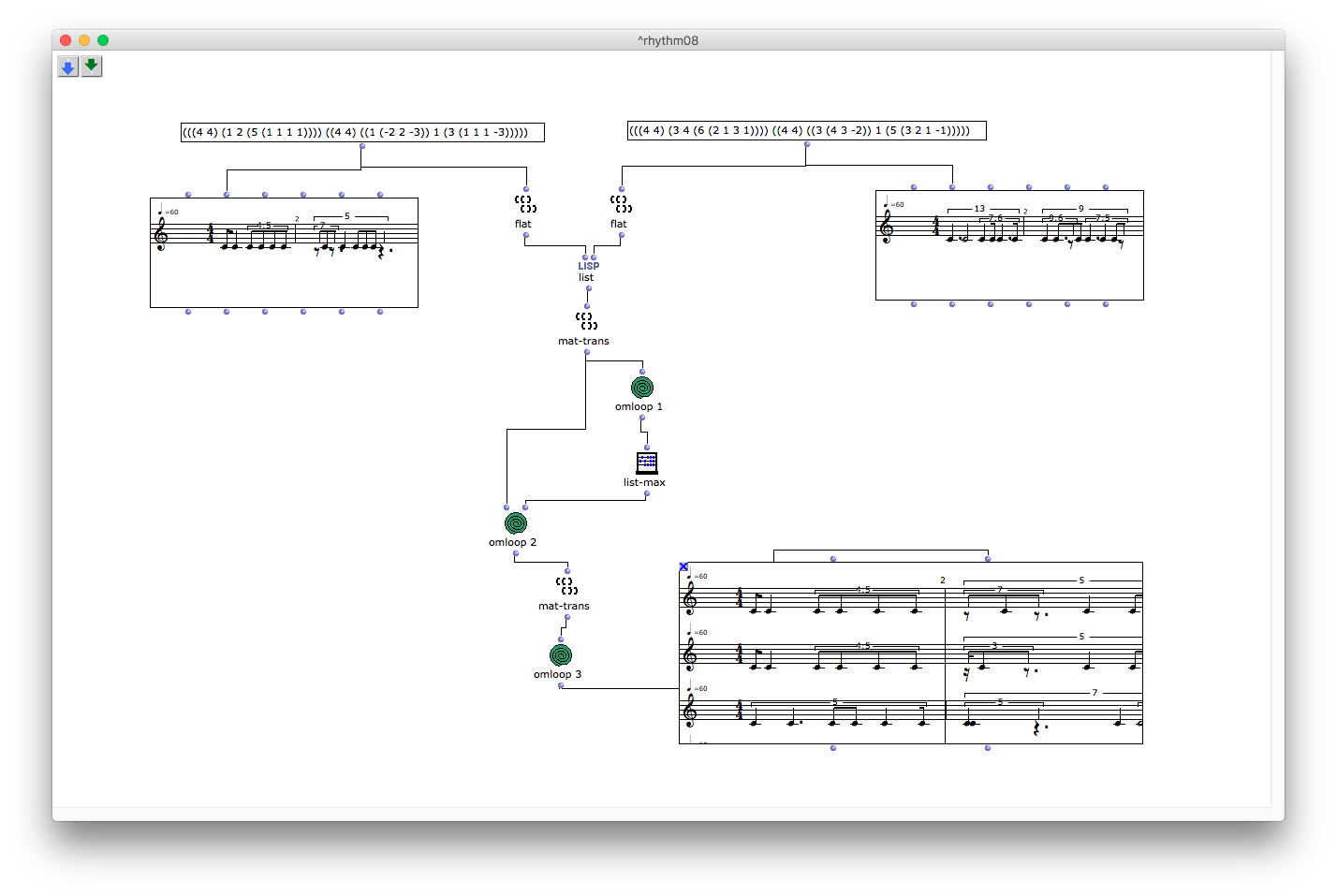
今度はこれをランダムではなく、リスト中の最大値でインターポレーションさせることによって全ての可能性を一覧のリストにするというように、パッチを改造してみる。(ここはマルトの論文では触れておらず、筆者imahoriが補完している)
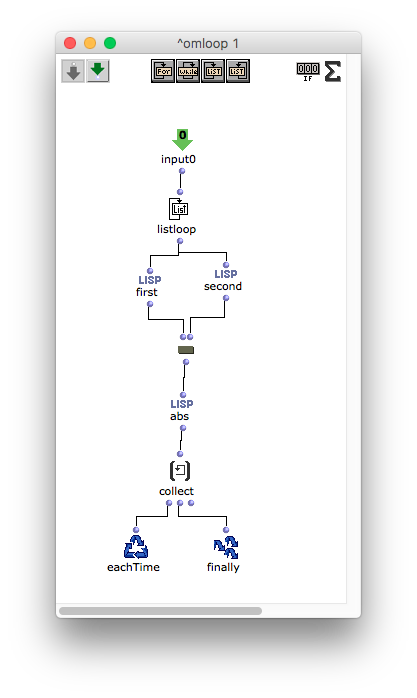
mat-transの部分までは先ほどのパッチと一緒である。今度はそれで得られた2つの数値を引き算し、absで絶対値(マイナスではない正の数にしたもの。3も-3も絶対値は3になる。)を求めた後、list-maxでそのリストの中の最大値を求める。今回は(-2 4)の6が最大値となる。
-2 - 4 = -6, abs 6
-2 - 4 = -6, abs 6
最大値での計算で整数を1ずつ得ようとすると、最初の数値から数えて (-2 -1 0 1 2 3 4) で7つの数値が必要になる。次のomloopでは、6に1を足して7でそれぞれの値をインターポレーションさせてみる。リズムツリーは小数点があるとタイを表すので、omーroundで小数点を切り捨てて整数で出力している。
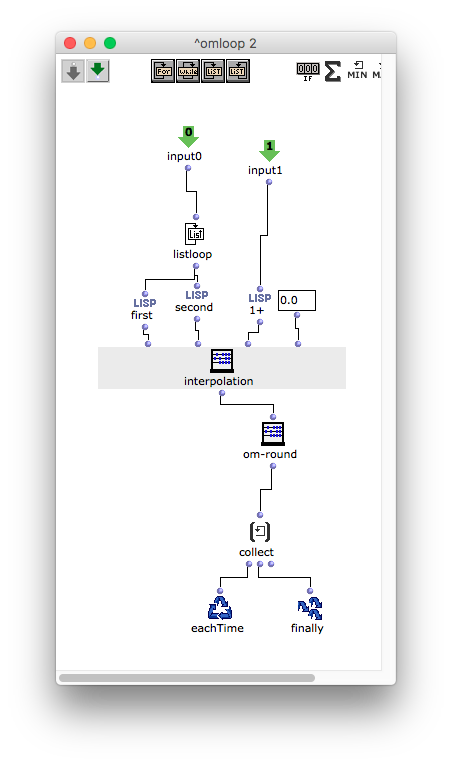
最後にそれをmat-transで整えたあと、先ほどのサブパッチと同じ要領でlistの組み合わせで括弧を再構成する。今回は複数のリストを扱うので、サブパッチの内容をomloopに移し替えれば良い。それをomloopの中でvoiceの第2インプットのリズムツリーに入力した後、voice全体をリストとしてomloopから出力させ、最後にpolyにまとめている。
結果は、以下のようなリズムのインターポレーションが得られる。
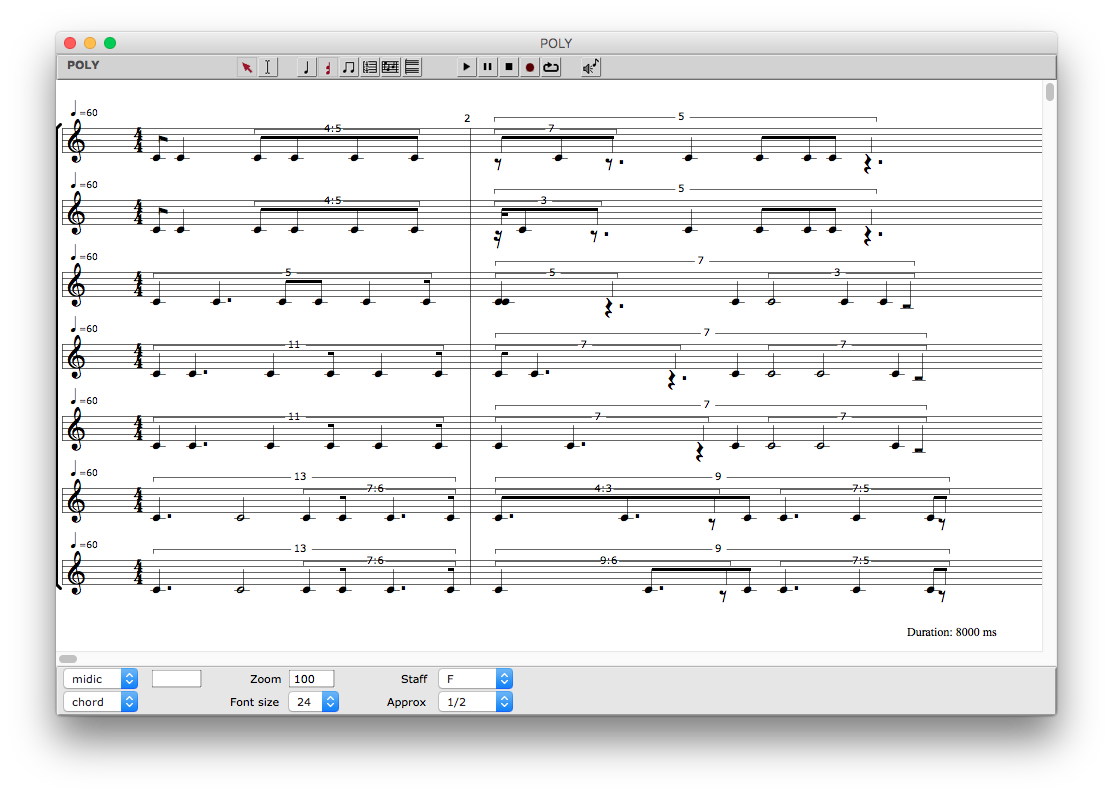
しかし、マルトの論文によると、ファーニホウ自身はこれを pre-compositional materials 作曲以前の素材 とし、直接は自身の作品には用いていない。
インターポレーションによるリストを用いてさらに応用させた例がマルトの論文の最後に紹介されているが、それはまた次回に書くこととする。
インターポレーションによるリストを用いてさらに応用させた例がマルトの論文の最後に紹介されているが、それはまた次回に書くこととする。
