非公式チュートリアル14 リズム2 ブライアン・ファーニホウのリズム分析と模倣1
現代音楽に携わる作曲家、演奏家、研究家の皆さんには周知のことと思うが、ブライアン・ファーニホウ Brian Ferneyhough という作曲家がいる。1943年イギリス生まれで、「新しい複雑性 new complexity」と呼ばれる作風を確立させた。
複層的に重なる非常に多くの連符を駆使した複雑なリズムを指定するのが、彼の楽譜の大きな特徴である。このスタイルは一時期1980-90年代に、ドイツのダルムシュタット夏季現代音楽講習会を中心に現代音楽界において大きな流行を築いた。彼の影響を受けた作曲家は数え切れないほど挙げられる。ファーニホウ自身、現在も健在で精力的に作曲活動を続けている。
楽譜著作権の問題を回避するために、他のブログ(おそらく公的な出版関連もの)から借用した楽譜を紹介する。
これは「土地 Terrain」(1992年)というヴァイオリンソロのための曲の冒頭部分である。
複層的に重なる非常に多くの連符を駆使した複雑なリズムを指定するのが、彼の楽譜の大きな特徴である。このスタイルは一時期1980-90年代に、ドイツのダルムシュタット夏季現代音楽講習会を中心に現代音楽界において大きな流行を築いた。彼の影響を受けた作曲家は数え切れないほど挙げられる。ファーニホウ自身、現在も健在で精力的に作曲活動を続けている。
楽譜著作権の問題を回避するために、他のブログ(おそらく公的な出版関連もの)から借用した楽譜を紹介する。
これは「土地 Terrain」(1992年)というヴァイオリンソロのための曲の冒頭部分である。
(掲載元ブログページ)
http://klangnewmusic.weebly.com/reverberations/brian-ferneyhoguh-collected-writings
(画像)
http://klangnewmusic.weebly.com/uploads/1/2/3/0/12308331/7797378_orig.jpg
http://klangnewmusic.weebly.com/reverberations/brian-ferneyhoguh-collected-writings
(画像)
http://klangnewmusic.weebly.com/uploads/1/2/3/0/12308331/7797378_orig.jpg
一見するとたじろいでしまうようなこれらの複雑なリズムは、実はある一定の規則性があって構築されている。しかもその規則性は、ある意味「拍子抜け」とも言うべき(!)ごく単純な数値の組み合わせ、たとえば (1 2 3 4 5 6) といった数値とそのヴァリエーションによって成り立っているのである。逆にいうと、そのような単純な数列からここまで複雑な楽譜を作るファーニホウの手腕は実に見事である。
今回はそれをOpenMusicによって再現する過程を解説する。
なおこの本文は、IRCAMの監修でedition Delatourから出版されたOM Composer’s Book 第2巻に掲載された、IRCAMの作曲家研究課程(cursus)の教授であるミハイル・マルト Mikhail Malt 氏による論文「ブライアン・ファーニホウの音楽言語におけるいくつかの考察」 Some considerations on Brian Ferneyhough's musical language を参照したものであることをお断りしておく。(しかし説明文をそのまま訳したのではなく、ある程度判りやすいように自分の言葉で書き換えており、パッチも必要に応じて改変している。)
This article is quoted the original examples from;
Mikhail Malt: Some considerations on Brian Ferneyhough's musical language
The OM composer's book. 2 (ed. Delatour, IRCAM), page 7-19
Mikhail Malt: Some considerations on Brian Ferneyhough's musical language
The OM composer's book. 2 (ed. Delatour, IRCAM), page 7-19

この例は(ミハイル・マルトの論文を参照した)、まず(5 4 3 6 2 1)という数列を用いてリズムパターンを作っている。折れ線グラフを表すクラスBPF (Break Point Filter)が間にわかりやすいように入っているが、これは別になくても良い。
pusemakerのinput 0と2に同じリスト(5 4 3 6 2 1)を入れ、input 0の拍子の分母は8を指定する。結果は、5/8, 4/8, 3/8, 6/8, 2/8, 1/8のそれぞれの拍子を持つ各小節ごとに8分音符の均等なリズムが並ぶ。

次の例は、pulsemakerのinput 2に、reverseでリストを反転させた(1 2 6 3 4 5)を入力した場合である。結果は、先ほどの拍子を持つ各小節に、それぞれ1 2 6 3 4 5 の数のアタックが入っている(1拍目はタイで2分音符と8分音符が繋がっているが、アタックは1つのみである)。

ここで、subst-rhythmというファンクションについて見てみよう。これはリズムツリーのある拍に対して、そこに下位のツリー構造を挿入するファンクションである。

例えば、(? (((4 4) (1 1 2))))というリズムツリーは、4分音符、4分音符、2分音符というリズムを持つ。これの最初の拍を(1 1)という2つの拍で分割する下位のツリーを挿入してみる。
subst-rhythmのinput 1(LISPは0からものを数えるので左から2つ目のインプット)にnilを指定すると、ファンクションは0が指定されたとして認識する。
結果は、1拍目の4分音符が2つに分割されるので、8分音符が2つ、4分音符、2分音符、というリズムに置き換えられる。
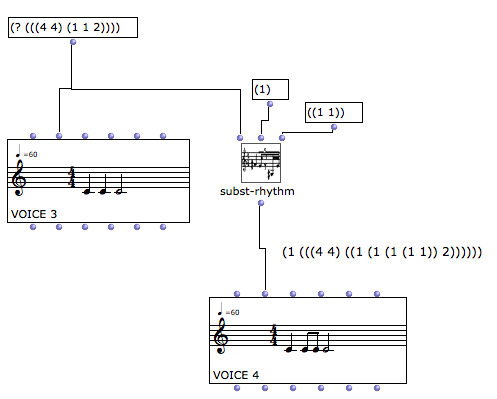
subst-rhythmのinput 1に(1)という1つの値だけを持つリストを指定してみる(値としての1では不可)。LISPは0からものを数えるので、1は2拍目を意味し、4分音符、8分音符が2つ、2分音符、というリズムになる。

先ほどのinput 1に(2)を指定すると、4分音符が4個並ぶ。これは元々の3拍目の2分音符が2つに分割されるので4分音符2つ分となり、結果として4分音符4つが並ぶのである。
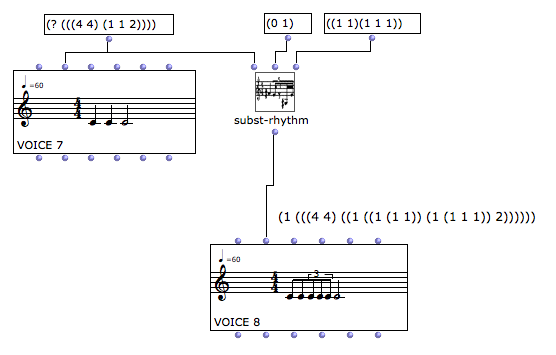
今度はinput 1に(0 1)リストを指定し、input 2には((1 1)(1 1 1))を指定してみる。結果は最初の1拍目の4分音符は(1 1)で2分割されて8分音符2個、次の2拍目の4分音符は(1 1 1)で3分割されて3連符8分音符が3個並ぶ。
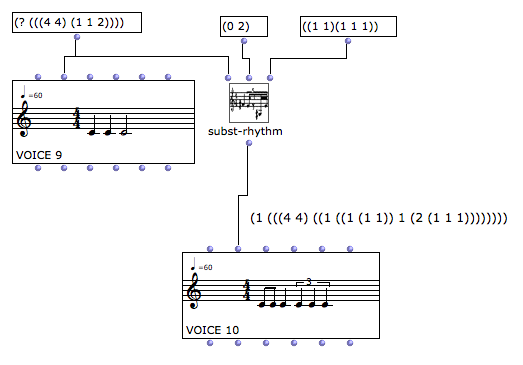
もしinput 1に(0 2)リストを指定すると、1拍目(0)と3拍目(2)が指定されることになる。結果は1拍目の4分音符は(1 1)で2分割されて8分音符2個、3拍目の2分音符は(1 1 1)で3分割されて3連符4分音符が3個並ぶ。

input 1に与えるリストの順を逆にして(2 0)と指定すると、3拍目の2分音符は(1 1)で2分割されて4分音符が2個並び、遡って1拍目の4分音符は(1 1 1)で3分割されて3連符8分音符が3個並ぶ。

再びミハイル・マルトの論文に戻る。この例では、先ほどの(5 4 3 6 2 1)で作られたリズムを、さらにsubst-rhythmで複層化したものである。
まず最初のリストから最後の値1を削除して(5 4 3 6 2)となったものを、dx->xで順に足したものが(0 5 9 12 18 20)となる。最初の0はcdrで消して(5 9 12 18 20)とする。また、それらに挿入される下位ツリー構造は、6は休符とし、(5 4 3 -6 2)と指定する。結果は、上記画像のようなリズムが得られる。
画像右側は、dx->xなどの計算過程を省略して直接パラメータをvoiceクラスに入力したものである。結果は同じリズムが得られる。
(2020.7.17追記)
詳しく見てみよう。まず我々は今、第1のリスト(5 9 12 18 20) と、第2のリスト(5 4 3 -6 2)という2つのリストを持っている。
上記画像の左上のvoiceの楽譜を見る。タイでつながった音符は1つと数えると、全部で21個のパルスがある。LISPは0からものを数えるので、最初の5/8の1小節目の2分音符とタイでつながった8分音符は0番目のパルスである。1番目(普通に1から数えると2番目)のパルスは、4/8の2小節目の最初の4分音符である。そうやって数えていくと、1つ目のリストの最初の数値である5にあたる、5番目(普通に1から数えると6番目)のパルスというのは、3/8の3小節目の16分音符の第3音ということになる。
ここで2つ目のリストの最初の数値を見るとやはり5であるが、この5は、その小節内の他のパルスに対して5倍の音価が入るということになる。つまり、左上のvoiceの楽譜では3/8の3小節目には16分音符が6つ入っているわけだが、これは(1 1 1 1 1 1)という「6つの1」が入っていたということになる。ところが今、これの第3音(3が指定してあるわけではなく、楽譜の先頭から数えて5、つまりLISPは0からものを数えるので普通に1から数えると6番目がたまたまこのリストの中の3番目にあたる)を、今度は第2のリストの最初の数値である5に置き換えようというわけだ。そうすると(1 1 5 1 1 1) というリストに置き換わる。ちなみに1+1+5+1+1+1=10である。
ところがその小節の3/8という拍は変わらないので、1という単位が狭くなって、本来16分音符6つぶんの均等パルス(32分音符だと12個入る)だったのが、今度はそれを10等分して、10:12(つまり5:6)の32分音符が1つの間隔になる。そこに1つずつのパルスと、3つ目は(10連32分音符で)5つ分(つまり4分音符とタイでつながった32分音符)の長さを持つ長いパルスが入ることになる。
想像してみよう。電車のドアとドアの間のロングシートの椅子に6人がけで座っていたとする。最初は均等な幅で座っていたのだが、ところが左から3番目の人が降りて、代わりにものすごーくデブな人が乗ってきて、5人分の横幅をその人が独占したとしよう。椅子の横幅(3/8)は変わらないから、仕方ないので左2人と右3人は、その5倍デブの人に圧迫されて、肩身狭く詰めて座らざるを得なくなる。
結果は左下のvoiceの3小節目のようになる。
次は、第1リストの2番目の数値である9ということで(0から数えて)9番目(普通に1から数えて10番目)のパルスを見てみよう。これは左上のvoiceで見ると、6/8の4小節目の第1音ということになる。第2リストの2番目の数値は4なので、今度はこの4小節目がもともと(1 1 1)で3分割されて4分音符3つ分だったのが、(4 1 1)となって4+1+1=6で6分割されることになる。そうすると1つのパルスはちょうど8分音符1個分ということになるが、4倍デブの人は2分音符、残り2人分のスペースを8分音符ずつで分け合う、ということになる。それが左下の4番目の小節、ということになる。
次は12番目のパルスである5小節目の最初の音が3倍デブ、パルス4つだったのが(3 1 1 1)で6つ分になる、ということで、理屈は先ほどと同じである。
最後の2つは少々ややこしい。なぜなら18番目のパルスも20番目のパルスも、同じ6小節目の中にあるからである。もともと5つのパルスがあって、1/8を5等分して5連32分音符5つ分の(1 1 1 1 1)だったこの小節は、数値が置き換わった結果 (1 1 -6 1 2) というものになっている。
6がマイナスなのは気まぐれだが、ともかくここは6倍の大デブと2倍のちょいデブがいて、残りの3人は肩身狭く詰めて座る、ということになる。
6を絶対値で正の数とみなすと、1+1+6+1+2=11である。そこでこの左下の1/8の6小節目は11等分されて、11連64分音符が1つずつのパルスとなり、3つ目の数値-6はマイナスがついているから休符となり、11連64分音符のパルス6つ分(つまり付点16分休符)となる。次はまた11連64分音符のパルス1つ分。最後は2なので、64分音符の2倍である32分音符となっている。
以上、ざっとであるが、左上voiceから左下voiceに至る楽譜の変化について解説した。ファーニホウ本人の複雑リズムを決定するプロセスの一端が垣間見えれば幸いである。
詳しく見てみよう。まず我々は今、第1のリスト(5 9 12 18 20) と、第2のリスト(5 4 3 -6 2)という2つのリストを持っている。
上記画像の左上のvoiceの楽譜を見る。タイでつながった音符は1つと数えると、全部で21個のパルスがある。LISPは0からものを数えるので、最初の5/8の1小節目の2分音符とタイでつながった8分音符は0番目のパルスである。1番目(普通に1から数えると2番目)のパルスは、4/8の2小節目の最初の4分音符である。そうやって数えていくと、1つ目のリストの最初の数値である5にあたる、5番目(普通に1から数えると6番目)のパルスというのは、3/8の3小節目の16分音符の第3音ということになる。
ここで2つ目のリストの最初の数値を見るとやはり5であるが、この5は、その小節内の他のパルスに対して5倍の音価が入るということになる。つまり、左上のvoiceの楽譜では3/8の3小節目には16分音符が6つ入っているわけだが、これは(1 1 1 1 1 1)という「6つの1」が入っていたということになる。ところが今、これの第3音(3が指定してあるわけではなく、楽譜の先頭から数えて5、つまりLISPは0からものを数えるので普通に1から数えると6番目がたまたまこのリストの中の3番目にあたる)を、今度は第2のリストの最初の数値である5に置き換えようというわけだ。そうすると(1 1 5 1 1 1) というリストに置き換わる。ちなみに1+1+5+1+1+1=10である。
ところがその小節の3/8という拍は変わらないので、1という単位が狭くなって、本来16分音符6つぶんの均等パルス(32分音符だと12個入る)だったのが、今度はそれを10等分して、10:12(つまり5:6)の32分音符が1つの間隔になる。そこに1つずつのパルスと、3つ目は(10連32分音符で)5つ分(つまり4分音符とタイでつながった32分音符)の長さを持つ長いパルスが入ることになる。
想像してみよう。電車のドアとドアの間のロングシートの椅子に6人がけで座っていたとする。最初は均等な幅で座っていたのだが、ところが左から3番目の人が降りて、代わりにものすごーくデブな人が乗ってきて、5人分の横幅をその人が独占したとしよう。椅子の横幅(3/8)は変わらないから、仕方ないので左2人と右3人は、その5倍デブの人に圧迫されて、肩身狭く詰めて座らざるを得なくなる。
結果は左下のvoiceの3小節目のようになる。
次は、第1リストの2番目の数値である9ということで(0から数えて)9番目(普通に1から数えて10番目)のパルスを見てみよう。これは左上のvoiceで見ると、6/8の4小節目の第1音ということになる。第2リストの2番目の数値は4なので、今度はこの4小節目がもともと(1 1 1)で3分割されて4分音符3つ分だったのが、(4 1 1)となって4+1+1=6で6分割されることになる。そうすると1つのパルスはちょうど8分音符1個分ということになるが、4倍デブの人は2分音符、残り2人分のスペースを8分音符ずつで分け合う、ということになる。それが左下の4番目の小節、ということになる。
次は12番目のパルスである5小節目の最初の音が3倍デブ、パルス4つだったのが(3 1 1 1)で6つ分になる、ということで、理屈は先ほどと同じである。
最後の2つは少々ややこしい。なぜなら18番目のパルスも20番目のパルスも、同じ6小節目の中にあるからである。もともと5つのパルスがあって、1/8を5等分して5連32分音符5つ分の(1 1 1 1 1)だったこの小節は、数値が置き換わった結果 (1 1 -6 1 2) というものになっている。
6がマイナスなのは気まぐれだが、ともかくここは6倍の大デブと2倍のちょいデブがいて、残りの3人は肩身狭く詰めて座る、ということになる。
6を絶対値で正の数とみなすと、1+1+6+1+2=11である。そこでこの左下の1/8の6小節目は11等分されて、11連64分音符が1つずつのパルスとなり、3つ目の数値-6はマイナスがついているから休符となり、11連64分音符のパルス6つ分(つまり付点16分休符)となる。次はまた11連64分音符のパルス1つ分。最後は2なので、64分音符の2倍である32分音符となっている。
以上、ざっとであるが、左上voiceから左下voiceに至る楽譜の変化について解説した。ファーニホウ本人の複雑リズムを決定するプロセスの一端が垣間見えれば幸いである。
(次回に続く)
