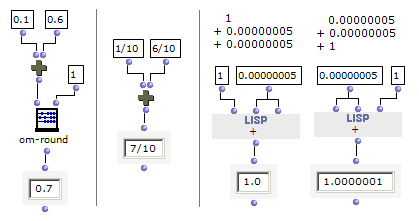
浮動小数点数型。いわゆる小数。
数値を、各桁の値の並びである「仮数部」と、小数点の位置を表わす「指数部」で表現する方法。
指数部によって小数点がふらふら動く。
数値を、各桁の値の並びである「仮数部」と、小数点の位置を表わす「指数部」で表現する方法。
指数部によって小数点がふらふら動く。

小数の型は主に2つ。デフォルトで使われる single-float型 と 倍精度 double-float型。
single-float型は、例えば単に「0.25」あるいは指数マーカーe・Eを使って「2.5e-1」など。
double-float型は、指数マーカーをd・Dにして例えば「2.5d-1」など。
single-float型は、例えば単に「0.25」あるいは指数マーカーe・Eを使って「2.5e-1」など。
double-float型は、指数マーカーをd・Dにして例えば「2.5d-1」など。
(他にもshort-float型やlong-float型があったり、single-float型の指数マーカーは実はf・Fだったりするのだが、わざわざ覚える程のものでもないかと。)
小数に誤差はつきもの
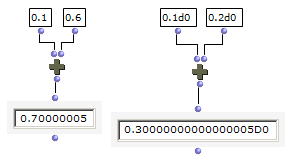
上図左のように、OMは「0.1 + 0.6」を「0.70000005」としてしまう(これはもちろん0.7と異なる数である)。なぜか。
OMに限らず、コンピュータ上ではほとんどの小数は近似値である。(*1)
例えば10進数の「0.1」は、コンピュータが扱う2進数の世界では「0.0001100110011・・・」のように「0011」の部分が繰り返し現れる循環小数、要するに割りきれない数である。コンピュータの桁数は有限なので適当な桁で丸めて扱う。single-floatでは「0.000110011001100110011001101」。
これは10進数に戻すと「0.100000001490116119384765625」であり、単に「0.1」と書かれた数は、実は内部では若干大きい数になっている。
小数が絡む演算を行うと、この誤差の影響が現れてしまう場合がある。
例えば10進数の「0.1」は、コンピュータが扱う2進数の世界では「0.0001100110011・・・」のように「0011」の部分が繰り返し現れる循環小数、要するに割りきれない数である。コンピュータの桁数は有限なので適当な桁で丸めて扱う。single-floatでは「0.000110011001100110011001101」。
これは10進数に戻すと「0.100000001490116119384765625」であり、単に「0.1」と書かれた数は、実は内部では若干大きい数になっている。
小数が絡む演算を行うと、この誤差の影響が現れてしまう場合がある。
これは倍精度のdouble-float型の場合でも同じことである(上例右)。確かに誤差は小さくなるんだけども。
対策
- 演算をできるかぎり整数型や分数型で行う。
- om-roundなどで適当な桁に丸める。(下例左。小数第1位より下の桁は必要ないので。)