関数の対称移動
関数の対称移動について扱います。
特に2次関数の対称移動について、平行移動と絡めた問題も扱います。
特に2次関数の対称移動について、平行移動と絡めた問題も扱います。
x軸対称
関数y=f(x)のグラフ上の任意の点をP(a,b)とする。
これをx軸に関して対称移動した点をQ(a,−b)とする。
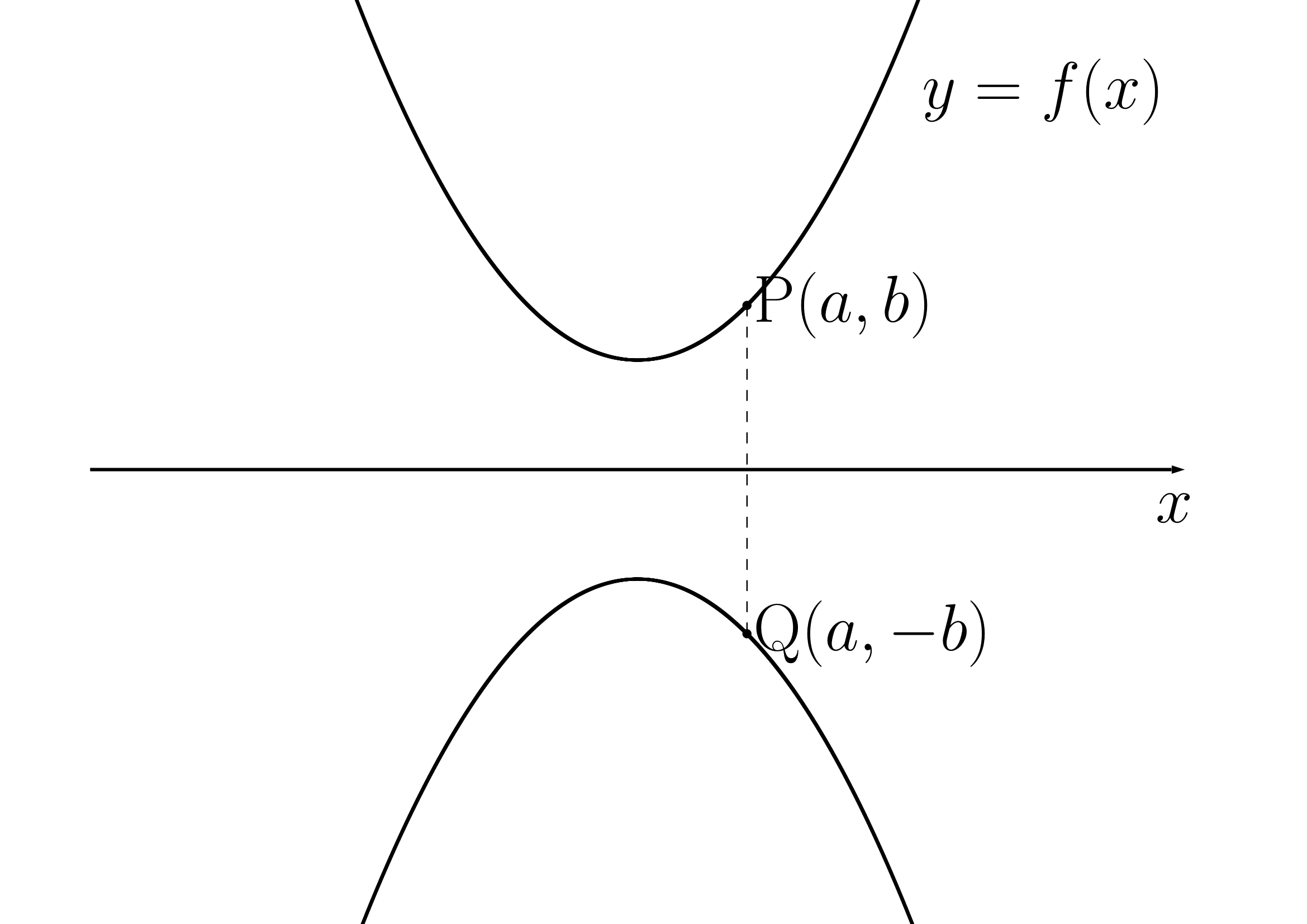
P(a,b)は関数y=f(x)上にあるから
これをx軸に関して対称移動した点をQ(a,−b)とする。
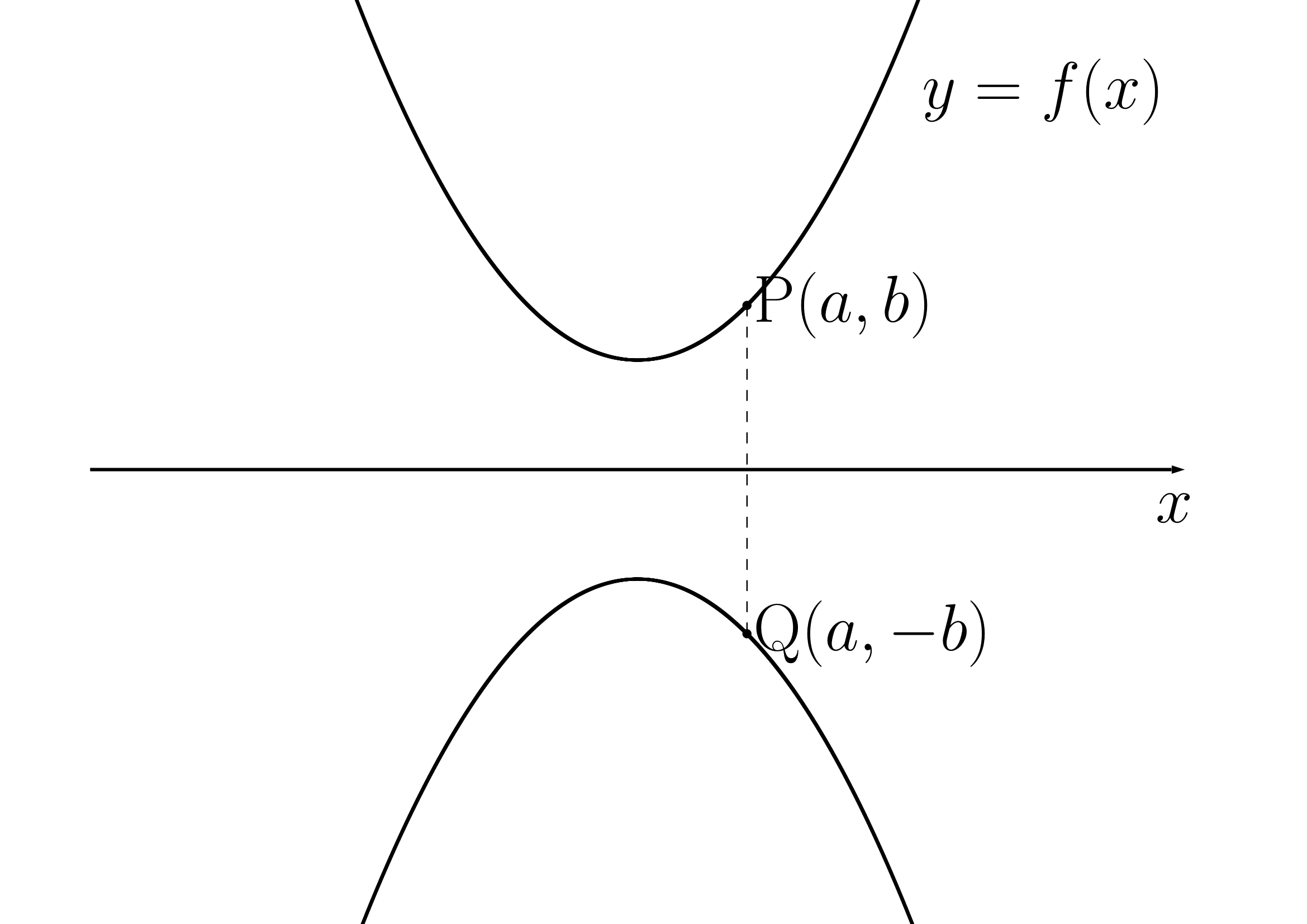
P(a,b)は関数y=f(x)上にあるから
b=f(a)
⇔-b=-f(a)
これはQが関数y=-f(x)上にあることを表している。
これより関数y=f(x)のグラフをx軸に関して対称移動したグラフを表す関数はy=−f(x)⟺−y=f(x)である。
これより関数y=f(x)のグラフをx軸に関して対称移動したグラフを表す関数はy=−f(x)⟺−y=f(x)である。
y軸対称
関数y=f(x)のグラフ上の任意の点をP(a,b)とする。
これをy軸に関して対称移動した点をQ(-a,b)とする。
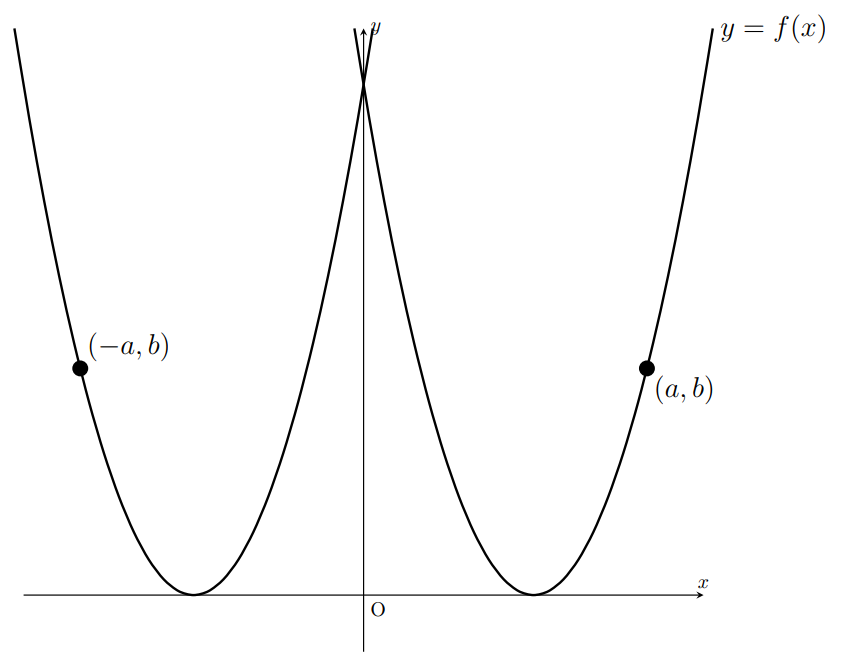
P(a,b)は関数y=f(x)上にあるから
これをy軸に関して対称移動した点をQ(-a,b)とする。

P(a,b)は関数y=f(x)上にあるから
b=f(a)
⇔b=f(-a)
これはQが関数y=f(-x)上にあることを表している。
これより関数y=f(x)のグラフをy軸に関して対称移動したグラフを表す関数はy=f(-x)である。
これより関数y=f(x)のグラフをy軸に関して対称移動したグラフを表す関数はy=f(-x)である。
原点対称
原点での点対称はx軸対称のグラフの、y軸対称のグラフである。
よってy=-f(-x)⇔-y=f(-x)である。
よってy=-f(-x)⇔-y=f(-x)である。
まとめ

関数y=f(x)のグラフをx軸,y軸,原点に関して対称移動したグラフはそれぞれ次のようになる。
- x軸:−y=f(x)
- y軸:y=f(−x)
- 原点:−y=f(−x)
※ 答える際はy=・・・の形で答えます.
問題
| + | ... |
| + | ... |
