(a+b)(c+d)=ac+ad+bc+bd
公式
数Iの展開公式を紹介します。
- 中学範囲
- 高校範囲
①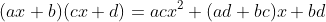
②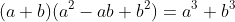
③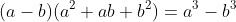
④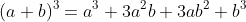
⑤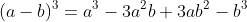
⑥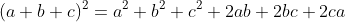
②
③
④
⑤
⑥
練習問題
次の式を展開せよ
(1)(3x-5y)2
(1)(3x-5y)2
| + | ... |
(2)(x+y-z)(x-y-z)
| + | ... |
(3)(x2+4x+8)(x2+4x-1)
| + | ... |
(4)(a-b+c)2-(a-b-c)2
| + | ... |
(5)(x+3)2(x-3)2
| + | ... |
(6)(x-2)(x+2)(x2+4)(x4+16)
| + | ... |
(7)(x-1)(x+2)(x-3)(x-6)
| + | ... |
(8)(4x+y)3
| + | ... |
(9)(4x-3y+5)2
| + | ... |
ac+ad+bc+bd=(a+b)(c+d)
公式
因数分解では基本的に展開の逆のことをします。
| + | 公式集 |
どんな問題もまずⅠ,Ⅱ,Ⅲを試みます。
- I共通因数があればくくる(全体ではなく個別にくくっても可)
- II公式が使えるか検討する(上の公式☆はたすきがけで対処)
- III同じ形を別の文字で置き換える。その後、因数分解の公式が使える形まで変形。
以上で最後まで解けない場合は下のいずれか、あるいは組み合わせて解きます。
- 文字が1種類のとき
複2次式(ax4+bx2+cの形)であれば強引に2乗の差を作る。
- 文字が2種類以上のとき
最低次数の文字について整理する。
たすきがけ
公式☆acx2+(ad+bc)x+bd=(ax+b)(cx+d)で、下の手順でa,b,c,dの値を見つける方法をたすきがけといいます。
a b →bc
×
c d →ad
ac bd (ad+bc)
- aとcを縦にかけてac
- bとdを縦にかけてbd
- aとd、bとcをそれぞれ斜めにかけてad,bc、足してad+bc
練習問題
面倒だった。誰か代わりにやってくれてもいいかもなぁなんて
