背理法 - 数学 @ ウィキ

という命題を示したいが直接示すのが困難な場合、と仮定して矛盾が言えれば、
が正しいと言える若干強引とも思える手法があります。
これを背理法といいます。

という命題を示したいが難しい

↓

と仮定して矛盾を言う

↓

が正しい

背理法は、世界が2分割(●か✖かのような)できる場合に強力ですがそうでない場合にはあまり有効ではありません。
例えば，実数の世界では必ず有理数と無理数に2分できますが、このような場合の証明に背理法は強力です。
「」の証明が難しいとき、「」の否定である「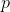かつ」として矛盾が言えればこれも背理法により「」が示せます．
対偶証明法と比較して示しやすい方を選択すればいいと思います．

問題

(1)素数が無限個存在することを示せ。

...

素数が有限個、すなわち個の素数が存在すると仮定する。
とすると、はのいずれでも割ることができないので素数となる。
これは個の素数が存在するとしたことに矛盾。
最初の仮定が誤りなので、素数は無限個存在する。
※文字をにしているのは素数(prime number)の頭文字に由来しています．

(2)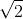は無理数であることを証明せよ。

...

が有理数であると仮定すると(，は互いに素な自然数)とおける。
ここから

は偶数なので、も偶数。
(は自然数)とおけるので

より
は偶数なので、も偶数。
以上より，はどちらも偶数なので，互いに素であることに反するので矛盾。
最初の仮定が誤りなので、√2が無理数である。
※2回も使用している、が偶数ならばは偶数であることの証明は付けなくていいことが多いです。
もし必要なら、命題の逆・裏・対偶の問題に同じ問題があります。
※やなどの場合も本質的に同じです。