2次関数のグラフの書き方 - 数学 @ ウィキ

2次関数

2次関数の導入をし、グラフの書き方を扱います。
2次関数は今後の数学の基礎になる分野で数学IAの中でも重要分野です。

軸と頂点

中学までは限定された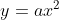までを考えていましたが，高校ではそれを平行移動させた一般の2次関数を扱います。
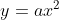をx軸方向にp,y軸方向にqだけ移動させた形で表せる関数を2次関数といいます。
この時関数は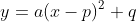で表され、これを基本形といいます。
また、これを展開し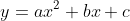で表したものは一般系といわれます。
※一般形や基本形という用語は正式な用語というより通称です。
一般形で出されたら平方完成という操作を行い基本形に変形することによってグラフを書くことができます。
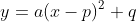においてのとき

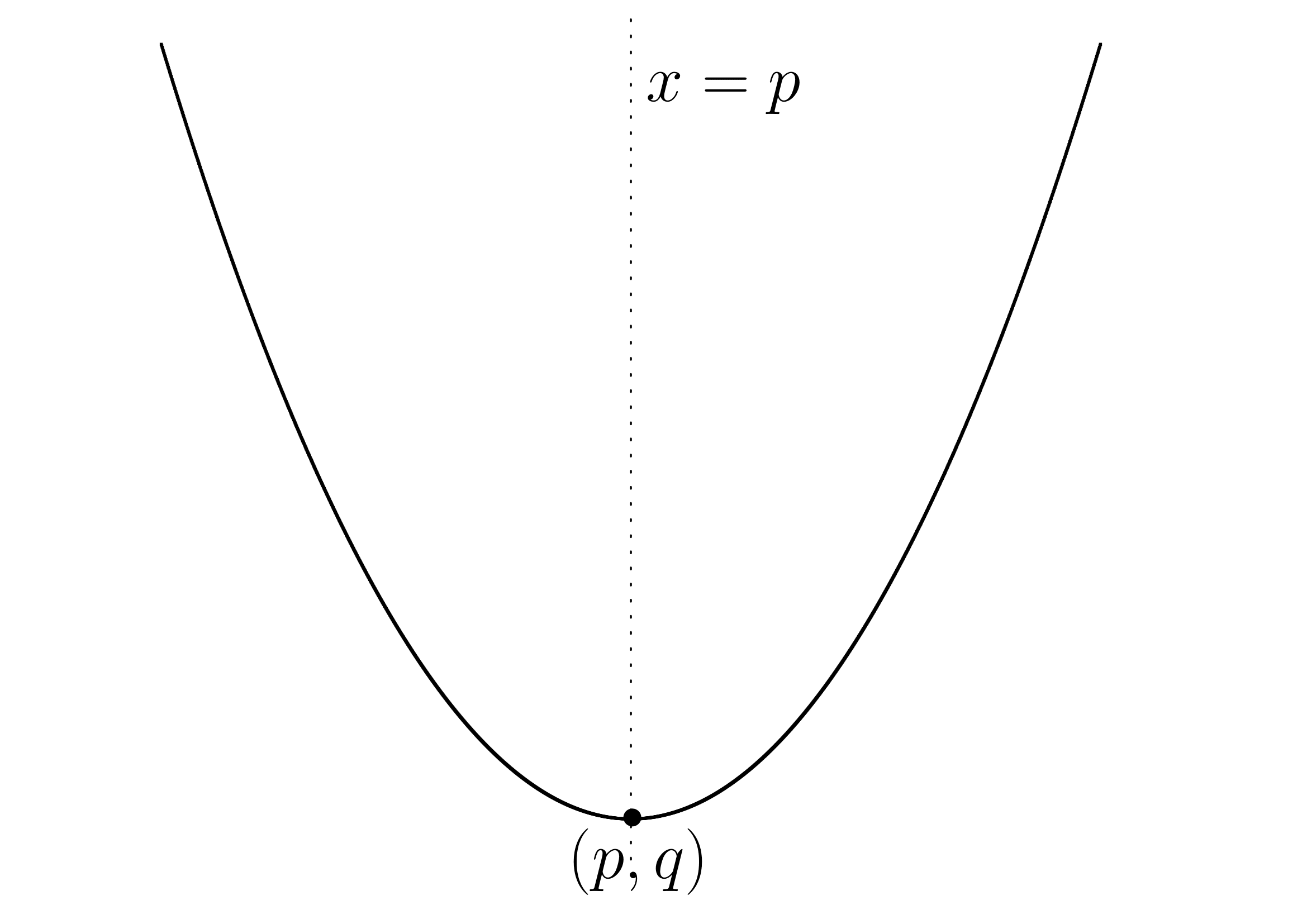
このようなグラフになります。
また、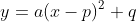においてのときは

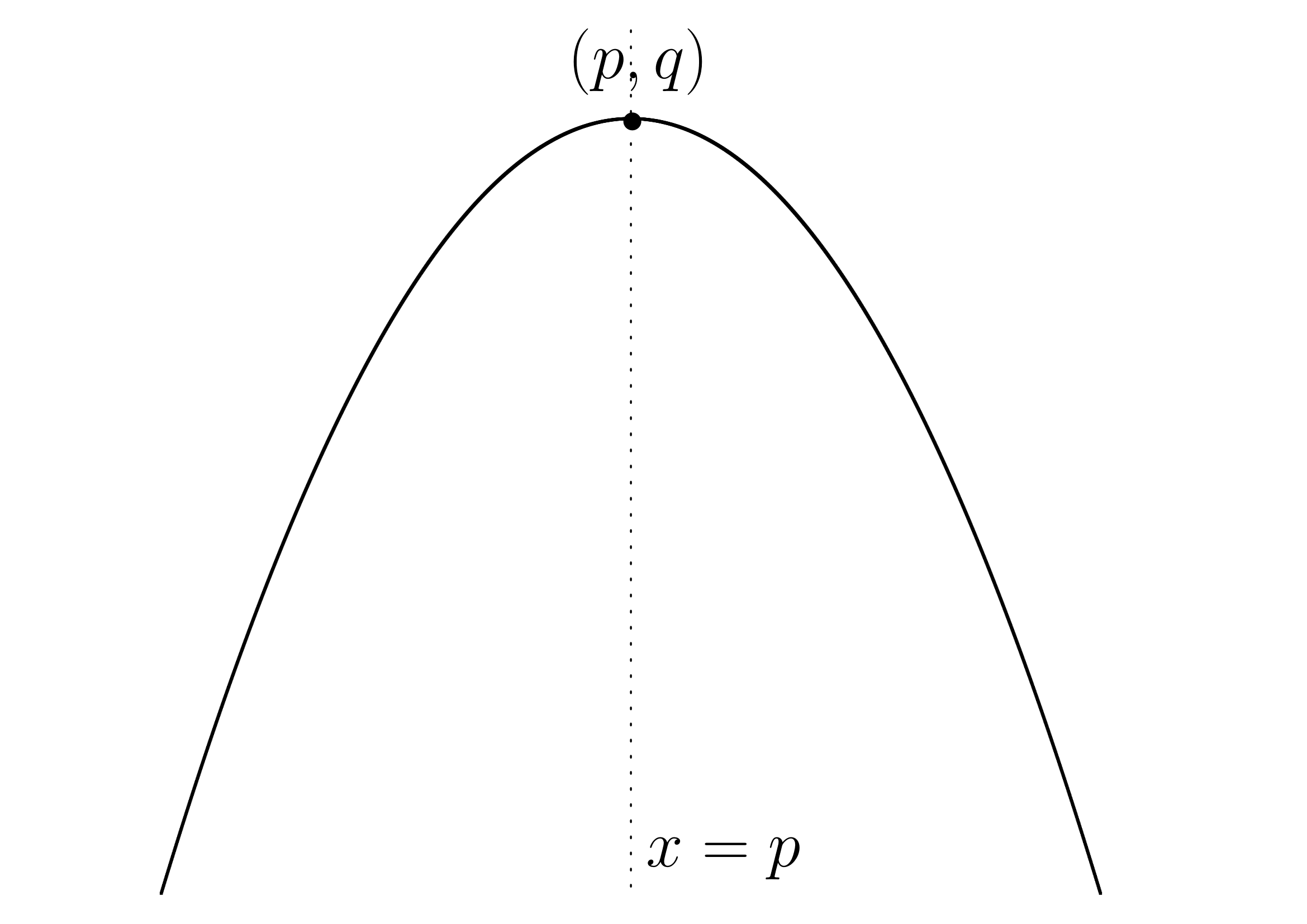
このようになります。
そしてこのという座標を頂点、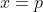となるところを軸といいます。

平方完成

軸と頂点(2次関数では頂点は軸を示す役割もあるため頂点のみでよい)を知るとグラフがかけるので、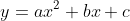を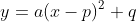に変形する方法を説明します。

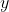
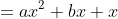
これより、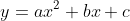において、軸は、頂点はであるとわかりました。

2次関数のグラフの基本的な書き方

沢山点の座標を書いていく必要はなく、頂点ともう1点うつと2次関数が決定するので、この論理でいうと最低この2点ほしいです。
2次関数のグラフの基本的な書き方

• のグラフを書きます。
• 平方完成して、頂点をうつ。
• 都合のいい点(y切片が楽です)をうつ。
• うった点を通るように、放物線を意識して書く。

※y切片とは点(0,c)のことです。
※頂点が無ければ3点必要ですが、普通頂点が必要でしょう。
このページではマス目など何もないところに書くことを前提としていますが、定期試験で解答欄にマス目がある場合は2次関数が通る格子点(xとy座標が整数な点)はすべて通さないと減点になる可能性があるので注意です。
以下で実際に問題を見て丁寧に解説します。

問題

次の2次関数の軸と頂点を求め、グラフをかけ。

...

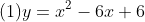
よって軸x=3，頂点(3,−3)
※の平方完成を使ってもよいし、この時軸は、頂点はになることをそのまま利用してもよい。
グラフ：

...

よって軸x=−1，頂点(−1,1)
グラフ:

...

よって軸x=2，頂点(2,2)
グラフ: