グラフの平行移動
グラフが形を保ったまま平面を移動する様子を見てみよう。
グラフの縦の移動
どんなグラフ でも、
でも、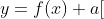 ただし
ただし と変形されると、グラフがaだけ上に移動する。
と変形されると、グラフがaだけ上に移動する。
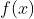 の値がaだけ足し算されているからだ。
の値がaだけ足し算されているからだ。
例:
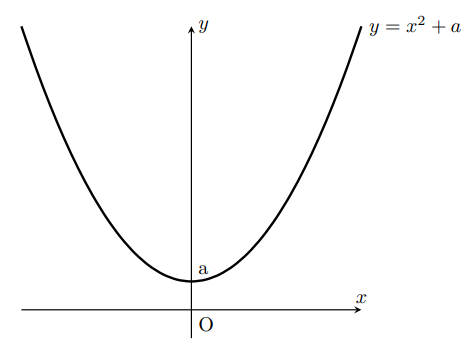
また、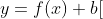 ただし
ただし についても同様にbだけグラフが下に下がる。
についても同様にbだけグラフが下に下がる。
例:
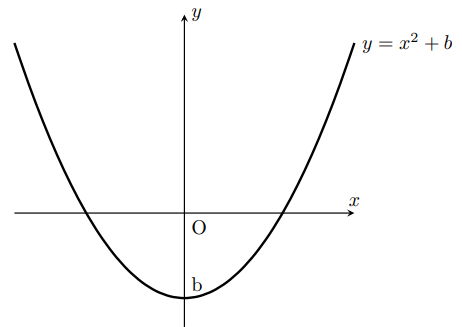
このように は、
は、 のグラフが、上下どちらかにqだけ移動するのだ。
のグラフが、上下どちらかにqだけ移動するのだ。
例:

また、
例:

このように
グラフの横の移動
ではグラフが横に移動する様子を確認してみよう。
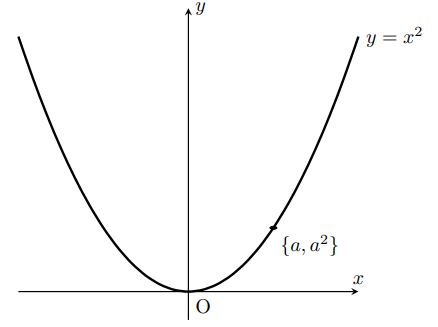
具体的に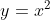 についてみてみる。
についてみてみる。
まず、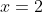 の時、
の時、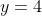 である。
である。
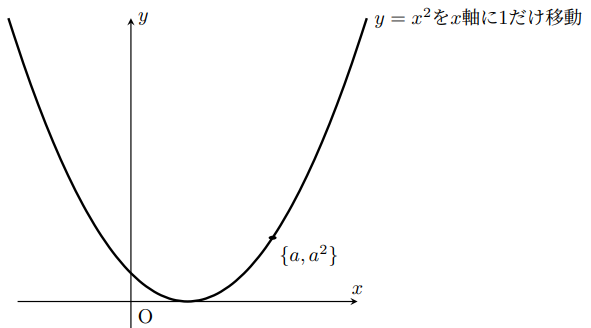
この時のグラフはこうである。
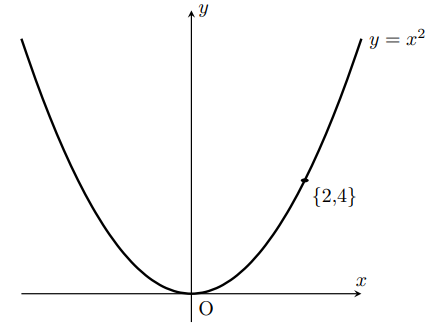
次にこのグラフを 方向だけ1動かし、
方向だけ1動かし、

上のようなグラフにしたいとしよう。
移動する前は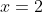 で
で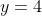 だったが、移動したため
だったが、移動したため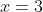 で
で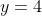 をとるようになった。
をとるようになった。
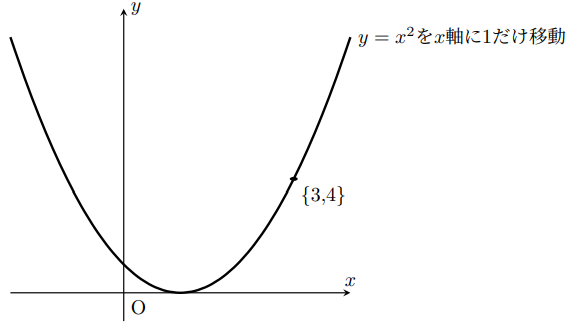
また、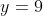 の時を考えよう。
の時を考えよう。
移動する前は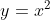 だから
だから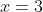 の時
の時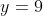 になる。
になる。
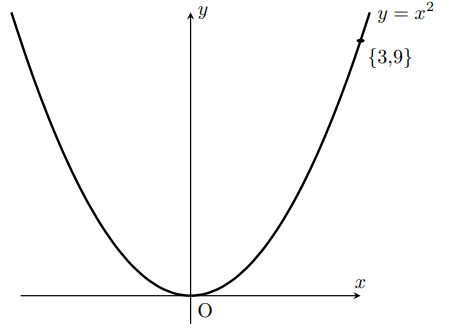
しかし移動した後は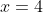 で
で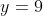 をとるようになった。
をとるようになった。
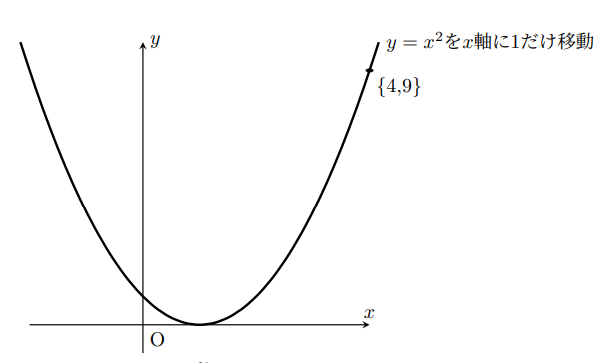
では定数 をつかって
をつかって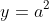 について調べよう。
について調べよう。
当然だが移動前は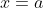 で
で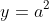 だ。
だ。
しかし移動した後は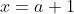 で
で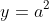 をとっている。
をとっている。
つまり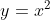 をx軸方向に1動かした関数は
をx軸方向に1動かした関数は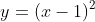 という関数になるのだ。
という関数になるのだ。
同様にx軸方向にp動かしたときは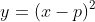 というグラフになる。
というグラフになる。
そしてさらには をx軸方向にp動かした関数は
をx軸方向にp動かした関数は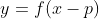 となる。
となる。
具体的に
まず、
この時のグラフはこうである。

次にこのグラフを

上のようなグラフにしたいとしよう。
移動する前は

また、
移動する前は

しかし移動した後は

では定数
当然だが移動前は

しかし移動した後は

つまり
同様にx軸方向にp動かしたときは
そしてさらには
