対称式
文字を入れ替えても変わらない多項式を対称式といいます。
例:



例:
基本対称式
基本的に、対称式の中でも以下を基本対称式といいます。
2つの変数の場合
3つの変数の場合
さらに多くの変数
上と同様に や
や なども基本対称式ですが、主に高校では大変なので2または3の変数のみを使ったものしか出てきません。
なども基本対称式ですが、主に高校では大変なので2または3の変数のみを使ったものしか出てきません。
そして、特筆すべきはすべての対称式は基本対称式のみで表現できることです。
ただしその証明はここでは省きます。
気になる人は数Bの内容なども含みますが、https://manabitimes.jp/math/1239なども見るとよいかもです。正直言って僕も証明はできません。
そして、特筆すべきはすべての対称式は基本対称式のみで表現できることです。
ただしその証明はここでは省きます。
気になる人は数Bの内容なども含みますが、https://manabitimes.jp/math/1239なども見るとよいかもです。
対称式を使った問題
以下の値を求めよ。
とする
(1)
(1)
| + | ... |
(2)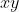
| + | ... |
(3)
| + | ... |
(4)
| + | ... |
次の値を求めよ
とする。
| + | ... |
| + | ... |
| + | ... |
x+y+z=4√3,xy+yz+zx=3,xyz=√2の時、次の式を求めよ
(1)x2+y2+z2
| + | ... |
(2)x2y2+y2z2+z2x2
| + | ... |
余談
対称式と非常によく似た、交代式というものがある。
交代式は、入れ替えても文字と符号しか入れ替わらない式のこと。
例えば、 や
や である。
である。
 と
と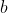 の交代式は、必ず
の交代式は、必ず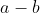 を因数に持ち、
を因数に持ち、
 と
と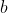 と
と の交代式は、必ず
の交代式は、必ず を因数に持つ。
を因数に持つ。
交代式は、入れ替えても文字と符号しか入れ替わらない式のこと。
例えば、
