ここでは中学校の範囲を学習済みであるとする。
目次
目次
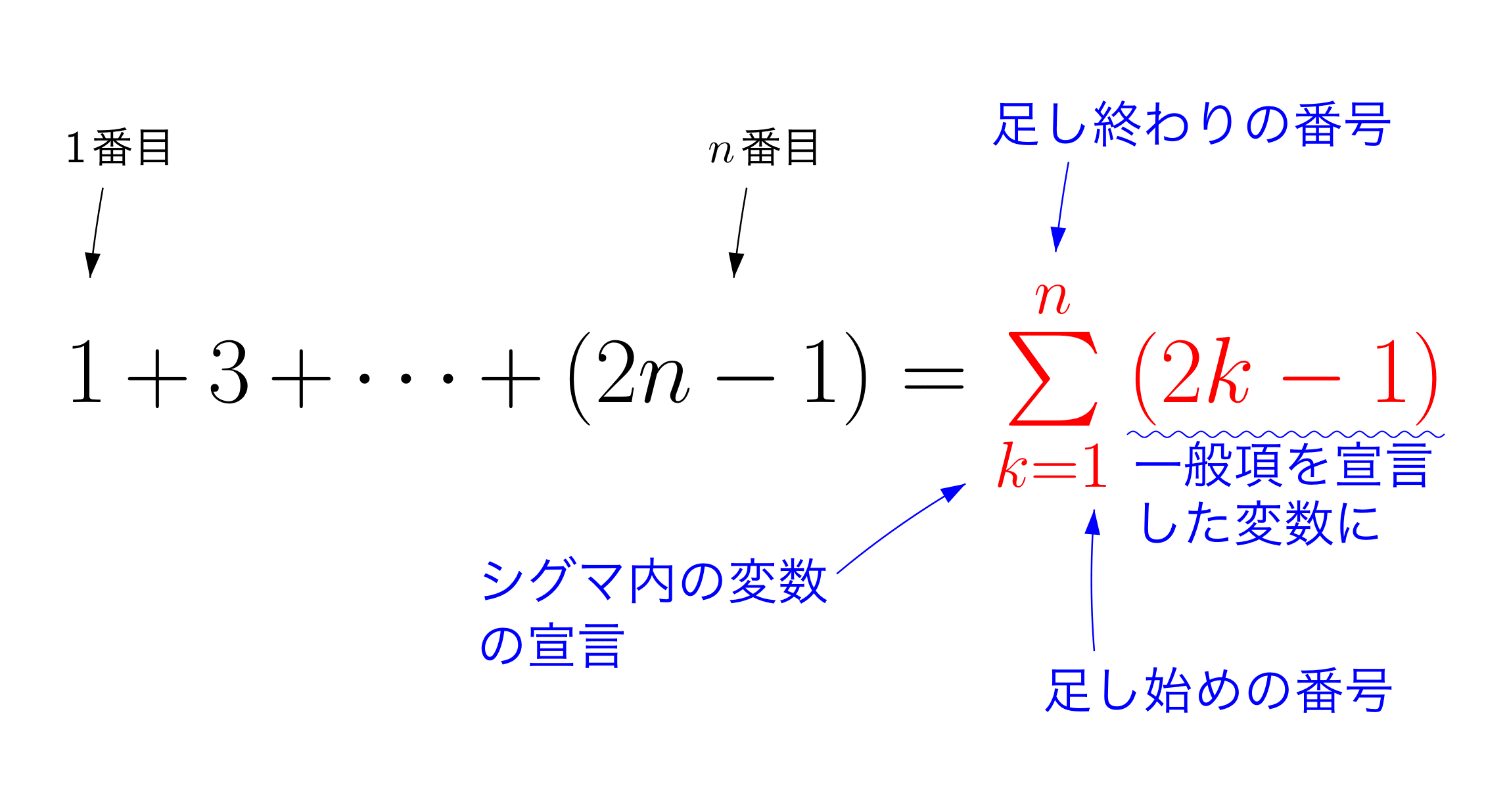
Σ
奇数列の1番目からn番目までの和を表現したいとき
1+3+5+⋯+(2n−1)
上のように書きますが、これは長ったらしいです。
そこで使われるのが、Σ記号です。
先ほどの式は
1+3+5+⋯+(2n−1)
上のように書きますが、これは長ったらしいです。
そこで使われるのが、Σ記号です。
先ほどの式は
と簡潔にあらわされます。
Σの下にk=1とありますが、これは「2k-1にまず最初にk=1を代入する。」ということを意味しています。
その上のnは、「2k-1にk=1から順番に自然数を代入するが、k=nを計算したら終わる。」
という意味を表しています。
また、奇数列や何かの数列を意味する記号としてanが使われます。
これは、例えば「素数のn番目をanと表す。」や、「√2の小数第n位の数をanとする。」のように使われます。
これを使うと、
Σの下にk=1とありますが、これは「2k-1にまず最初にk=1を代入する。」ということを意味しています。
その上のnは、「2k-1にk=1から順番に自然数を代入するが、k=nを計算したら終わる。」
という意味を表しています。

また、奇数列や何かの数列を意味する記号としてanが使われます。
これは、例えば「素数のn番目をanと表す。」や、「√2の小数第n位の数をanとする。」のように使われます。
これを使うと、
のような計算も可能になります。
場合の数
階乗
1からnまでの整数の積をn!と表します。つまり
例えば
順列
いくつかのものを一列に並べたものを順列といいます。
例として4人から2人選んで1列に並べる場合を考えます。
先頭に並ぶ人は4人のうちどれか一人なので4通りあり、その選び方それぞれに対して残りの3人の選び方の3通りあります。
これらは同時に起こらない(4人のABCDのうちAが先頭の時、BCDが同時に並んでABCのようになることはない)ので4×3=12通りあります。
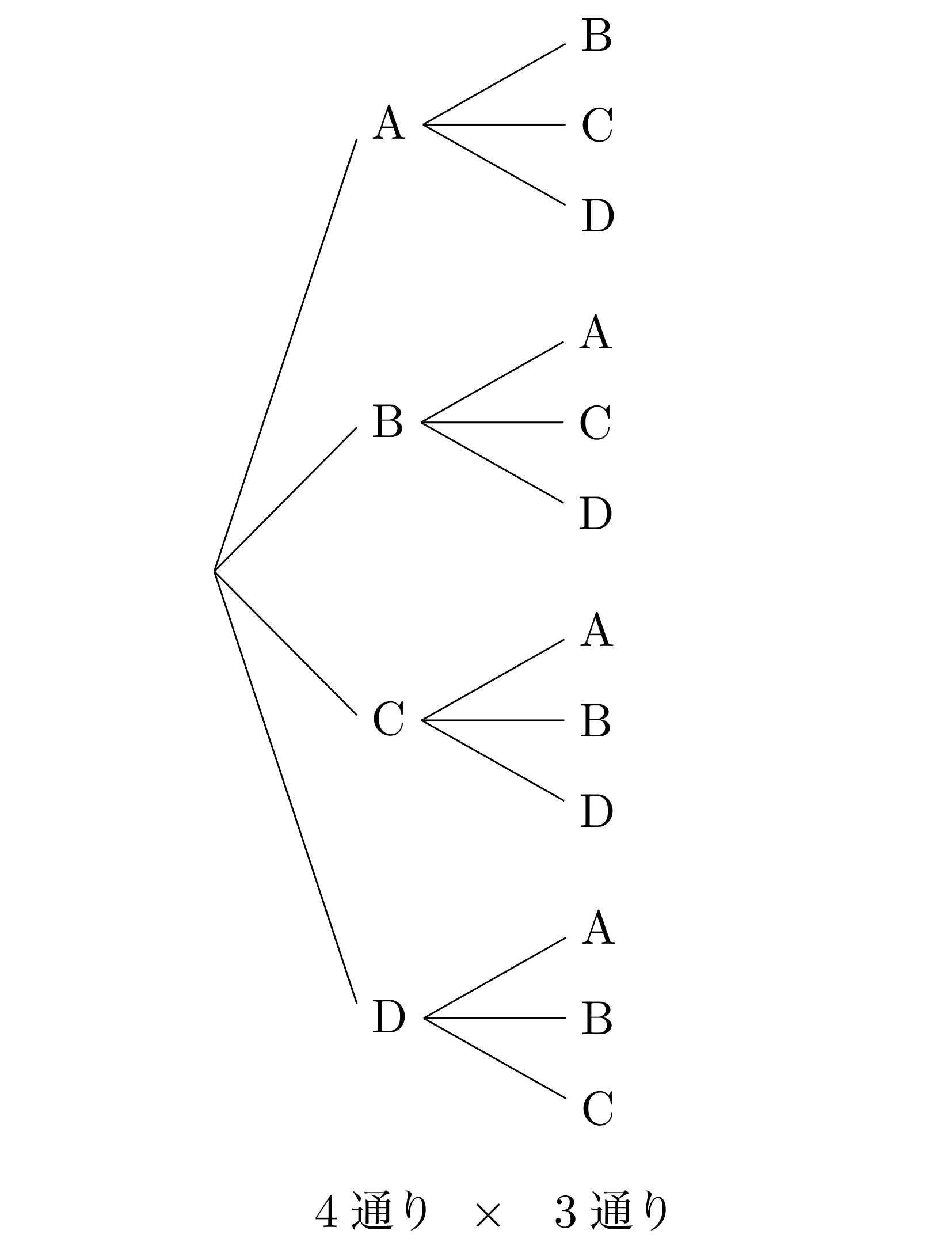
例として4人から2人選んで1列に並べる場合を考えます。
先頭に並ぶ人は4人のうちどれか一人なので4通りあり、その選び方それぞれに対して残りの3人の選び方の3通りあります。
これらは同時に起こらない(4人のABCDのうちAが先頭の時、BCDが同時に並んでABCのようになることはない)ので4×3=12通りあります。

先頭の決まり方 ×2番目の決まり方
同じように異なるn個からr個(1≦r≦n)とる順列の総数は
r個
※スマホのほうではうまく表示されないかもしれません
と表され、これを
と表され、これを
と定義します。
つまり、
つまり、
特に
つまり
はnから数字を下げていってr個整数をかけることで計算できます。
また、
また、
つまり、
順列の階乗表現で仮にr=nとすると
となるので、0!=1とするとr=nにも適用できます。
また先ほど述べたように、
また先ほど述べたように、
であり、つまり
ですが、
であるため、0!=1と定義します。
また、r=0とすると
また、r=0とすると
となるため
です。
組み合わせ
A,B,C,D,Eの5人から3人選ぶ選び方は何通りあるだろうか?
まず、選び方がx通りあるとします。
例えばA,B,Dが選ばれたとし、それを1列に並べると順列になり、その並べ方は3!通りです。
他のx通りの選び方に対しても3!通りあり、その合計は5P3通りになるので、
まず、選び方がx通りあるとします。
例えばA,B,Dが選ばれたとし、それを1列に並べると順列になり、その並べ方は3!通りです。
他のx通りの選び方に対しても3!通りあり、その合計は5P3通りになるので、
となります。
つまり
つまり
より10通りだとわかります。
同様に異なるn個からr個とる組合せの総数をxとすると、ある選び方に対しr!通りの並べ方があるので、
同様に異なるn個からr個とる組合せの総数をxとすると、ある選び方に対しr!通りの並べ方があるので、
つまり
です。
また、この時xを
また、この時xを
で表します。
よって
よって
特にnC1=n,nCn=1
また、
また、
を使うと
また、
二項定理
(a+b)4を展開公式を使わずに展開すると
(a+b)4
=(a+b)(a+b)(a+b)(a+b)
=(aa+ab+ba+bb)(a+b)(a+b)
=(aaa+aab+aba+abb+baa+bab+bba+bbb)(a+b)
=aaaa+aaab+aaba+aabb
+abaa+abab+abba+abbb
+baaa+baab+baba+babb
+bbaa+bbab+bbba+bbbb
上の式で,例えばa2b2では、
aabb,abab,abba,baab,baba,bbaa
の6つありますが、これはaとbが入るスペース4つのうち2個選んでaとし、残り2個をbとする組み合わせと同じだとわかります。
つまり数式にすると
(a+b)4
=(a+b)(a+b)(a+b)(a+b)
=(aa+ab+ba+bb)(a+b)(a+b)
=(aaa+aab+aba+abb+baa+bab+bba+bbb)(a+b)
=aaaa+aaab+aaba+aabb
+abaa+abab+abba+abbb
+baaa+baab+baba+babb
+bbaa+bbab+bbba+bbbb
上の式で,例えばa2b2では、
aabb,abab,abba,baab,baba,bbaa
の6つありますが、これはaとbが入るスペース4つのうち2個選んでaとし、残り2個をbとする組み合わせと同じだとわかります。
つまり数式にすると
のようになります。
同様に考えると、(a+b)4の展開は以下のように書けます。
同様に考えると、(a+b)4の展開は以下のように書けます。
つまり、一般に
ネイピア数(オイラー数)
単利と複利
単利と複利を説明する。銀行などではお金を預けると、利子が返ってくるが単利と複利ではその利子の付き方が変わります。
- 単利の場合
例えば、
10万円を年10%で貸した場合
1年後 → 10万円+1万円(利息)=11万円
2年後 → 11万円+1万円=12万円
3年後 → 12万円+1万円=13万円
というように単利では利息は元の10万円にだけつくので、毎年増えるお金の量は同じです。
10万円を年10%で貸した場合
1年後 → 10万円+1万円(利息)=11万円
2年後 → 11万円+1万円=12万円
3年後 → 12万円+1万円=13万円
というように単利では利息は元の10万円にだけつくので、毎年増えるお金の量は同じです。
- 複利の場合
例えば、
1年後 → 10万円+1万円=11万円
2年後 → 11万円+1.1万円(10%)=12.1万円
3年後 → 12.1万円+1.21万円=13.31万円
というように利息を合わせた去年の金額の合計に利息がつく。例のように10万円を年利10%で預けている場合、1年後も2年後も[元金(最初に預けた金額)+これまでの利息]に利子がかかります。
例の場合を詳しくいうと、
1お金を預けた時
一年後には元の1+利子の0.1=1.1
2年後には1.1+1.1・0.1=1.1(1+0.1)=1.1・1.1=1.12
3年後には1.12+1.12・0.1=1.12(1+0.1)=1.12・1.1=1.13
・・・n年後には1.1nとなります。
1年後 → 10万円+1万円=11万円
2年後 → 11万円+1.1万円(10%)=12.1万円
3年後 → 12.1万円+1.21万円=13.31万円
というように利息を合わせた去年の金額の合計に利息がつく。例のように10万円を年利10%で預けている場合、1年後も2年後も[元金(最初に預けた金額)+これまでの利息]に利子がかかります。
例の場合を詳しくいうと、
1お金を預けた時
一年後には元の1+利子の0.1=1.1
2年後には1.1+1.1・0.1=1.1(1+0.1)=1.1・1.1=1.12
3年後には1.12+1.12・0.1=1.12(1+0.1)=1.12・1.1=1.13
・・・n年後には1.1nとなります。
年利100%
次に年利100%の複利について考えます。
あたり前ですが年利100%では1お金を預けると一年後には
1+1・100%=1+1=2
です。
ではこれを半年に50%ずつ増える、一年で合計100%になる場合を考えます。
一見すると、これは先ほどと何も変わっていないように思われますが、
半年で1+0.5(50%)=1.5
1年で1.5+1.5・0.5=1.5(1+0.5)=1.5・1.5=1.5^2=2.25
となります。
同様に分割回数を増やしてみます。
3分割:
あたり前ですが年利100%では1お金を預けると一年後には
1+1・100%=1+1=2
です。
ではこれを半年に50%ずつ増える、一年で合計100%になる場合を考えます。
一見すると、これは先ほどと何も変わっていないように思われますが、
半年で1+0.5(50%)=1.5
1年で1.5+1.5・0.5=1.5(1+0.5)=1.5・1.5=1.5^2=2.25
となります。
同様に分割回数を増やしてみます。
3分割:
※≈とは≒(ニアイコール)とおなじく「大体等しい。」「このくらい。」という意味があります。
4分割:
4分割:
もうお気づきの方もおられるかもしれませんが、n分割したときの式は
になります。
ではこの公式を使って、さらに分割しましょう。
5分割:
ではこの公式を使って、さらに分割しましょう。
5分割:
6分割:
10分割:
一見すると増加しているように見えます。
しかし、分割回数を極端に大きくしてみると、
100分割:
しかし、分割回数を極端に大きくしてみると、
100分割:
200分割:
1000分割:
だんだんと 2.71・・・ に収束しているように見えます。
実際これは正しくて、グラフを書くとある値に収束していくのがわかります。
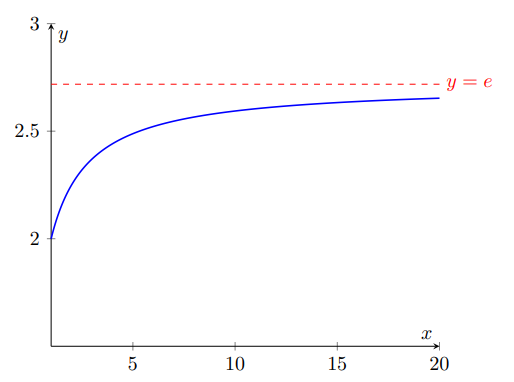
この収束する値こそが e ことオイラー数(ネイピア数とも言う)なのです。
これを数式に書くとき
実際これは正しくて、グラフを書くとある値に収束していくのがわかります。

この収束する値こそが e ことオイラー数(ネイピア数とも言う)なのです。
これを数式に書くとき
としてしまうと、数学において無限とはとてもあいまいな数字であり、例えば
です。
なので、先ほどの式だと
なので、先ほどの式だと
というあり得ない式が成立してしまいます。
そこで数学者はこのような誤解を防ぐために、「だんだん大きくする」ことで、「極限まで数を大きくしたとき」どのような値になるかを推測するという概念を作り出しました。
これこそが
そこで数学者はこのような誤解を防ぐために、「だんだん大きくする」ことで、「極限まで数を大きくしたとき」どのような値になるかを推測するという概念を作り出しました。
これこそが
の意味です。(※この場合、hを極限まで無限大に近づけていく、という意味です。)
これを使うと
これを使うと
となります。
三角関数
sinとcosの定義から話を進める。
まず、円の中心をOとし、半径が1の円上に点Pを取る。
そしたらx軸と線分OPの作る角をθと定義する。
その時の点Pの座標をP(cosθ,sinθ)とするのだ。
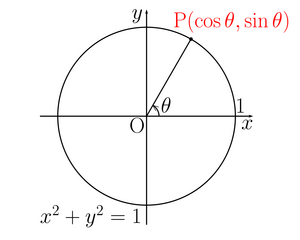
まず、円の中心をOとし、半径が1の円上に点Pを取る。
そしたらx軸と線分OPの作る角をθと定義する。
その時の点Pの座標をP(cosθ,sinθ)とするのだ。

は無視してください。)
つまり、
sinθ=Pのx座標
cosθ=Pのy座標
である。
この時、線分OPの傾きをtanθとするのだ。
ちなみにOPは、Oからx座標にcosθ,y座標にsinθ進んでいるので傾きは
つまり、
sinθ=Pのx座標
cosθ=Pのy座標
である。
この時、線分OPの傾きをtanθとするのだ。
ちなみにOPは、Oからx座標にcosθ,y座標にsinθ進んでいるので傾きは
と表せる。
よって
よって
であるとわかる。ただしθ=90°の時
となるためtan90°は定義不可能である。
また、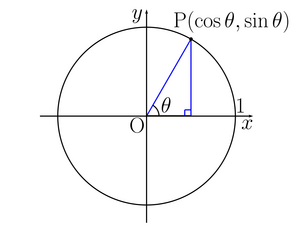
このように0≤θ<90°の時Pの座標をP(Px,Py)とすると、
また、

このように0≤θ<90°の時Pの座標をP(Px,Py)とすると、
であると定義できる。
また、
また、
であるとわかる。
つまり、
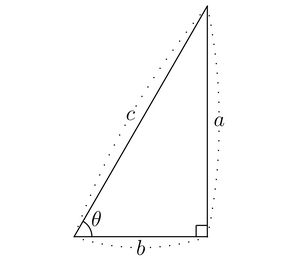
(ただし0°≤θ<90°)となる直角三角形ABCにおいて
つまり、

(ただし0°≤θ<90°)となる直角三角形ABCにおいて
という定義の仕方もできるのだ。
三角関数の相互関係

この図から三平方の定理を用いると、
であるとわかる。また、これをsin2θで割ると、
になる。
還元公式

上のような図では、y座標を線対称の軸として、線対称になっているのがわかる。
ここから、
であるとわかる。
しかし、同時に
しかし、同時に
でもあるので
であるとわかるのだ。
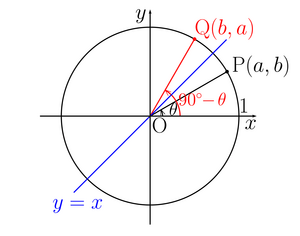
(y=xは無視してください。)
上の図から、Qについてみると

(y=xは無視してください。)
上の図から、Qについてみると
だとわかる。
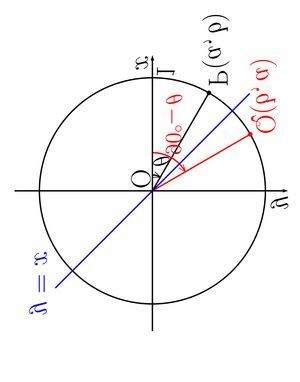
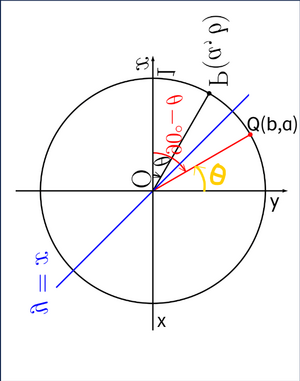
また、このようにグラフを回転させてみると、回転されているためxとy座標の位置関係が普通のグラフと逆であり、Qについて


また、このようにグラフを回転させてみると、回転されているためxとy座標の位置関係が普通のグラフと逆であり、Qについて
であるとわかる。つまり、
である。
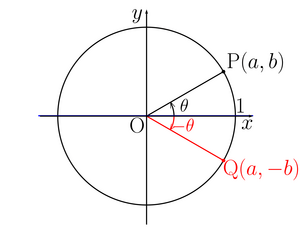
上の図から

上の図から
とすると、
という風に反転していることがわかる。また、同時に
であるともわかる。つまり
である。
弧度法

Oを中心として回転する半直線OPを動径といい、位置がOXの時、半直線OXを始線といいます。
反時計回りの回転を正の向き、時計回りの回転を負の向きといい、負の向き及び1回転以上の角度も含めたものを一般角といいます。
一般角では、複数の角度が対応します。

このように、上の図から60°と-300°は同じであることがわかります。
420°や-660°も同じであり、上の図の動径OPが表す角は、
ただし(nは自然数)
という風にまとめて表現できます。
今までの30°のような表し方を度数法といいます。
角度にはこのほかにラジアンという表し方があります。ラジアンさんはここから来たんですね。
ラジアンの定義はこうです。
という風にまとめて表現できます。
今までの30°のような表し方を度数法といいます。
角度にはこのほかにラジアンという表し方があります。
ラジアンの定義はこうです。
半径が1の扇形の、孤の長さがθのときの中心角をθ[rad]と定義する。

※[rad]はラジアン[radian]という単位の省略形です。
例えば半径1で90°ならば、扇形の孤の長さは
なので、
であるとわかります。

同様に、以下のようになります

同様に、以下のようになります
| 度数法(°) | 30 | 45 | 60 | 90 | 180 | 360 |
| 弧度法([rad]) |
また、
より
です。
ちなみに一般角と同じく弧度法では負の角度や1回転以上の角度も適用します。
また、扇形の半径をr、中心角をa°としたとき面積は、
ちなみに一般角と同じく弧度法では負の角度や1回転以上の角度も適用します。
また、扇形の半径をr、中心角をa°としたとき面積は、
となりますが、弧度法を用いると、
であるため、中心角をx[rad]としたとき
と求められます。
同様に弧の長さも
同様に弧の長さも
となります。
加法定理
単位円周上にP(1,0),Q(cos(α+β),sin(α+β))をとる。
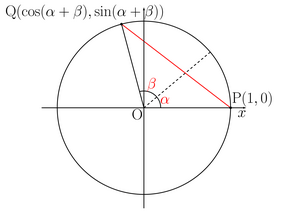
この時、PQ2は三平方の定理を用いて

この時、PQ2は三平方の定理を用いて
である。
このP,Qを原点を中心に−α回転した点をそれぞれP'(cos(−α),sin(−α)),Q'(cosβ,sinβ)とする。
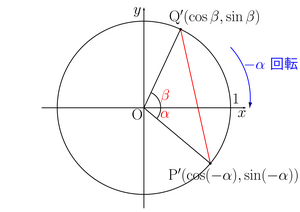
この時、先ほど同様にP'Q'2は三平方の定理を用いて
このP,Qを原点を中心に−α回転した点をそれぞれP'(cos(−α),sin(−α)),Q'(cosβ,sinβ)とする。

この時、先ほど同様にP'Q'2は三平方の定理を用いて
これは、PQを回転させただけなのでP'Q'=PQである。
つまりPQ2=P'Q'2である。よって
つまりPQ2=P'Q'2である。よって
である。
これのβに-βを代入すると、
さらにこの式のαにπ/2-α[rad]を代入すると
※π/2[rad]=90°で、どちらで計算してもよい
※π/2[rad]=90°で、どちらで計算してもよい
そしてβに-βを代入すると、
微分
まずは、どうすれば関数のグラフの接線を引けるのだろう?
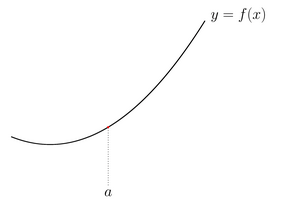
まず仮に上の図のy=f(x)上の点aで接線を引きたいとします。
そこで、接線の傾きを出してみようと思います。
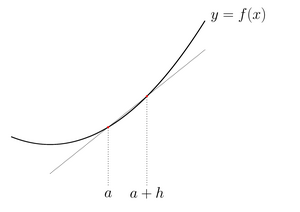
いったん上の図のように点aと点a+hの2点間の傾きを調べてみます。
そうすれば、yの増加量はf(a+h)-f(a)、xの増加量は(a+h)-a=hであるとわかるので、

まず仮に上の図のy=f(x)上の点aで接線を引きたいとします。
そこで、接線の傾きを出してみようと思います。

いったん上の図のように点aと点a+hの2点間の傾きを調べてみます。
そうすれば、yの増加量はf(a+h)-f(a)、xの増加量は(a+h)-a=hであるとわかるので、
が傾きだとわかります。
これはx=aからa+hまでの平均変化率ともいいます。
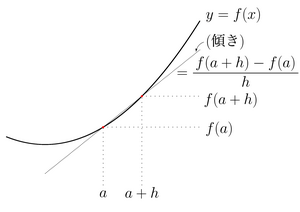
そして、点a+hを上の図でどんどん点aに近づけていくと、a+h≒aとなり、h≒0となれば、この線は接線に近づくはずです。
そうしてでたx=aでの傾きはf'(a)または(f(a))'で表されます。
つまり、接線の傾きは
これはx=aからa+hまでの平均変化率ともいいます。

そして、点a+hを上の図でどんどん点aに近づけていくと、a+h≒aとなり、h≒0となれば、この線は接線に近づくはずです。
そうしてでたx=aでの傾きはf'(a)または(f(a))'で表されます。
つまり、接線の傾きは
の中のhを0に近づけた値です。これをx=aでの微分係数といいます。
しかし、
しかし、
※aは定数
という風に表してしまうと、0で割り算をすることになり、定義不可能になったり、
f(a+0)をf(a)として計算してしまうことも起きてしまいます。
それを防ぐために、「hをめちゃくちゃ(極限まで)0に近づけていった時の、計算の値の変化(ある値への収束)の仕方を見る」という意味で
という風に表してしまうと、0で割り算をすることになり、定義不可能になったり、
f(a+0)をf(a)として計算してしまうことも起きてしまいます。
それを防ぐために、「hをめちゃくちゃ(極限まで)0に近づけていった時の、計算の値の変化(ある値への収束)の仕方を見る」という意味で
を使って
と表します。
具体例としてy=x2でのx=3での微分を行います。

上の図で、点(3,9)と点(3+h,(3+h)2)の平均変化率は
具体例としてy=x2でのx=3での微分を行います。

上の図で、点(3,9)と点(3+h,(3+h)2)の平均変化率は
となるが、hを極限まで0近づけると
となり、x=3での微分係数は3であるとわかりました。
また、今回は3という具体例で計算しましたが、
変数xを使って接線の傾きの関数を求めたい場合はaにxを代入します。
また、今回は3という具体例で計算しましたが、
変数xを使って接線の傾きの関数を求めたい場合はaにxを代入します。
ちなみにこれは導関数といいます。
また、f(x)をk回微分したものは
k個
また、f(x)をk回微分したものは
k個
や、
と表されます。
例えば
例えば
とし、これの導関数を求めると
となることがわかります。
さらに、導関数を求めることは微分といいます。
接線の傾きがわかれば、その時点でどのくらいグラフの増減に勢いがあるのかを調べることができるのでグラフの形を知る上で非常に重要です.
つまり微分をすることで多くの関数のグラフを書くことが出来ます。
さらに、導関数を求めることは微分といいます。
接線の傾きがわかれば、その時点でどのくらいグラフの増減に勢いがあるのかを調べることができるのでグラフの形を知る上で非常に重要です.
つまり微分をすることで多くの関数のグラフを書くことが出来ます。
対数
累乗の逆
23=8は、当然のことですよね。
では、「8は2を何回掛けたものか」を表す数式はどのようなものでしょう。
それこそ、
では、「8は2を何回掛けたものか」を表す数式はどのようなものでしょう。
それこそ、
なのです。
また、8は2を3回かけたものですので
また、8は2を3回かけたものですので
になります。
ほかにも、16は2を4回かけた数であり、先ほどのようにあらわすと、
ほかにも、16は2を4回かけた数であり、先ほどのようにあらわすと、
となります。
そしてある数bに対して
そしてある数bに対して
を計算することを、「bの対数をとる。」また、この時aを対数の底といいます。
ちなみに
ちなみに
は
と表すこともあります。
そしてある数aのln aを求めることを、「自然対数をとる。」といいます。
lnの読み方は「ロン」です。
そしてある数aのln aを求めることを、「自然対数をとる。」といいます。
lnの読み方は「ロン」です。
logの性質
ここで、logに関する面白い性質を紹介します。
まず、
まず、
と定義します。
この時b=acを
この時b=acを
に代入すると、指数法則より
になります。
をこれに代入すると、
となります。つまり
は指数がおりてきて
となります。
超微分編
微分-指数関数編
今回は(ax)'を計算します。
まず、微分の公式に当てはめて
まず、微分の公式に当てはめて
ここで
とします。
つまり
つまり
です。
この時
この時
ですので
です。
よって
よって
となり、これを式変形すると、
そして自然対数をとると、(のちの都合で対数ではなく自然対数とします。)
また、対数の性質
より
という風に、hもtで表せるようになりました。
よって
よって
になります。分母分子にln aをかけると
です。
ここで、eが出てきます。
eの定義を思い出すと
ここで、eが出てきます。
eの定義を思い出すと
ですが、
ですので、
とも書けます。
両辺の自然対数をとると、
両辺の自然対数をとると、
ここで再度
を使うと
となり、結論として
が得られます。
そうすると、
そうすると、
となりますが、
であるため、
になります。
つまり、
つまり、
です。
微分-三角関数
三角関数の極限
x>0かつx[rad]の時下の三角形の体積の関係は
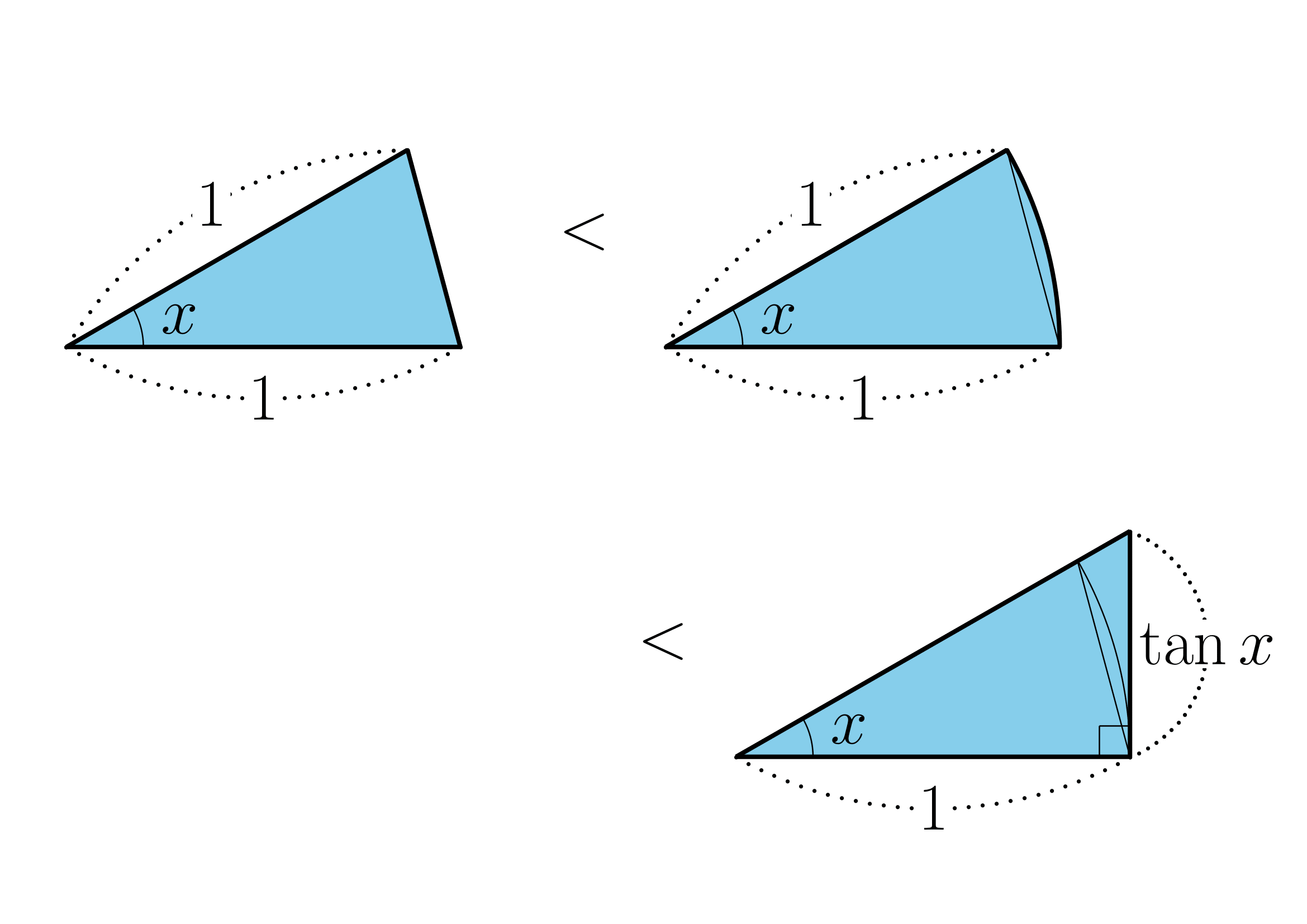
こうなります。
この時それぞれの体積は

こうなります。
この時それぞれの体積は
ですが、
よりsinxで割ると
また、
の時逆数の大小は
のように入れ替わるため
の逆数は
のようになります。
この時

からcos0=1であり、
この時

からcos0=1であり、
ですから、
において
とすると、
imageプラグインエラー : 画像URLまたは画像ファイル名を指定してください。
(http://latex.codecogs.com/png.latex?\lim_{h\to+0}cosh\to1<\frac{sinh}{h}<1
となり
となり
になります。
※h→+0とは、hを正の方向から0に近づけるということを意味します。(h=1,0.1,0.01,0.0001,0.000001・・・のように)
※逆にh→-0とはhを負の方向から0に近づけることを意味します。(h=-1,-0.1,-0.01,-0.001,-0.0001・・・のように)
※h→0はhを正と負どちらの方向からでも近づけてけいさんすることをいみします。(h→±0と書いてもよい)
次に
※h→+0とは、hを正の方向から0に近づけるということを意味します。(h=1,0.1,0.01,0.0001,0.000001・・・のように)
※逆にh→-0とはhを負の方向から0に近づけることを意味します。(h=-1,-0.1,-0.01,-0.001,-0.0001・・・のように)
※h→0はhを正と負どちらの方向からでも近づけてけいさんすることをいみします。(h→±0と書いてもよい)
次に
を計算します。t=-sとすると、
より、
よって同様に
となります。
以上から
以上から
になります。
sinの微分
(sinx)'を計算していきます。
微分の公式から
微分の公式から
より
ここで
より、
なので
さらに
より
また、

より、

より、
であるため
よって
また、
cosの微分
次に(cos)'を計算する。
微分の公式から
微分の公式から
ここで
より、
そして
より
さらに
より
よって
最終奥義【極・微分 】
f(x)=g(x)+i(x)
f(x)=g(x)+i(x)の時のf'(x)を計算する
このように、関数を微分するときは、複数に分解してそれぞれを微分したものを足してもよい。
f(x)=a・g(x)
f(x)=a・g(x)として微分する
つまり、
(xn)'
(xn)'を微分する。
ここで
より
hは0になるので
つまり
さらにnxn-1を微分すると、
より
同様に
つまり
マクローリン展開
マクローリン展開
という風に無限に微分ができる関数があるとします。
この時、当然ですが、f(0)=a1です。
また、
この時、当然ですが、f(0)=a1です。
また、
より
ともかけます。
さらに
さらに
であることから
であり、
同様に
であるため、f(x)は
という風に書けます。
ただしf(x)は無限に微分可能
eの展開
f(x)=exとすると、(ex)'=exより
なので
また、x=1を代入すると
というように、eは、階上の逆数の総和だったことがわかります。
sinの展開
(sinx)'=cosx
(cosx)'=-sinx
(-sinx)'=-cosx
(-cosx)'=sinx
より、sinは無限に微分できることがわかります。
よって
(cosx)'=-sinx
(-sinx)'=-cosx
(-cosx)'=sinx
より、sinは無限に微分できることがわかります。
よって
となります。
この時sinxをn回微分したとき、(sinx,cosx,-sinx,-cosx)のどれかになることがわかります。
表にすると
この時sinxをn回微分したとき、(sinx,cosx,-sinx,-cosx)のどれかになることがわかります。
表にすると
| n | 回 | 微 | 分 | |
| sinx | 0 | 4 | 8 | … |
| cosx | 1 | 5 | 9 | … |
| -sinx | 2 | 6 | 10 | … |
| -cosx | 3 | 7 | 11 | … |
しかし、sin0=-sin0=0となるため、cosxと-cosxについてみます。
| n | 回 | 微 | 分 | |
| cosx | 1 | 5 | 9 | … |
| -cosx | 3 | 7 | 11 | … |
さらにcos0=1,-cos0=-1ですので、
| 自然数k | 0 | 1 | 2 | 3 | 4 | 5 | … | k |
| n回微分 | 1 | 3 | 5 | 7 | 9 | 11 | … | 2k+1 |
| f(k)(0)計算結果 | +1 | -1 | +1 | -1 | +1 | -1 | … | (-1)k |
つまり、
になります。
cosの展開
(cosx)'=-sinx
(-sinx)'=-cosx
(-cosx)'=sinx
(sinx)'=cosx
よりcosxもsinx同様に無限に微分可能であることがわかります。
表にすると
(-sinx)'=-cosx
(-cosx)'=sinx
(sinx)'=cosx
よりcosxもsinx同様に無限に微分可能であることがわかります。
表にすると
| n | 回 | 微 | 分 | |
| cosx | 0 | 4 | 8 | … |
| -sinx | 1 | 5 | 9 | … |
| -cosx | 2 | 6 | 10 | … |
| sinx | 3 | 7 | 11 | … |
しかし、sinxの時同様sin0=-sin0=0となるため、cosxと-cosxについてみます。
| n | 回 | 微 | 分 | |
| cosx | 0 | 4 | 8 | … |
| -cosx | 2 | 6 | 10 | … |
さらにcos0=1,-cos0=-1ですので、
| 自然数k | 0 | 1 | 2 | 3 | 4 | 5 | … | k |
| n回微分 | 2 | 4 | 6 | 8 | 10 | 12 | … | 2k |
| f(k)(0)計算結果 | +1 | -1 | +1 | -1 | +1 | -1 | … | (-1)k |
つまり、
です。
オイラーの等式
ここで重要な3つのパーツがそろいました。
です。
これらは似ていますが、どうも組み合わせれそうないです。
そこで、レオンハルト・オイラーという数学者はある数に注目しました。
それこそ、
これらは似ていますが、どうも組み合わせれそうないです。
そこで、レオンハルト・オイラーという数学者はある数に注目しました。
それこそ、
なのです。
i1=i
i2=-1
i3=-i
i4=1
となりますが、これを
i1=i
i2=-1
i3=-i
i4=1
となりますが、これを
に組み込むんです。
そうすると
そうすると
ここでsinとcosの展開を思い出しましょう。
でしたね。
もうお気づきかもしれませんが、そうなんです。
さっきの式にこれらがぴったりとはまるんです。
つまり、
もうお気づきかもしれませんが、そうなんです。
さっきの式にこれらがぴったりとはまるんです。
つまり、
になるんです!!
そしてそして、x=π[rad]を代入すると、
そしてそして、x=π[rad]を代入すると、
という有名なあの式が出てくるんです。
引用元
- おいしい数学
添付ファイル
- aa.png
- additiontheorem1.png
- additiontheorem2.png
- introduction_of_differential1.png
- introduction_of_differential2.png
- introduction_of_differential3.png
- introduction_of_differential4.png
- limit_sine_over_x.png
- permutation.png
- radian1.png
- radian2.png
- radian3.png
- radian4.png
- reduction-formula-1.png
- reduction-formula-2.png
- reduction-formula-4.png
- sigmaformula.png
- trigonometric-function-01.png
- trigonometric-function-02.png
- trigonometric-function-03.png
- グラフ1.png
- グラフ2.png
- グラフ3.png
