絶対値を含む方程式・不等式(1次式) - 数学 @ ウィキ

方程式の解き方

まず、絶対値を含む方程式を考えます。

このとき、絶対値の定義より、

となります。
ここでは「プラスマイナス」、つまり

の2つの解を持つことを表しています。

なお、もし なら、絶対値が負の数になることはないので解は存在しません。

不等式の解き方

次に、不等式を考えます。
（b ≥ 0 の場合）
絶対値の定義より、

という範囲で解を表すことができます。

この場合も同様に、

となります。

（b ≥ 0 の場合）
絶対値は「大きさ」を表すので、

となります。つまり解は2つの区間に分かれます。

この場合も同様に、

です。

練習問題

以下の方程式，不等式を解け．
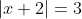
(1)

...

(2)

...

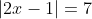
(3)

...

(4)

...

(5)

...

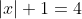
(6)

...

(7)

...