命題の逆・裏・対偶 - 数学 @ ウィキ

ある命題「」に関して

• 「」を逆
• 「」を裏
• 「」を対偶

といいます。
図に表すと

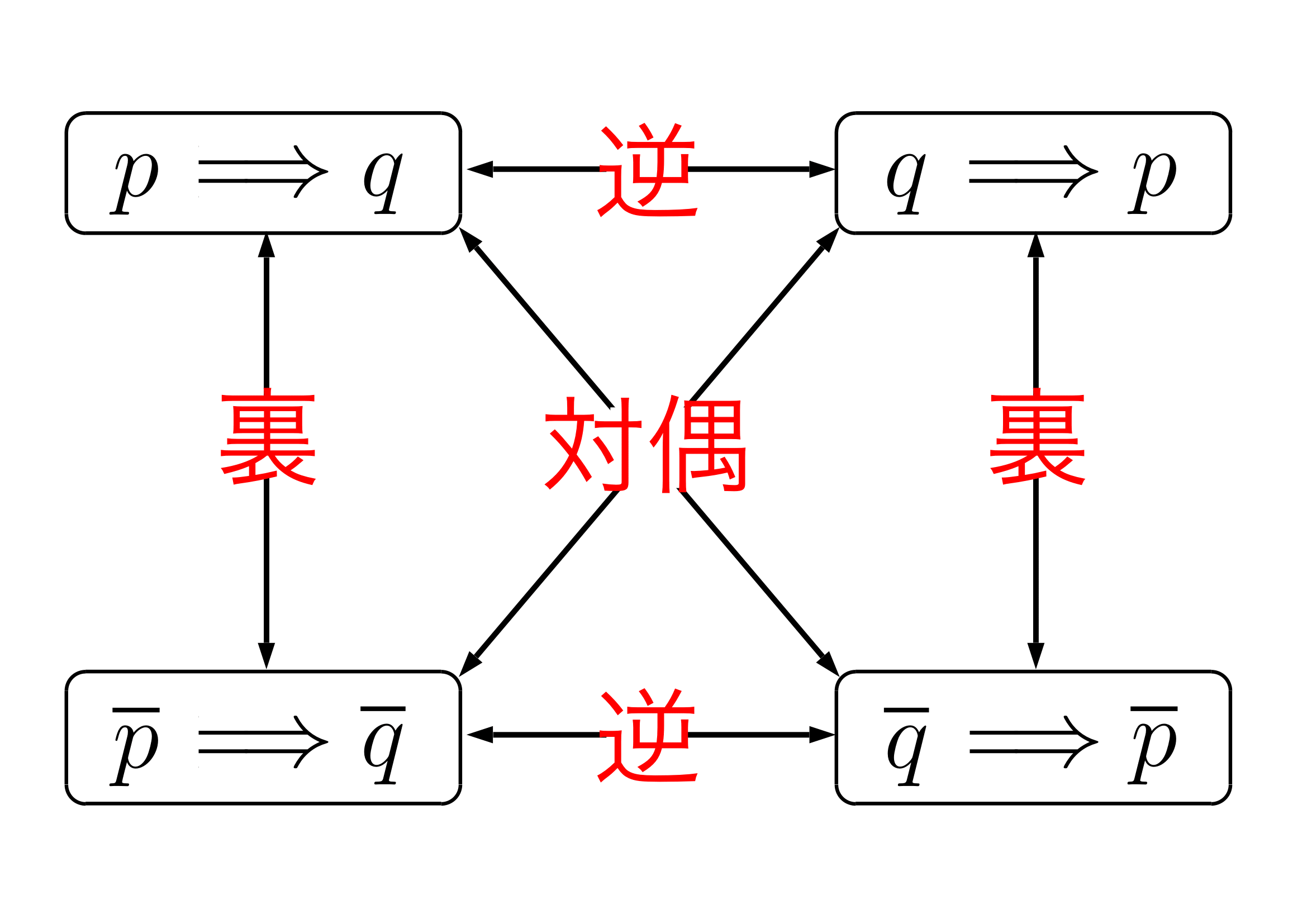
このような関係になります。
この時
命題「」が真ならば

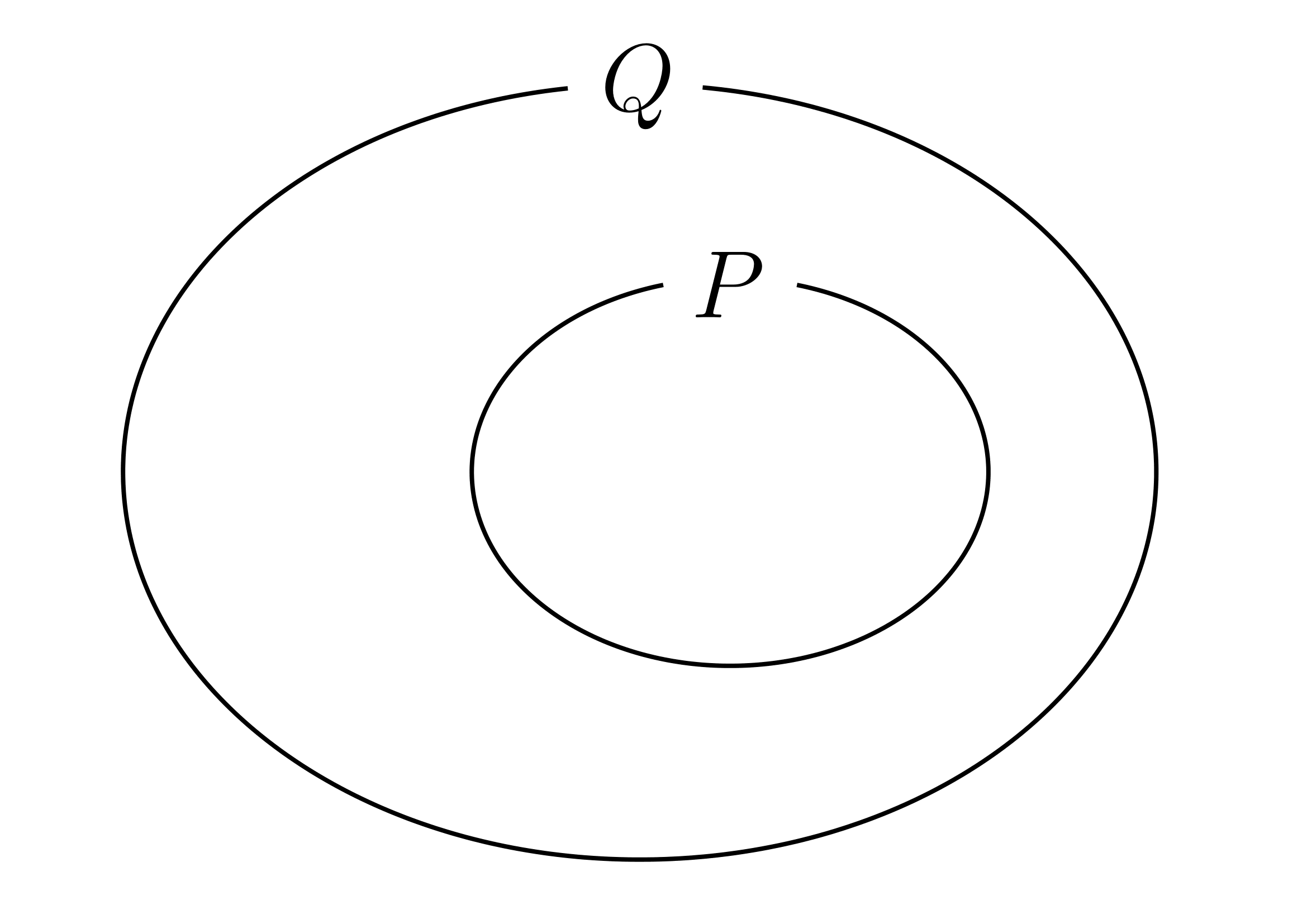
上のようなベン図になり
になります。
これはが成り立つことと同値なので、命題「」は真になります。

元の命題と対偶の真偽は一致する。

これを利用して、元の命題が示しにくいときに対偶を示せば元の命題が証明できることになります。
これを対偶証明法、対偶論法などといいます。

• 元の命題が示しにくいときは対偶を示す。

問題

(1)「x²−x−2<0ならば0<x<1」の逆、裏、対偶を述べ、その真偽を答えよ。

...

逆：「0<x<1ならばx²-x−2<0」

• 真

※P={x|0<x<1}，Q={x|x²−x−2<0}
とすると、
P⊂Qになります。
裏：「x²-x−2≧0ならばx≦0，1≦x」

• 真

※ 逆が真なので、逆にとっての対偶である裏も真です。
対偶：「x≦0，1≦xならばx²−x−2≧0」

• 偽

(反例：x=−12)

(2)n²が偶数ならばnは偶数であることを示せ。

...

対偶：「nが奇数ならばn²が奇数」を示す。
nが奇数ならば、n=2k+1(kは整数)とおける。
n²=4k²+4k+1=2(2k²+2k)+1
よりn²も奇数。
対偶が真なので、元の命題も真。

x，yを実数、a，bを整数とする。以下をこたえよ

(1)「x+y≦3ならば、[x≦1またはy≦2] 」の逆、裏、対偶を述べ、その真偽を答えよ。

...

逆：「[x≦1またはy≦2]ならば、x+y≦3」

• 偽

(反例：x=−1，y=5)
裏：「x+y>3ならば[x>1かつy>2]」

• 偽

(反例：x=−1，y=5)
※ 逆が偽なので、逆にとっての対偶である裏も偽です。
反例も一致します。
対偶：「[x>1かつy>2]ならばx+y>3」

• 真

(2)abが3の倍数ならばa，bの少なくとも一方は3の倍数であることを示せ。

...

対偶：「a，bがともに3の倍数でないならばabが3の倍数でない」を示す。
k，lを整数とする．
(ⅰ)a=3k+1，b=3l+1のとき
ab=9kl+3k+3l+1=3(3kl+k+l)+1
(ⅱ)a=3k+1，b=3l+2のとき
ab=9kl+6k+3l+2=3(3kl+2k+l)+1
(ⅲ)a=3k+2，b=3l+1のとき
ab=9kl+3k+6l+1=3(3kl+k+2l)+2
(ⅳ)a=3k+2，b=3l+2のとき
ab=9kl+6k+6l+4=3(3kl+2k+2l+1)+1
以上より対偶が真なので、元の命題も真。