集合
数学では、奇数列や素数列などの、「数列」といったものや、「チンパンジー、ゴリラ、オランウータン」などの分類されたある集まりについて扱うことがあります。
例えば、奇数列
例えば、奇数列
- 1,3,5,7,9,・・・
などがありますが、これを数学では
と{}で囲って表します。
また、動物の集合は
また、動物の集合は
- {チンパンジー、ライオン、キリン、ゾウ、ニンゲン、・・・}
と表します。
しかし、世の中には「何もない」も集合としてカウントします。
つまり
しかし、世の中には「何もない」も集合としてカウントします。
つまり
という集合もあるわけです。
これは∅(空集合)といいます。
また、「Aを偶数列とする」と、Aには「2」や「4」が含まれます。
これを数学では
これは∅(空集合)といいます。
また、「Aを偶数列とする」と、Aには「2」や「4」が含まれます。
これを数学では
という風に表します。
また、「2と4は、Aの要素である」とも言います。
また、Aには「1」や「5」は含まれません。
これを先ほどのようにあらわすと
また、「2と4は、Aの要素である」とも言います。
また、Aには「1」や「5」は含まれません。
これを先ほどのようにあらわすと
といった具合に表します。
そして先ほど同様「1と5は、Aの要素でない」といいます。
集合の定義の仕方は「Aを偶数列とする」以外にもあって、
そして先ほど同様「1と5は、Aの要素でない」といいます。
集合の定義の仕方は「Aを偶数列とする」以外にもあって、
という表し方もあります。
また、数学には特定の集合を以下のようにあらわします。
また、数学には特定の集合を以下のようにあらわします。
- 自然数
- 整数
- 有理数
- 実数
- 複素数
| + | 余談 |
これより∅(空集合)は
と表されます。
これを使うと、偶数列Aは
これを使うと、偶数列Aは
というようにあらわせます。
また、B={サルの集合}とすると、「B∉ライオン」というのもわかりますね。
このようにB={サルの集合},C={動物の集合}とすると、サルはすべて動物ですから、図にすると、
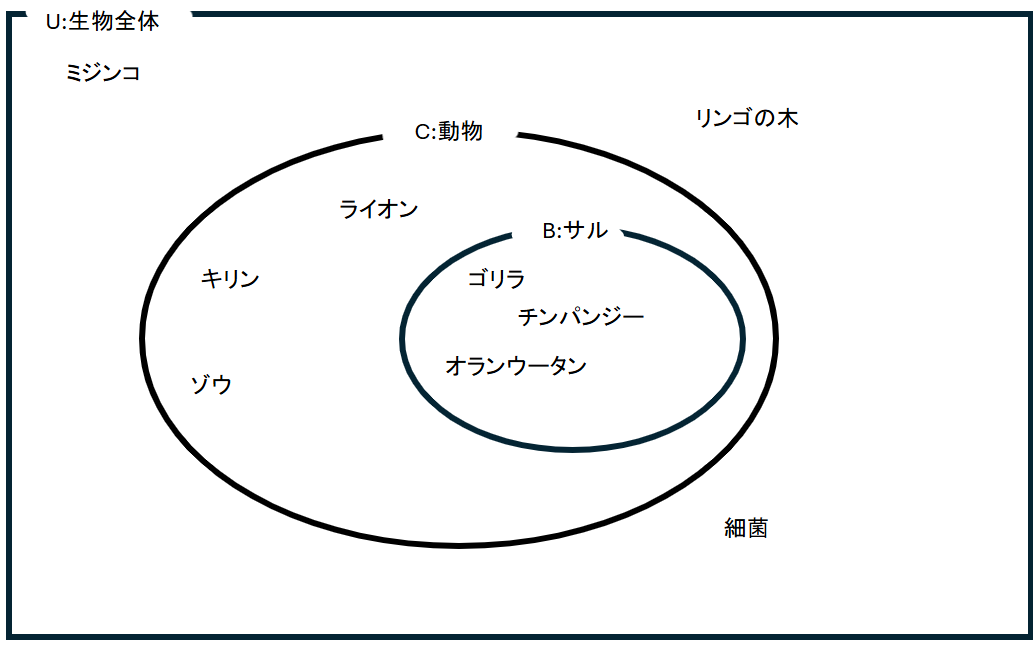
このようになります。
ちなみに上の図はベン図といいます。
そして数学では集合も含めた全体の集合(上のベン図で言うと生物すべての集合)は基本的にUで表され、全体集合といいます。
また、B={サルの集合}とすると、「B∉ライオン」というのもわかりますね。
このようにB={サルの集合},C={動物の集合}とすると、サルはすべて動物ですから、図にすると、

このようになります。
ちなみに上の図はベン図といいます。
そして数学では集合も含めた全体の集合(上のベン図で言うと生物すべての集合)は基本的にUで表され、全体集合といいます。
集合の重なり
では次に、
- U={1~20}
- A={2の倍数}
- B={3の倍数}
とすると、
となりますが、これらの集合は
という要素が重なっています。
この重なっている部分を数学では
この重なっている部分を数学では
と表します。
つまり今回だと
つまり今回だと
です。
このように、AとBの重なったところを「AかつB」といいます。
また、AとBを合体させた集合
このように、AとBの重なったところを「AかつB」といいます。
また、AとBを合体させた集合
を
で表します。
ちなみにこれは「AまたはB」です。
そして先ほど同様
ちなみにこれは「AまたはB」です。
そして先ほど同様
です。
しかしここで、
しかしここで、
- C={7の倍数}とすると、
ですが、この時のBかつCは
であるため、
つまり空集合になります。
部分集合

この図で、Bのすべての要素をCは含みます。(サルは動物であるため。)
なので、あいまいで不適切な表現ですが、「集合Bは集合Cの要素である」という風に解釈できます。
しかし、数学ではこれを「集合Bは集合Cの部分要素」と表現します。
つまり、「集合Cの一部分が集まった集合」みたいな意味です。
そしてこれは
という風に表します。
ちなみにこの時
ちなみにこの時
(BかつCはB)
(BまたはCはC)
です。
です。
補集合
数学には
- A=偶数の集合
としたとき、
となる集合Bが存在します。
これを
これを
(Aバー)
と表します。
今回の場合
と表します。
今回の場合
- A=奇数の集合
ですね。

で言うと、

で言うと、
はキリンやゾウ、リンゴなどサルでない生物を要素に持ちますね。
また、発展として
また、発展として
はサルでない動物の集合を表しています。
そして、
そして、
や、
という性質があります。
そしてさらに
そしてさらに
です。
ド・モルガンの法則
めんどいので
です。
代わりに証明やりたい人がいたら書いてください。
今僕は「花粉症か風邪」なので、だるいのでもっとだるいことはしたくないからです
代わりに証明やりたい人がいたら書いてください。
今僕は「花粉症か風邪」なので、だるいのでもっとだるいことはしたくないからです
要素の個数
Aの要素の個数がx個あるとき、
という風に表します。
添付ファイル
