2次関数の最大最小(グラフ変動・定義域固定) - 数学 @ ウィキ

2次関数の最大最小

2次関数のグラフが動いて定義域が固定のタイプの最大最小問題です。
本格的に場合分けが必要になるので、最初につまづく人は多いのではないでしょうか。
このページではスライド表示を用いて丁寧に説明します。

問題に触れ、学ぶ

まずは何を言っても複雑だろうと思ったので、例題を解いて、何をする問題か一緒に学びましょう。

例題☆-1

関数ただしの最小値mを求めよ。

まずはとりあえず脳死で平方完成をしてみましょう。
平方完成をすると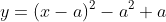になり軸はx=aです。
軸にaという文字が入っているので、aの値に応じてグラフを横に変動させます。
すると以下のようになります。

...

画像が止まった場合閉じてもう一度開いたら動きます。

※(実際には上下にも動きますが，最大最小に影響ないので無視します)
グラフが下に凸のときの最小値(上に凸のときは最大値)は、軸が定義域の左か、定義域内か、定義域の右かで場合分けをします。
※定義域とはのような、xの取れる範囲を意味します。
では上の図を場合分けして解いていきます。
(i)a<−2の時

...

a<-2の時グラフは

でありx=-2でyの最小値

(ii)の時

...

...

画像が止まった場合閉じてもう一度開いたら動きます。
)の時グラフは

でありでの最小値

(iii)4<aの時

...

4<aの時グラフは

でありx=4でyの最小値

(i),(ii),(iii)より

例題☆-2

関数ただしの最大値Mを求めよ。

例題1と同じように左右に変動させて考えます。

...

画像が止まった場合閉じてもう一度開いたら動きます。

最大値はx=−2またはx=4のときになりそうですがどこが境目でしょうか。
グラフが下に凸のときの最大値(上に凸の場合いの最小値)は、軸が定義域の中心(今回はx=1)の右か左かで場合分けをします。
(ⅰ)a<1の時

...

a<1の時グラフは

...

画像が止まった場合閉じてもう一度開いたら動きます。

で最大値Mはx=4の時のyになり

(ii)a=1の時

...

a=1の時グラフは

で最大値Mはx=-2,4の時のyになり

(iii)a>1の時

...

a>1の時グラフは

...

画像が止まった場合閉じてもう一度開いたら動きます。

で最大値Mはx=-2の時のyになり

(i),(ii),(iii)より

問題

関数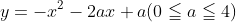に関して以下の問いに答えよ

(1)最大値Mを求めよ
(2)最小値mを求めよ

...

とする。
平方完成をすると
^2+a^2+a)で、軸はx=-a
(1)
(i)-a<0の時、a>0でy=f(x)のグラフは以下のようになる。

この時

(ii)の時、となりこの時f(x)のグラフは以下のようになる。

この時

(iii)-a>4の時、a<-4でy=f(x)のグラフは以下のようになる。

この時

(i),(ii),(iii)より