線形軸と対数軸

　ヒトの可聴域は、周波数20Hz-20000Hz（20kHz）と広範囲であり、対数軸を用いることで広大なダイナミックレンジを表現できる。
（線形軸では、低周波数に合わせるとスケールが広大で高周波数がオーバーし、、高周波数に合わせると低周波数のスケールが潰れてしまう）
　ヒトは、周波数が2倍となることで音の高さが2倍になって聞こえるため、等比数列的な関係性がある。
（周波数が2倍になると、音の高さは1オクターブ上がる）
　1オクターブの間は12音階に分かれており、隣接する音階は2^(1/12)倍になっている。

---

• 線形軸：差が等間隔の目盛りになっている軸

例）
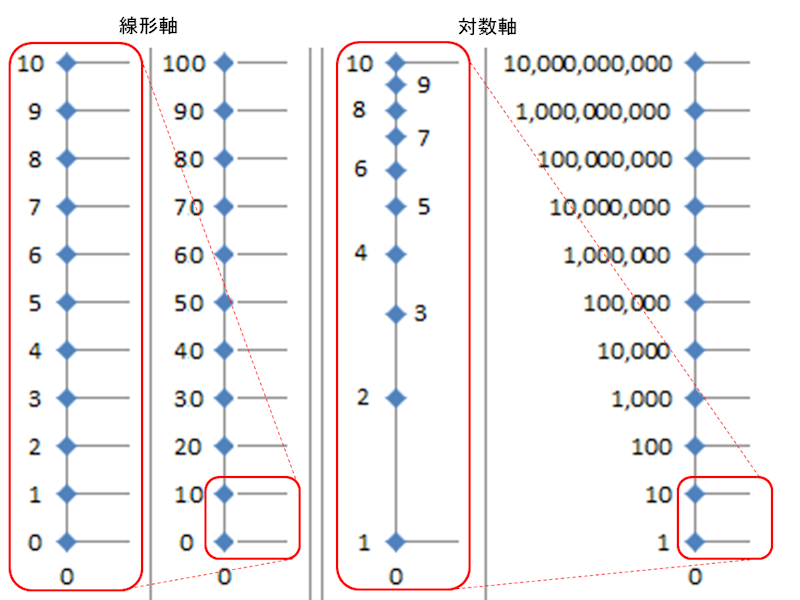
　0 - 10 - 20 - 30 -
　差が10で等間隔

• 対数軸：比が等間隔の目盛りになっている軸

例）
　1 - 10 - 100 - 1000 -
（10^0 - 10^1 - 10^2 - 10^3 -）
　比が10で等間隔

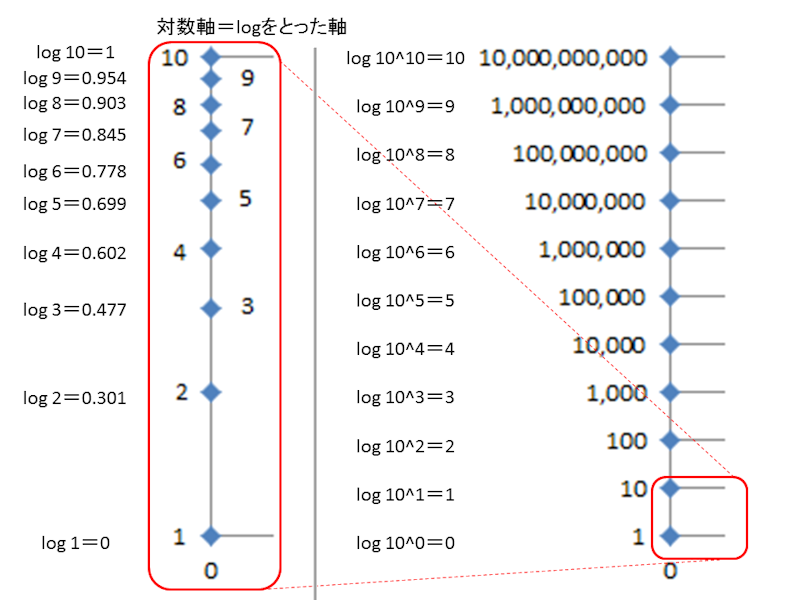
• 対数軸＝線形軸の常用対数（底が10の対数）をとったもの

例）
　log 10^0 - log 10^1 - log 10^2 - log 10^3 -
（0 - 1 - 2 - 3 -）
　比の対数の差が1で等間隔

　対数軸では、1 - 2 - 3 -の間隔は、等間隔でない
　log 1 - log 2 - log 3 -
　（log 2－log 1）≠（log 3－log 2）

　対数軸では、1 - 2 - 3 -の間隔と、10 - 20 - 30 -の間隔が等しい
　log 10 - log 20 - log 30 -
（log 1×10 - log 2×10 - log 3×10 -）
（log 1＋log 10 - log 2＋log 10 - log 3＋log 10 -）

→10 - 20 - 30 -の目盛り間の差は、log 1 - log 2 - log 3 -の目盛り間の差と等しい
　（log 2＋log 10）－（log 1＋log 10）＝log 2－log 1
　（log 3＋log 10）－（log 2＋log 10）＝log 3－log 2

---

---