<波形解析の方法>
①まず、音楽ファイルを用意します。
③用意した音楽ファイルを、WAVファイルへ変換します。
⑤変換したWAVファイルを、さらにテキストデータのCSVへ変換します。
WAVファイルは短時間に膨大なデータが密に詰め込まれているので、切り出す区間を決めて短時間の波形を切り抜きます。
「開始時刻」と「終了時刻」を設定して、「変換実行」します。
これで、エクセルで利用することができるデータとなりました。
⑥エクセルで開くと、1列目に時間、2列目にLch、3列目にR chの順で並んでいます。
短時間のファイルでも、膨大な行のデータになっています。
データを選択して、「折れ線グラフ」を描画します。
図1)
グラフの各系列(波形)は、上から順に、
系列1(灰色):生データを正規化(最大値で割って、0-1の範囲に変換)
系列3(水色):系列1のデータを2乗
系列4(赤色):系列1のデータを3乗
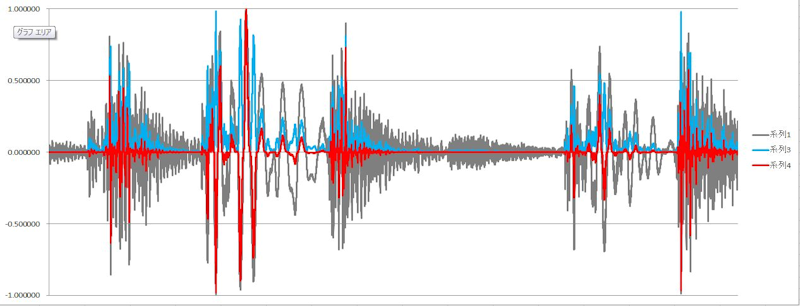
2乗、3乗となるにつれて、波形が先鋭化するのが分かります。
べき乗では、絶対値が小さい値はより小さくなり、絶対値が大きな値はより大きくなるためです。
ここで、あらかじめ1以下に正規化してあるために、最大値1を超えることはありません。
つまり、小さな基線
ノイズを0に近似して、ピーク値を誇張する作用があります。
2乗の場合は、必ず正になってしまうため、絶対値のグラフと比較した方が良いかもしれません。
図2)
グラフの各系列(波形)は、上から順に、
系列1(紫色):生データを正規化(最大値で割って、0-1の範囲に変換)して絶対値化
系列2(緑色):生データを正規化(最大値で割って、0-1の範囲に変換)して絶対値化したものを負数化
系列3(水色):生データを正規化(最大値で割って、0-1の範囲に変換)したものを2乗
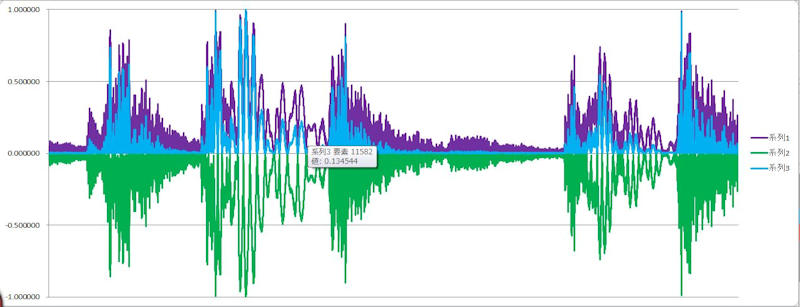
絶対値化の波形では、負数の生データがX軸を対象に正方向に折り返されています。
2乗の波形は、絶対値の波形と全体像がそれほど変わりませんが、変化がより誇張された形になってします。
なお、2乗の波形も絶対値化と同様、負数が存在しません。
図3)
①系列1-4
グラフの各系列(波形)は、上から順に、
系列1(灰色):生データを正規化(最大値で割って、0-1の範囲に変換)
系列2(橙色):系列1において、前値からの差分(現在値から前値を減算)
系列3(水色):系列2を正規化(最大値で割って、0-1の範囲に変換)したものを3乗
系列4(赤色):系列1を3乗
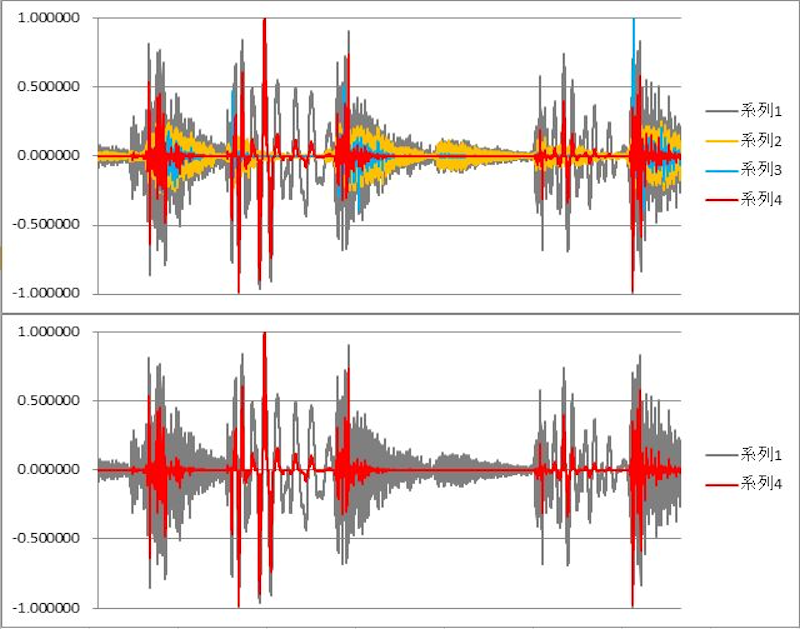
②系列1と系列4:元の波形と3乗の波形
3乗を行うことで、正負の符号を保存したままで、グラフの尖度を上げることができます。
③系列1と系列2:元の波形と微分(差分法)の波形
差分は、一定の短時間における変化量のため、一定間隔で現在値から前値を差し引いた差分は、離散的な微分グラフとなります。
(連続的な微分グラフは、無限小の短時間における変化量を表します)
差分は常に絶対値の減少方向へ向かうため、+1→+1で差分0,+1→0で差分1,+1→-1で差分2と、差分は0-2の範囲に収まります。
(ほとんどの場合、ごく短時間における差分は1/2振幅以下で推移するようですので、振幅2倍表示した方が見やすいかもしれません。
④系列2と系列3:微分(差分法)の波形と微分(差分法)の3乗の波形
3乗を行うことで、正負の符号を保存したままで、グラフの尖度を上げることができます。
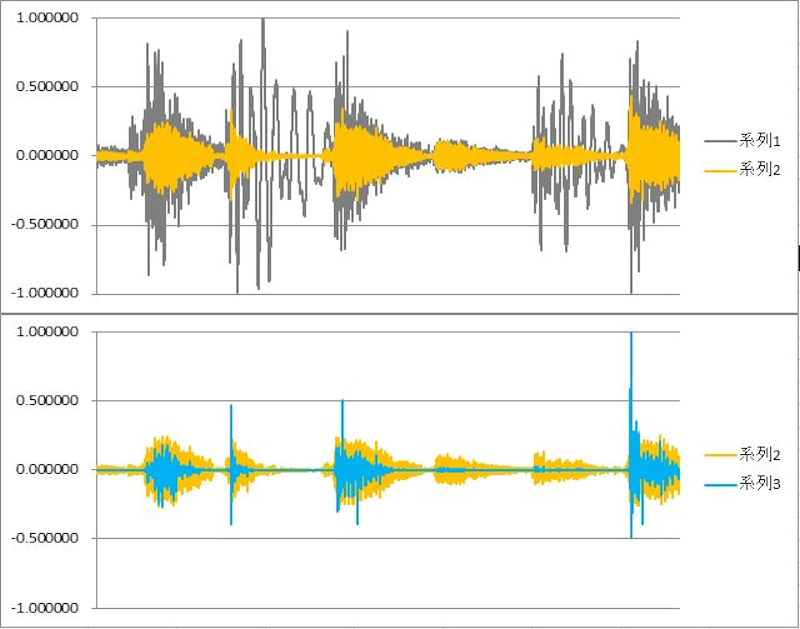
図4)
グラフの各系列(波形)は、上から順に、
系列1(青色):生データを正規化(最大値で割って、0-1の範囲に変換)
系列2(赤色):系列1において、開始時からの累積値(現在値に前値を加算)
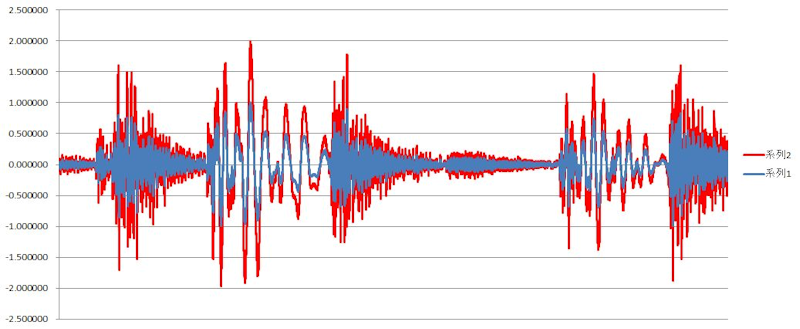
現在値に一定の短時間における増分を加算していくと、累積値(グラフ下面積)となり、離散的に積分グラフになります。
(連続的な積分グラフは、無限小の短時間における変化量を表します)
正負はそのままで加算するため、負値の累積的な加算は、X軸より下のグラフ下面積を減算することになります。
(グラフ下面積は、X軸とグラフに挟まれる領域の面積のため、X軸より下のグラフでは、正確にはグラフ上面積です)
正負に平等に振れる振動では、X軸より上のグラフ下面積と、X軸より下のグラフ下面積はほぼ相殺され、2倍振幅をほとんどオーバーしません。
図5)
グラフの各系列(波形)は、上から順に、
系列1(灰色):生データを正規化(最大値で割って、0-1の範囲に変換)
系列2(水色):系列1の2乗(平方)
系列3(紫色):系列1の絶対値を1/2乗(平方根)
系列4(緑色):系列1を絶対値化
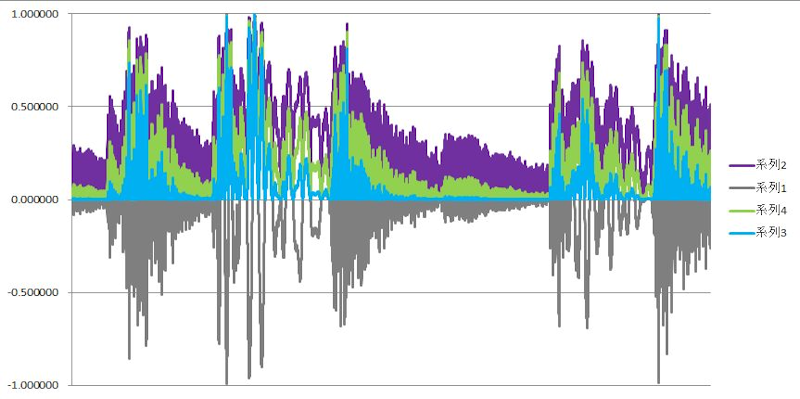
平方(2乗)では、グラフはピークが尖鋭化して、裾は基線に近付きます。
グラフはピークを保ったまま、基線の方向に圧縮され、差が拡大されます。
平方根(1/2乗)では、グラフのピークが鈍化して、裾はピークに近付きます。
グラフはピークを保ったまま、最大振幅の方向に拡張され、差が縮小され、全体的に均一化されます。
<べき乗値について>
X^n(Xのn乗)において、n=0ではX=1となり、n<0では(1/X)^(ABS(n))=(Xの逆数 ^ nの絶対値)になります。
n>1では、0<X<1においてX^n<Xとなり、X>1においてX<X^nとなります。
0<n<1では、0<X<1においてX<X^nとなり、X>1においてX^n<Xとなります。
n>1では、nが偶数の場合は、X^n≧0となります。
0<n<1では、1/n(nの逆数)が偶数の場合は、X≧0である必要があります。
最終更新:2013年09月16日 02:18





