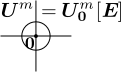コメント
- トップページ/フォームから
こんにちは。 -- (132人目の素数さん) 2008-06-26 20:30:00- レステスト - 2008-06-26 20:34:52
- トップページ/携帯用から こんばんわ。 - 2008-06-26 20:30:00
- atwikiイイ(・∀・)! -- (132人目の素数さん) 2008-07-01 09:29:43
-
-- (名無しさん) 2009-01-25 02:41:32
- こんにちは。
ちょっと疑問に思ったのですが、m次元ユークリッド空間のn次元単体は、m×n行列でなく、m×(n+1)行列とすべきではないのでしょうか?。
m×n行列とするのは、平行移動させたものは同じと考えるということになると思います。
それなら、回転させたもの、つまり、m次の正規直交行列を掛けたものも同じと考えるべきでは?。
というようなことを思ったのですが、いかがでしょうか?。 -- (hiraishi) 2009-05-15 19:29:54 - hiraishiさんありがとうございます!
今ここでは、n次元単体を作る(n+1)個の頂点をi点(i=0…n)と呼び、このi点からn次元単体の五心などを求める表記の方法として、
m次元ユークリッド空間の原点から各i点へのm次元位置ベクトルを列挙したm×(n+1)の位置行列
を用いる位置表記、もしくは、
n次元単体の0点から各i点(i=1…n)へのm次元方向ベクトルを列挙したm×nの方向行列
を用いる方向表記、の約2通りを使っております。
ご指摘のとおり、m×n行列とする方向表記の場合は、平行移動を無視し、さもn次元単体の0点がm次元ユークリッド空間の原点と言わんばかりの解法になります。
一年前は、この計算が比較的楽な方向表記でしか定式化できていなかったため、トップページなどでもm×n行列と断言してしまってますが、m×(n+1)行列を用いる表記も言うべきでした。
メールした広義垂心の導出もm×(n+1)行列を用いた位置表記だと綺麗な式にならなそうだったので、3×3行列の方向表記を用いて逆にわかりずらく楽をしていました。
普通、多変量解析などの問題で「m個の値を持つバラバラな(n+1)点の全てに等距離な点(n次元単体の外心)を求めよ」とかありそうで、
平行移動だけならn点から1点の座標引いて後に足して戻す感じで公式化できますが、回転や鏡映しても同じn次元単体だからといって、
わかりやすい性質の正単体や直交単体となって解けるわけではないので、私的には方向表記か位置表記の公式とするしか思い浮かびませんでした。
まとめると、n次元単体の五心の公式などで定式化するのに、位置表記もしくは平行移動だけ無視した方向表記が適していると考えており、
n次元単体としての形が変わらない回転や鏡映など変換するとき、公式から五心などが求まっていれば一緒に変換して導出できるというような感じです。
質問にうまく答えれなかった気もしますので、またご質問して下さると嬉しいし、またメールします! -- (neetubot) 2009-05-21 03:10:49 - ゴメンナサイ…見づらい…
m×(n+1)行列を用いる位置表記は、
(n+1)本の位置ベクトルのうち1本分が
一次従属になるときもあるから難しいけど、
最近けっこう計算できるようになってきました。
m次の正規直交行列をとすれば、
n次元単体の方向行列と同じ形のn次元単体は、
m×(n+1)行列で位置表記でき、
このときn次元単体の重心の方向表記をとすれば、
で位置表記されるn次元単体の重心は
と書けるみたいな
ことが言いたかった。… -- (neetubot) 2009-05-21 03:31:10 - m次の正規直交行列を掛けたものも同じn次元単体になりますが、
n次元単体の五心などを導出するのにm×n行列を用いると比較的簡単で、
これからはちゃんとしたm×(n+1)行列を用いた解法の方もがんばりたい。
平行移動しても同じではなく、厳密に位置が指定されたn次元単体から、
平行移動して0点を原点とみなして五心などを計算してから、
もとの0点の位置まで逆の平行移動で五心などを含めて戻せば、
その厳密に位置が指定されたn次元単体の五心などを求めるのと同じ、みたいな -- (neetubot) 2009-05-21 03:53:09 - 今日は、Inkscapeとpstoeditというフリーソフトを使って図を描いてみました。
昔はUnixでtgif使ってましたが、Windowsでちゃんとできる環境が整いました。
その内消すかもですが、少し下に載せておきます。
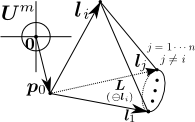
左から、原点を通りm次単位行列を基底とするm次元ユークリッド空間
、
内で原点から
の点を始点とするn次元基底
(n次元単体の方向表記)、
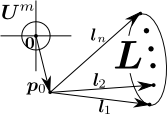
内で(n+1)個の点
(i=0…n)がn次元単体を作るときのm×(n+1)位置行列
、
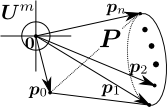
方向行列位置行列
のn次元単体が存在するn次元部分空間(線型部分空間ではない?)
、
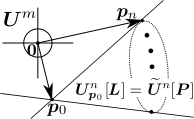
一番右は、n次元単体の方向表記で1本のベクトルとそれ以外のi対面
を分けた図です。
自分の中では、わかりやすい呼び方と記法と図を編み出したなどと思ってますが、いや、なんでもないです… -- (neetubot) 2009-05-22 07:34:40 - 「n次元単体の幾何」の位置行列の成分が添え字1から始まってますが、添え字0からの間違いではないでしょうか? -- (konishi) 2010-09-21 21:53:32
- konishiさん大変ありがとうございます!
直しました!私は今は和算に目覚めて、
【和算もオッサンも】▲初等幾何スレッド2●【代数で解析】
などやったりしておりました。
http://kamome.2ch.net/test/read.cgi/math/1284618538/l50 -- (neetubot) 2010-10-01 22:57:48 - 私,小西さんに興味が有り,
neetubot(at)gmail.comまで
ご連絡頂けるとありがたいです. -- (neetubot) 2010-10-12 08:43:52