アットウィキロゴ
NEETUBOTの完全座標幾何学
アットウィキロゴ
NEETUBOTの完全座標幾何学
ページ一覧

このページは、 平石司さん「高次元単体の諸心」 のオイラー線以降に則して、ベクトル解法などします。



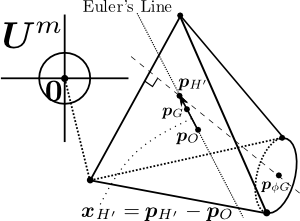
n次元単体におけるオイラー線上の点


m次元ユークリッド空間内で位置行列\mathbf{P}=[\mathbf{p}_0,\cdots,\mathbf{p}_n]で表されるn次元単体\tilde{A}^n[\mathbf{P}]のオイラー線上の点は、外心\mathbf{p}_O=\mathbf{p}_y+\mathbf{P}^\ddagger \tilde{\mathbf{b}}_O（ただし、\tilde{\mathbf{b}}_O = \begin{pmatrix} \mathbf{p}_0^T \mathbf{p}_{0} \\ \vdots \\ \mathbf{p}_n^T \mathbf{p}_{n} \end{pmatrix} \frac{1}{2}）と重心\mathbf{p}_G=\frac{\mathbf{P} \tilde{\mathbb{1}}}{n+1} = \mathbf{p}_y+\mathbf{P}^\ddagger \tilde{\mathbf{b}}_G（ただし、\tilde{\mathbf{b}}_G = \frac{\mathbf{P}^T \mathbf{P}\tilde{\mathbb{1}}}{n+1}）を結ぶ直線上の点であり、任意の実数αを用いて次式の位置ベクトルで表される。 

\mathbf{p}_O + \alpha (\mathbf{p}_G - \mathbf{p}_O) = \mathbf{p}_y+\mathbf{P}^\ddagger (\alpha \tilde{\mathbf{b}}_G + (1-\alpha) \tilde{\mathbf{b}}_O)

等内積単体における垂心・重心・外心の位置


n次元単体が、垂心\mathbf{p}_Hの存在する等内積単体（直辺単体・垂心単体）\mathbf{P}^T \mathbf{P} = \tilde{\mathbf{N}}となるとき、外心は\mathbf{p}_O = \frac{\mathbf{P} \tilde{\mathbb{1}}}{2} - \left(\frac{n-1}{2}\right) \frac{\mathbf{P} {\small \begin{pmatrix} \frac{1}{\nu_0} \\ \vdots \\ \frac{1}{\nu_n} \end{pmatrix}}}{\tilde{\mathbb{1}}^T {\small \begin{pmatrix} \frac{1}{\nu_0} \\ \vdots \\ \frac{1}{\nu_n} \end{pmatrix}}} = \frac{n+1}{2} \mathbf{p}_G - \frac{n-1}{2} \mathbf{p}_Hとなるので、次式のように垂心は外心と重心を(n+1)：2に外分するオイラー線上の点であると言える。 

\mathbf{p}_H = \mathbf{p}_O + \frac{n+1}{n-1} (\mathbf{p}_G - \mathbf{p}_O)（ただし、\mathbf{P}^T \mathbf{P} = \tilde{\mathbf{N}}のときに限る。）

n次元単体における広義垂心


任意のn次元単体においても、外心と重心を(n+1)：2に外分するオイラー線上の点は常に存在し、これを広義垂心（モンジュ点）\mathbf{p}_{H'}と呼び次式で表す。ここで、n次元単体のi頂点以外の(n-1)次元部分単体（i対面）の重心を\mathbf{p}_{iG} = \frac{\mathbf{P} (\tilde{\mathbb{1}} - \tilde{\mathbf{e}}_i)}{n}として、\tilde{\mathbf{b}}_{H'} = \begin{pmatrix} \mathbf{p}_0^T \mathbf{p}_{0G} \\ \vdots \\ \mathbf{p}_n^T \mathbf{p}_{nG} \end{pmatrix} \left(\frac{n}{n-1}\right)とする。 

\mathbf{p}_{H'} = \mathbf{p}_O + \frac{n+1}{n-1} (\mathbf{p}_G - \mathbf{p}_O) = \mathbf{p}_y+\mathbf{P}^\ddagger \tilde{\mathbf{b}}_{H'}

n次元単体の(n-2)次元部分単体φの重心\mathbf{p}_{\phi G}=\frac{\mathbf{P} (\tilde{\mathbf{1}}-\tilde{\mathbf{e}}_i-\tilde{\mathbf{e}}_j)}{n-1}から広義垂心への直線と、φの部分対面（対辺）は垂直(\mathbf{p}_{H'}-\mathbf{p}_{\phi G})^T (\mathbf{p}_i-\mathbf{p}_j) = 0となる性質が、任意のφで成り立つ。

n次元単体における広義垂心向外線ベクトル


n次元単体の外心から広義垂心へのベクトルを広義垂心向外線\mathbf{x}_{H'}=\mathbf{p}_{H'} - \mathbf{p}_Oと呼び、次式で表す。 

\mathbf{x}_{H'} = \frac{n+1}{n-1} (\mathbf{p}_G - \mathbf{p}_O) = \mathbf{P}^\ddagger (\tilde{\mathbf{b}}_{H'}-\tilde{\mathbf{b}}_O)

n次元単体におけるk次面重心球面の存在条件


n次元単体のk次元部分単体φの重心\mathbf{p}_{\phi G}=\frac{\mathbf{P} \tilde{\mathbf{\delta}}_\phi}{\tilde{\mathbb{1}}^T \tilde{\mathbf{\delta}}_\phi}からの距離r_{Q_k}が全てのφで等しくr_{Q_k}^2=(\mathbf{p}_{Q_k}-\mathbf{p}_{\phi G})^T (\mathbf{p}_{Q_k}-\mathbf{p}_{\phi G})となるとき、\mathbf{p}_{Q_k}=\mathbf{p}_y+\mathbf{P}^\ddagger \tilde{\mathbf{b}}_{Q_k}から半径r_{Q_k}でn次元単体と同じ部分空間に作られる(n-1)次元超球をk次面重心球面と呼ぶ。このとき、
r_{Q_k}^2-\tilde{\mathbf{b}}_{Q_k}^T \mathbf{P}^\dagger \mathbf{P}^\ddagger \tilde{\mathbf{b}}_{Q_k}+\frac{|[\mathbf{P}^T \mathbf{P}]|}{\tilde{\mathbb{1}}^T \mathbf{C}[\mathbf{P}^T \mathbf{P}] \tilde{\mathbb{1}}}=\mathbf{p}_{\phi G}^T \mathbf{p}_{\phi G}-2 \tilde{\mathbf{b}}_{Q_k}^T \frac{\mathbf{P}^\dagger \mathbf{P} \tilde{\mathbf{\delta}}_\phi}{\tilde{\mathbb{1}}^T \tilde{\mathbf{\delta}}_\phi}=c
とすれば、\frac{\tilde{\mathbf{\delta}}_\phi^T \mathbf{P}^T \mathbf{P} \tilde{\mathbf{\delta}}_\phi}{2(k+1)}-\frac{k+1}{2}c=\tilde{\mathbf{\delta}}_\phi^T \mathbf{P}^T \mathbf{P}^\ddagger \tilde{\mathbf{b}}_{Q_k}=\tilde{\mathbf{\delta}}_\phi^T \tilde{\mathbf{b}}'_{Q_k}と書けて、
\tilde{b}'_{j Q_k}=\frac{\left(\sum_{i\in\phi(\not\ni j)} \tilde{\mathbf{\delta}}_{j(\phi\ominus i)}^T \tilde{\mathbf{b}}'_{Q_k}\right)-k \tilde{\mathbf{\delta}}_\phi^T \tilde{\mathbf{b}}'_{Q_k}}{k+1}となるため、
\tilde{b}'_{j Q_k}=\frac{\left(\sum_{i\in\phi(\not\ni j)} \tilde{\mathbf{\delta}}_{j(\phi\ominus i)}^T \mathbf{P}^T \mathbf{P} \tilde{\mathbf{\delta}}_{j(\phi\ominus i)}\right)-k\tilde{\mathbf{\delta}}_\phi^T \mathbf{P}^T \mathbf{P} \tilde{\mathbf{\delta}}_\phi}{2(k+1)^2}-\frac{c}{2}である。

\tilde{b}'_{j Q_k}=\frac{\mathbf{p}_j^T \mathbf{p}_j}{2(k+1)} +\frac{({}_{(n-1)} C_k) \left( 2(k+1)n \mathbf{p}_j^T \mathbf{p}_{jG} - (\mathbf{P}^T \mathbf{P} - \mathbf{\Sigma}[\mathbf{P}^T \mathbf{P}]) \right)}{2 (k+1)^2 ({}_n C_{(k+1)})} -\frac{c}{2} 

\mathbf{p}_{Q_k}=\mathbf{p}_O+\frac{k}{k+1} \mathbf{x}_{H'}, r_{Q_k}=\frac{r_O}{k+1}

n次元単体におけるk次究点（平石さんのメールより）



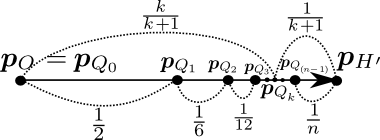
n次元単体においてk次面重心球面の中心に相当する、k次究点\mathbf{p}_{Q_k}を次式で表す。 

\mathbf{p}_{Q_k}=\mathbf{p}_O+\frac{k}{k+1} \mathbf{x}_{H'}=\mathbf{p}_y+\mathbf{P}^\ddagger \left(\frac{k\tilde{\mathbf{b}}_{H'}+\tilde{\mathbf{b}}_O}{k+1}\right)

k=\frac{n-1}{2}のとき、\mathbf{p}_{Q_k}=\mathbf{p}_O+\frac{n-1}{n+1}\mathbf{x}_{H'}=\mathbf{p}_Gとなる。また、\lim_{k\to\infty} \mathbf{p}_{Q_k}=\mathbf{p}_{H'}とも考えられる。

n次元単体におけるk次究点の性質


タグ：

広義オイラー線 広義垂心 等内積単体
+ タグ編集
  • タグ：
  • 広義オイラー線
  • 広義垂心
  • 等内積単体
タグの更新に失敗しました
エラーが発生しました。ページを更新してください。
ページを更新
「オイラー線」をウィキ内検索
最終更新：2009年07月29日 00:45