判別式 - 数学 @ ウィキ

ページ概要

判別式とその関連問題を扱います

判別式

2次方程式の解の公式

において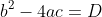とすると、

となる

• の時

xの値は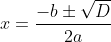の2つある。
つまりの実数解が2つある。

• の時

xの値はの一つのみである。
つまりの解は一つである。
この解を重解と呼ぶ。

• の時

は実数でないためxの値は存在しない。
つまりの実数解は存在しない。

このようにDという値が2次方程式ではよく重要な値になります。
そして、数学ではのことを判別式といい、よくDを使って表されます。
わざわざ解の公式をすべて適用するまでもなく、判別式だけで実数解の個数を判定できる気軽さに判別式を利用するメリットがあります。

2次方程式の判別式をとする。

の時は2つの異なる実数解を持つ。

の時は重解を持つ。

の時は実数解を持たない。

※実数解・・・実数の解　重解・・・2つの重なった解(つまり実数解は1個)

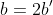2次方程式2次方程式でとした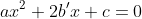の解の公式

のについても判別式と同様のことが言えます。
また、この時の判別式Dを計算するととなり、ちょうどがと一致します。
しかし、実数解の個数はどちらでも調べられます。
このように、少し計算を楽にできるというものも存在します。

問題

(1)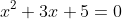の実数解の個数を求めろ。

...

の判別式をDとする。※このDの宣言がないと数Ⅰでははねられます。

よって

は実数解を持たない。

(2)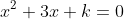の実数解の個数を求めろ。

...

の判別式をDとする。

(i)の時
かつは実数解を2つもつ。
(ii)の時
かつは重解を持つ。
(iii)の時
かつは実数解を持たない。

(i),(ii),(iii)より

は

の時実数解を2つもち、の時重解を持ち、の時実数解を持たない。

(3)2次方程式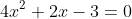の実数解の個数を求めろ

...

の判別式をDとする。

は異なる2つの実数解を持つ。

(4)２次方程式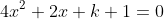の実数解の個数を求めろ

...

の判別式をDとする。

の実数解の個数は
(i)の時、
で２個
(ii)の時、で1個
(ii)の時、で0個

(i),(ii),(iii),より

2次関数は

の時実数解を2個持ち、で重解を持ち、で実数解を持たない。