概要
正弦定理を扱います。
余弦定理と並び三角比分野で重要な定理です。
余弦定理と並び三角比分野で重要な定理です。
正弦定理
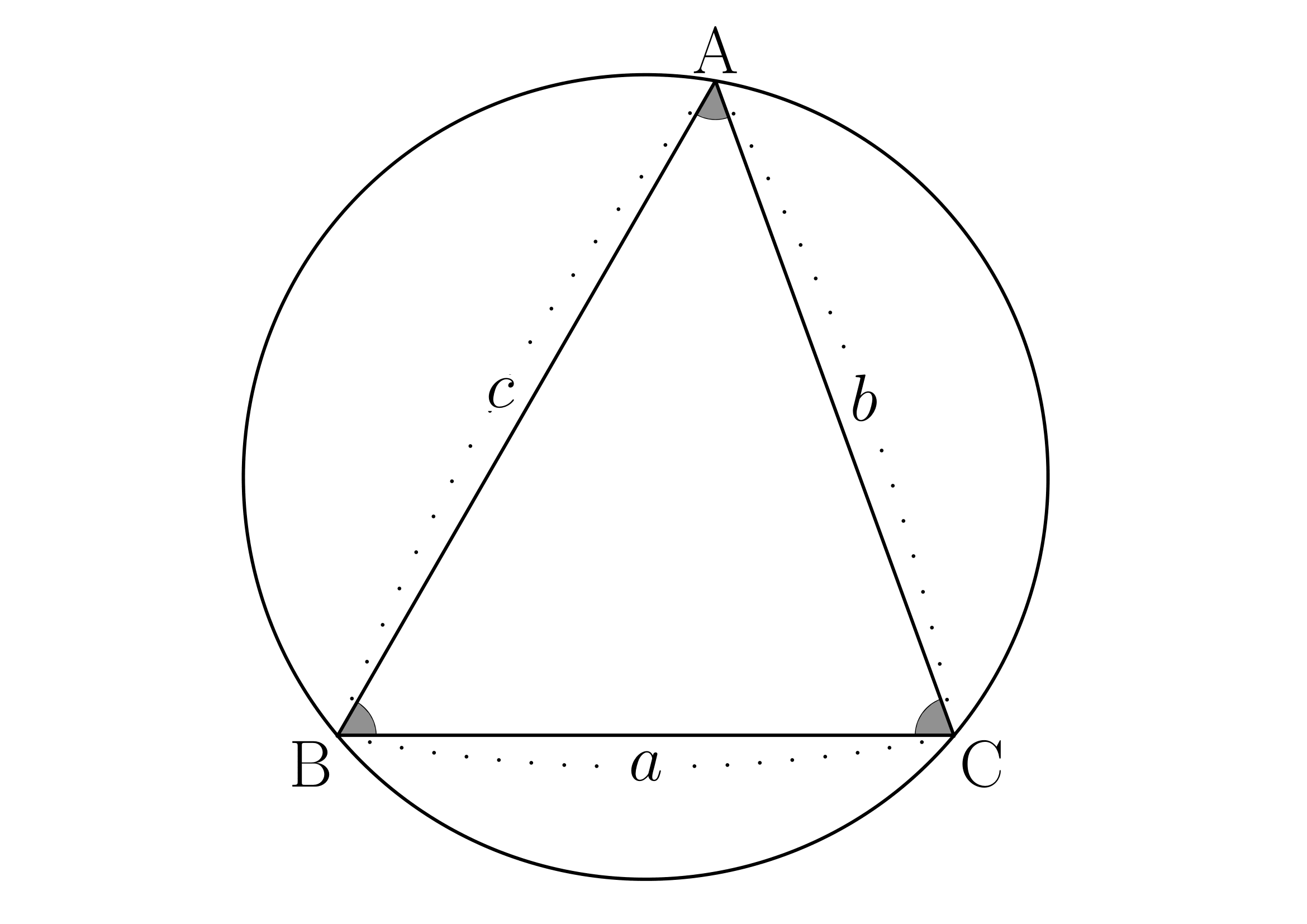
三角形
となる
( i )
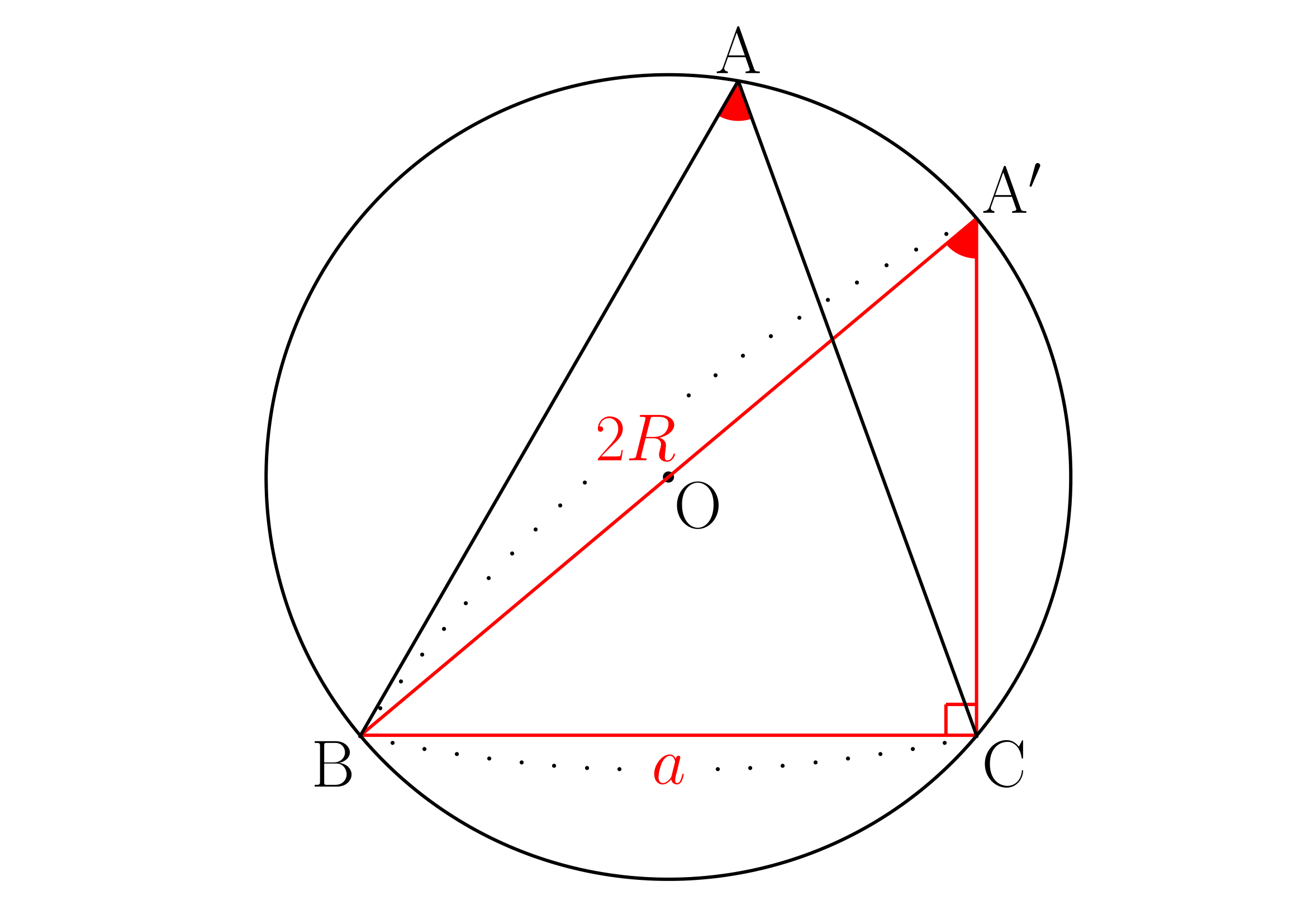
この時
よって
ここから
(i i)
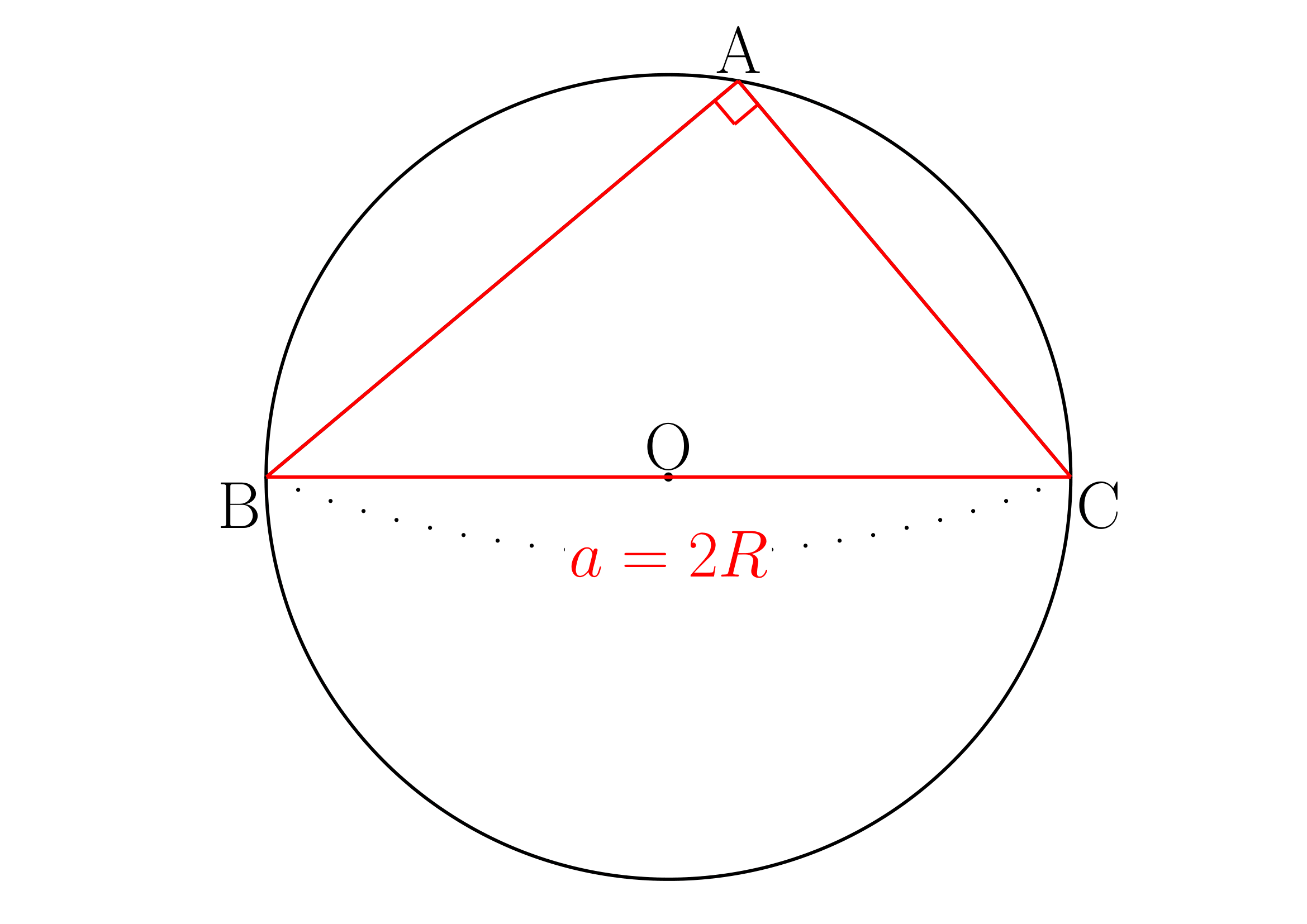
よって
(iii)
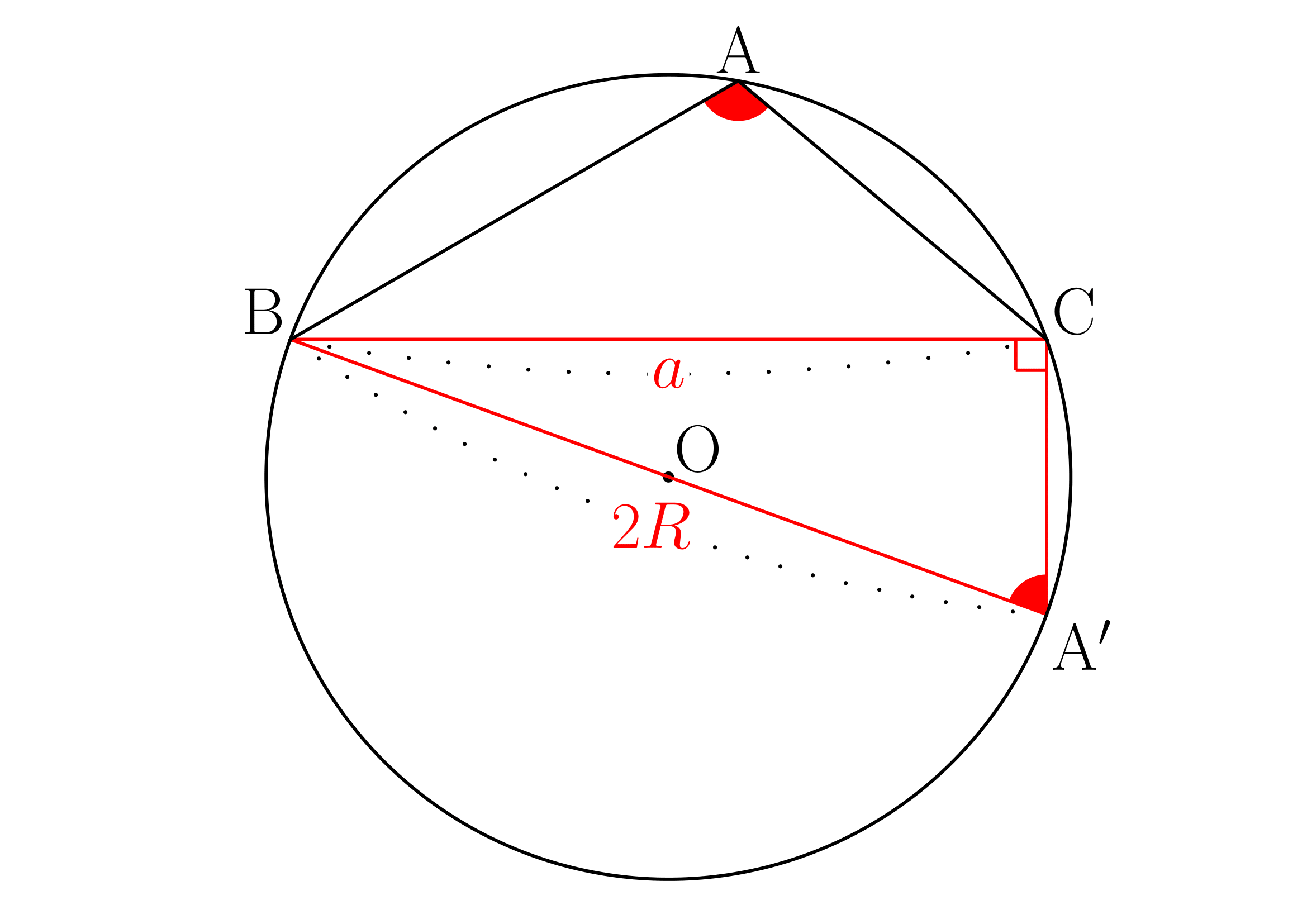
また、還元公式(数Iまたは数II)や円に内接する四角形の対角の和が180°より
よって
これより、
( i )~(iii)より、
同様の証明で
 と
と も示せます。
も示せます。
よって
よって
三角形の外接円の半径を
とすると、以下が成り立つ。

※一般に三角形 で
で






と表します。
と表します。
問題
 において、外接円の半径を
において、外接円の半径を とする。
とする。
(1) の時、
の時、 と
と を求めよ。
を求めよ。
| + | ... |
(2) の時、
の時、 を求めよ。
を求めよ。
| + | ... |
 において、外接円の半径を
において、外接円の半径を とする。
とする。
(1) の時、
の時、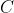 と
と を求めよ。
を求めよ。
| + | ... |
(2) が成り立つとき、
が成り立つとき、 の形をこたえよ。
の形をこたえよ。
