概要
数列
偶数の数列があるとき、その数列の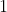 番目を「偶数の数列の
番目を「偶数の数列の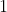 番目」と、無駄に長く書かずに
番目」と、無駄に長く書かずに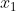 のようにあらわす方法が数学にあります。
のようにあらわす方法が数学にあります。
一般的に 番目の偶数は
番目の偶数は であらわされます。そして、ここで
であらわされます。そして、ここで 番目の偶数を
番目の偶数を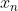 と表すことにすると、
と表すことにすると、 になります。
になります。
つまり、 としたとき偶数列は
としたとき偶数列は
 で表されます。
で表されます。
一般的に
つまり、
数列の和
今まで奇数の1からn番目までの和は、 のように書いていました。しかし、いちいち
のように書いていました。しかし、いちいち と書くのは面倒です。
と書くのは面倒です。
そこで、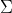 が使われます。
が使われます。
前提として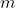 番目の奇数を
番目の奇数を で表すことにします。
で表すことにします。
この時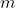 番目の帰数は
番目の帰数は です。
です。
まず、この式は1番目の数からn番目の数まであり、 です。
です。
この時、 に
に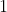 から
から まで代入
まで代入 の
の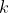 に
に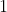 から
から まで代入してすべて足す
まで代入してすべて足す のようにあらわせると便利です。しかし、いちいち「
のようにあらわせると便利です。しかし、いちいち「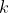 に
に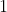 から
から まで代入」と書くのは面倒です。そこで「
まで代入」と書くのは面倒です。そこで「 に
に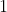 から
から まで代入
まで代入 」の代わりの表し方として「
」の代わりの表し方として「 」とされています。
」とされています。
つまり、奇数列 の
の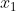 から
から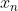 までの足し算は
までの足し算は で表されます。
で表されます。
また、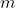 番目の帰数は
番目の帰数は であることから、
であることから、
 で奇数列の
で奇数列の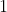 番目から
番目から 番目の数までの和を表します。
番目の数までの和を表します。
そこで、
前提として
この時
まず、この式は1番目の数からn番目の数まであり、
この時、
つまり、奇数列
また、
と
は整数で、
の時

| + | より厳密な定義 |
Σの性質
また、
つまりこれらのことから
| + | より厳密な証明 |
