2次関数の決定 - 数学 @ ウィキ

2次関数を導く

2次関数の決定について扱います。
通る点から逆算をしてどのようなグラフになるかを考えます。
少しバリエーションがありますが一通りの問題を扱います。

2次関数の決定の仕方

与えられた条件を満たす2次関数を求める問題を考えます。
問題によって頂点がわかったり、通る3点がわかったり様々で、条件に応じて以下の中から使う2次関数のタイプを決めると楽に問題が解けます。

• 軸または頂点がわかっているとき

・・・基本形

• 通る点3点がわかっているとき

・・・一般形

• x切片(x軸との交点)がわかっているとき

例題

次の条件を満たす放物線をグラフにもつ2次関数を求めよ。
(1)点(1,-1)を頂点とし、点(3,7)を通る。

...

頂点が(1,-1)より関数は

これが(3,7)を通るので



よって関数は

(2)3点(1,4)(-1,6)(2,6)を通る。

...

3点通るので求める関数をとすると、

• (1,4)を通るので

• (-1,6)を通るので

• (2,6)を通るので

よって

これを解いて
よって求める関数は

(3)３点(1,0)(2,0)(0,2)

...

(-1,0)(2,0)というx切片がわかっているのでとおく。
これが(0,2)を通るので


これより

問題

次の条件を満たす放物線をグラフにもつ2次関数を求めよ。

(1)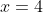を軸とし、点，を通る

...

求めるグラフは軸がx=4より求める関数をとする。
これがとを通るので、


よって

これを解いて
これより求める関数は

(2)3点を通る。

...

求める関数をとすると、これが三点を通るので

これを解いて
よって求める関数は

(3)3点を通る。

...

x切片がより求める関数をとおくと、これがを通るので、

よってこれより求める関数は

(4)x=−1で最大値1をとり、原点を通る。

...

xが実数でyの最大値があるのはグラフが上に凸の場合のみ。
また、その時が最大値。
よって求める関数は
これが原点を通るので
よって
これより求める関数は

(5)放物線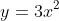を平行移動した曲線で、頂点が
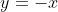上にあり、点を通る。

...

求める関数の頂点のx座標をtとおくと、頂点は上にあるので頂点の座標は。
また、求める関数はを平行移動した図形であるので求める関数をとおく。これがを通るので-t=12-12t+3t^2-t=3t^2-13t+12)


よって求める関数は