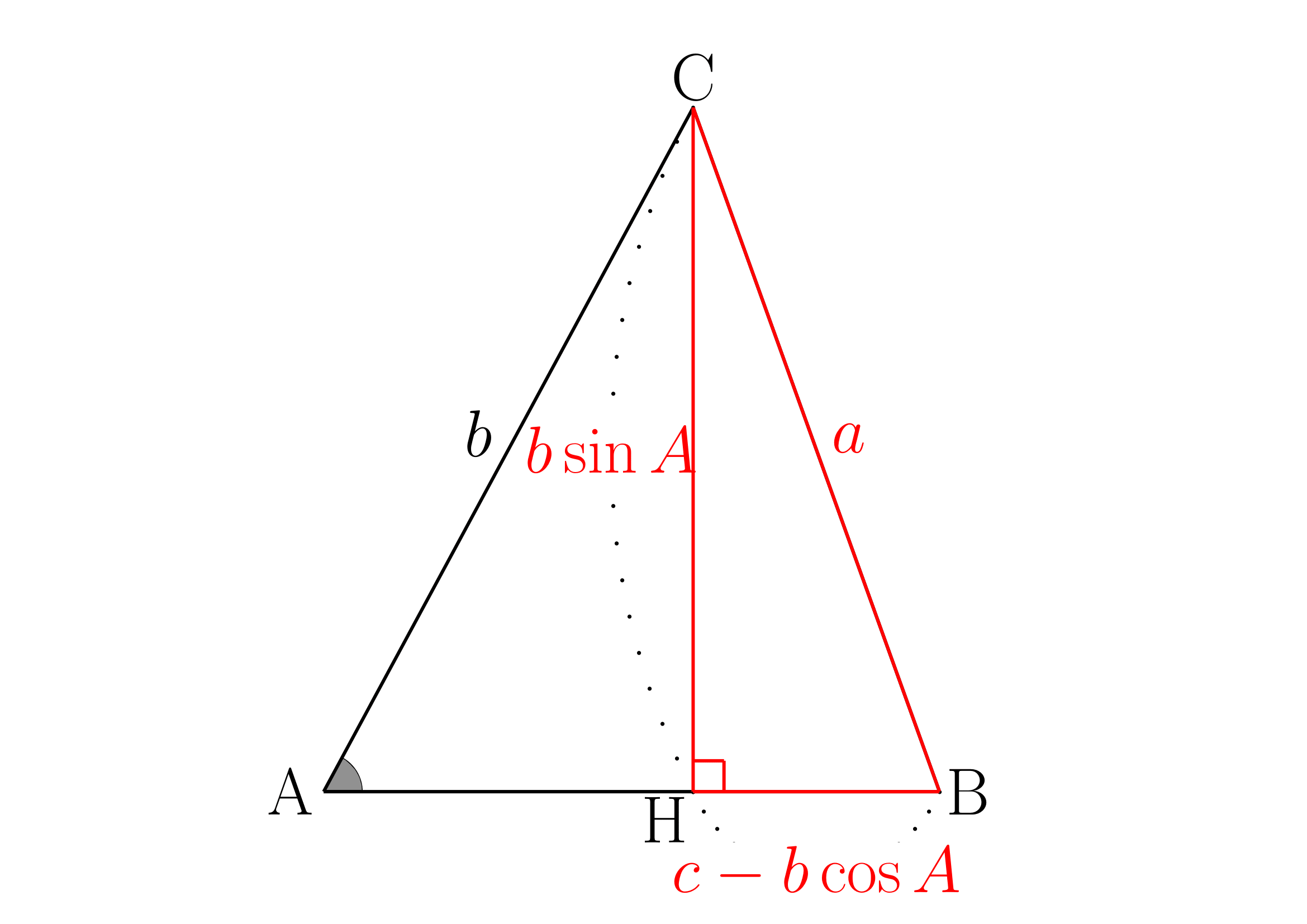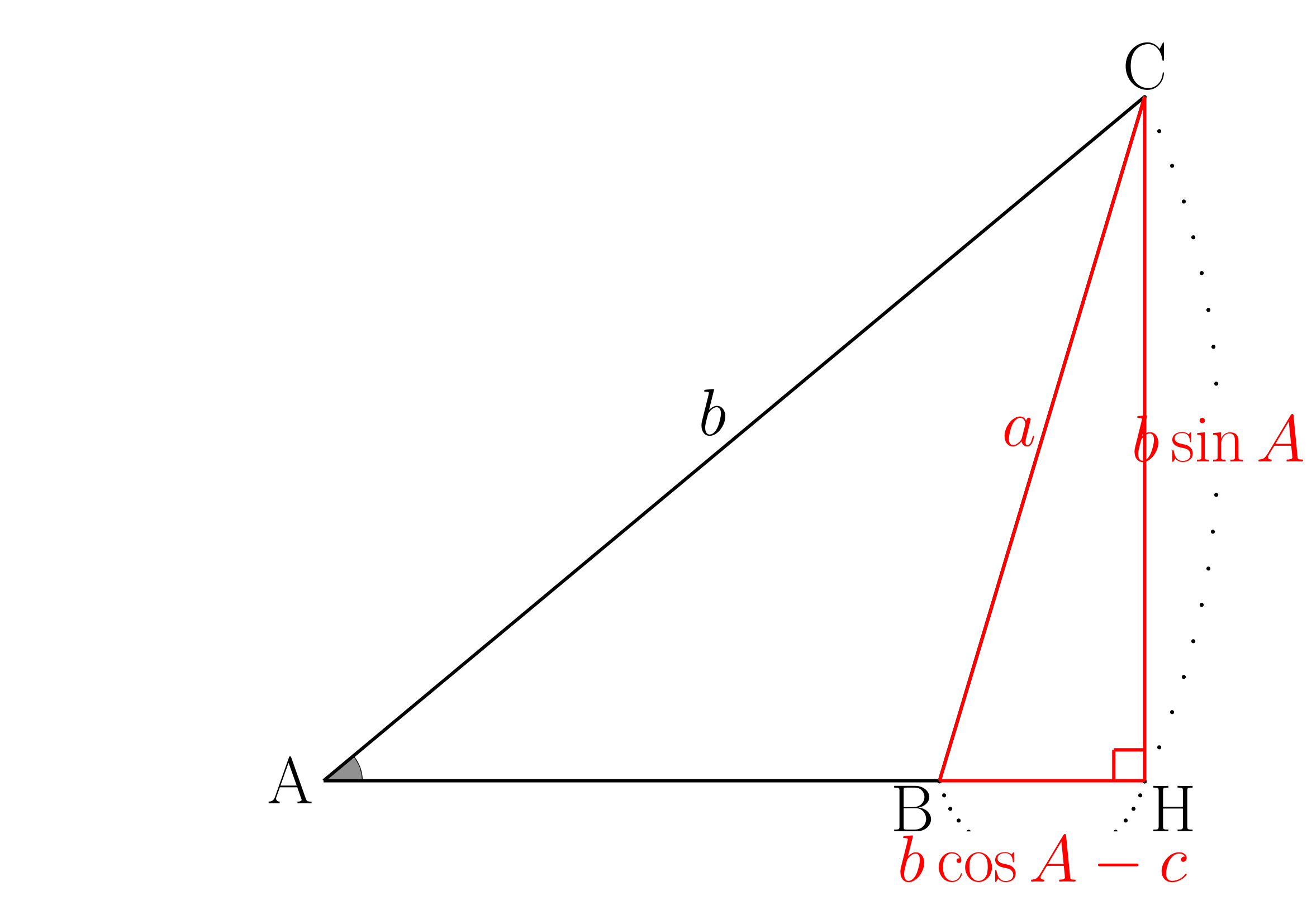概要
余弦定理を扱います。
後半では正弦定理を使った複合的な問題も含めて扱います。
後半では正弦定理を使った複合的な問題も含めて扱います。
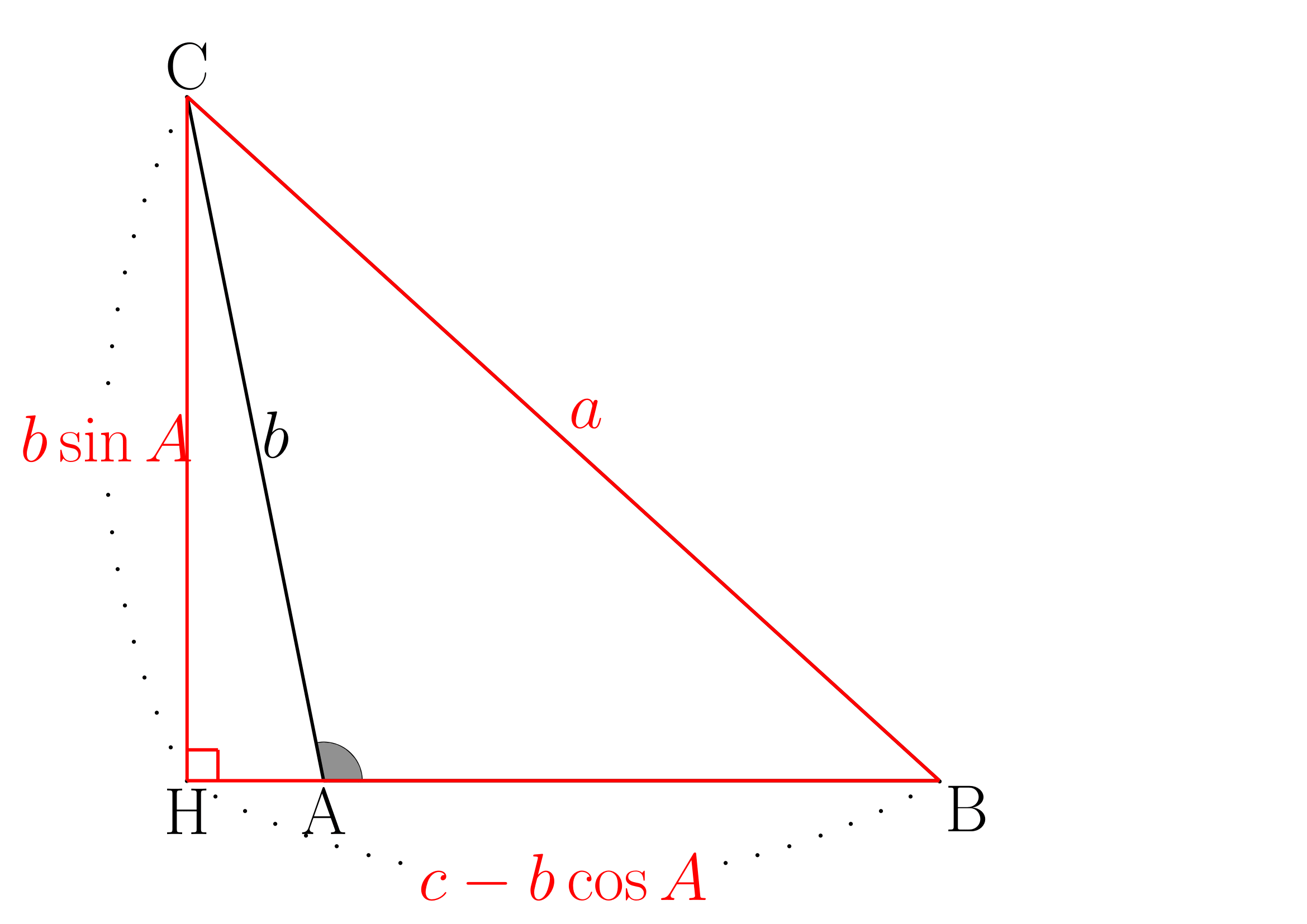
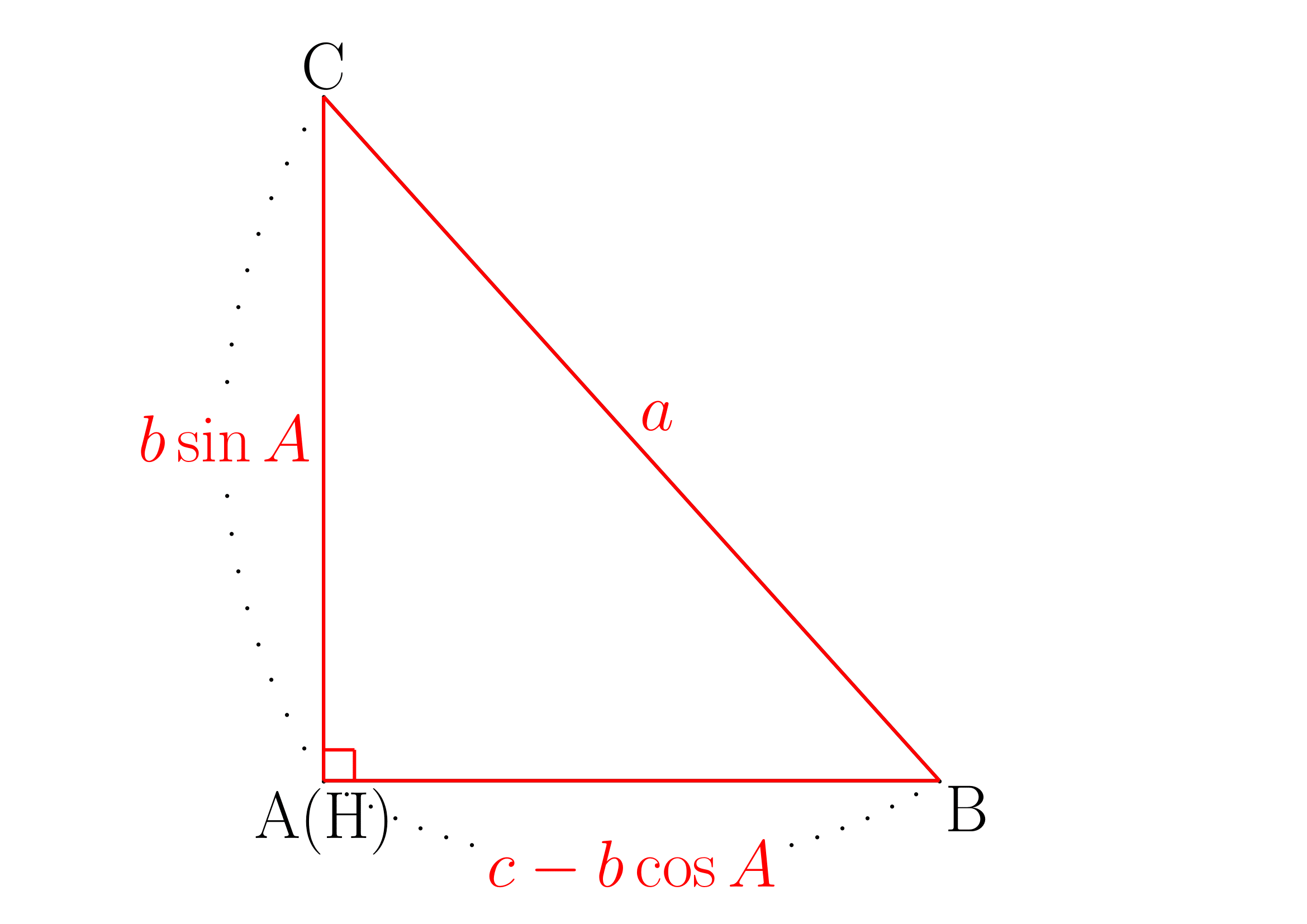
余弦定理
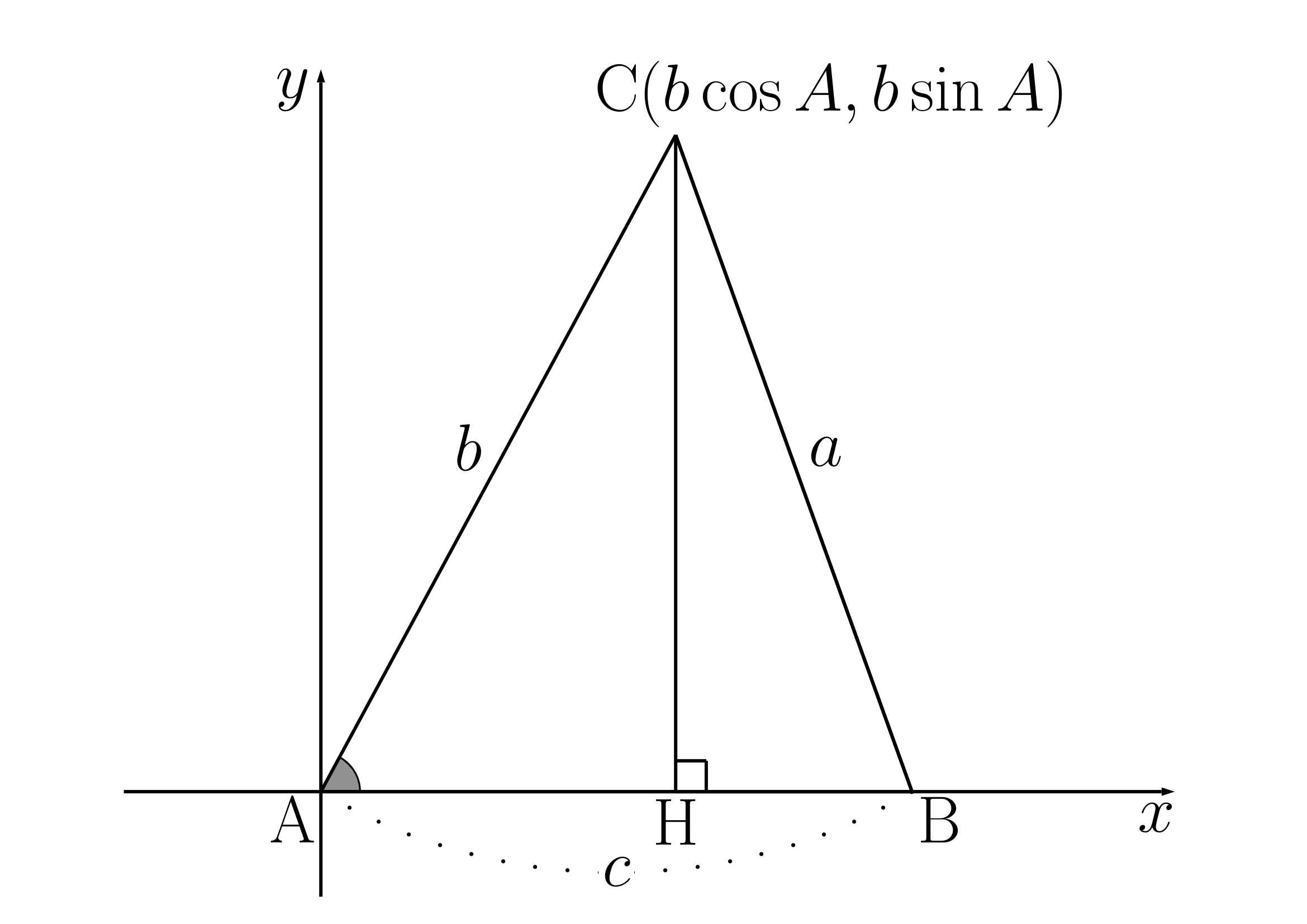
図のように原点が
この時
この時
よって以下が成り立ちます。
| + | より厳密な証明 |
よって
について以下が成り立つ。



また、これを変形した下の式も覚えておくとよいです。
について以下が成り立つ。



問題
 において、
において、
(1) の時、
の時、 を求めよ。
を求めよ。
| + | ... |
(2) の時、角
の時、角 を求めよ。
を求めよ。
| + | ... |
 において、外接円の半径を
において、外接円の半径を とする。
とする。
(1) の時、
の時、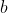 を求めよ。
を求めよ。
| + | ... |
(2) の時、角
の時、角 と
と を求めよ。
を求めよ。
| + | ... |
(3) の時、最も大きい角を求めよ。
の時、最も大きい角を求めよ。
| + | ... |
(4)) が成り立つとき、
が成り立つとき、 はどんな三角形か
はどんな三角形か