n番目の素数 - 数学 @ ウィキ

目次

素数

---

• 素数

自分自身と1でしか割り切れない数。

---

今まで、数々の数学者たちが素数の謎を追求してきた。
しかし、素数とは実に不思議な数だ。
その存在を理解するのはとても無理難題であった。
こんかいはそんな素数の謎に迫る。

存在の発見

素数とはいったいどのようにして発見されたのだろうか。
その発見には遠い昔までさかのぼる。
数を扱う最初の段階は、おそらく「数える」という行為から始まる。
例えば、物の個数を数えるという日常的な活動から、数字を使って物事を記録する方法が生まれた。
初期の文明（例えば古代エジプトやメソポタミア）では、数を記録するための記号やシステムが作られていった。
数の概念が確立されると、次に足し算や引き算が生まれた。
これは、物事を比較したり、合計を求めたり、逆に減らす必要が出てきたからだ。
足し算と引き算は、数の理解を深め、さまざまな計算に応用される基礎となった。
次に進んだのが掛け算と割り算である。
これは、物の集まりや分割の概念が重要になる中で自然に発展していった。
掛け算は、足し算の反復であることに気づいた人々が、それを効率よく表現するために生み出したものだ。
また、割り算は、物を等しく分ける必要が生じ、発明されていった。
このように、数の操作は基本的な算術から発展し、より複雑な数の関係を扱うためのツールとして、掛け算や割り算が確立されていった。
素数の概念は、数の操作がある程度確立した後に登場する。
素数とは、1と自分自身以外の約数を持たない数（例えば2, 3, 5, 7, 11など）である。
素数が「発見される」と言っても、実際には人々が数の性質を探求し、その中で「素数」と呼ばれる特別な数の存在に気づいていったのである。
素数が重要だと認識されるようになったのは、古代ギリシャの数学者エウクレイデス（ユークリッド）などが素数に関する理論を発展させた時期だ。
紀元前3世紀頃に古代ギリシアの大数学者ユークリッドが編纂(へんさん)したとされる数学書『原論』の中で、早くも「素数が無限に存在する」ことが証明されている。

無限の存在

では素数の知識を深めるため、素数が無限に存在することを証明してみる。
まず、こう仮定する。
「素数は無限にはなく、だけ存在する」
では次にという値を決める。
ここではのように、存在するすべての素数をかけた数に1を足したものとする。
この時以下のような性質がある。

• が素数の時

これは存在するすべての素数の素数のどれとも違う、新しい素数。

• が素数でないとき

これは存在するすべての素数のどれでも割り切れない。
つまり、を割り切れる新しい素数が存在する。

しかしそうすると、がどんな値でも、存在するすべての素数と異なる素数が存在することになる。
つまり、存在するすべての素数はではなく、もっと多くあるということになる。
しかし、素数を数を増やしてもう一度「有限個ある」とすると、同様の操作でさらなる素数が存在することが証明できる。
つまり、最初の仮定
「素数は無限にはなく、だけ存在する」
が間違っていたということである。
よって次のことがわかる

素数は無限に存在する。

素数が作る美しい階段

では次に素数階段という階段を上ってみよう。
素数階段とは次のような階段である。

1歩づつ進んでいき、素数の数だけ進むごとに段が一つ上がる。

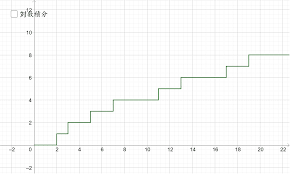
グラフに表すとyを階段の段数、xを歩数としたグラフである。
例えば、の地点で、6以下の素数はの3つあるのでである。
ちなみに素数階段ではグラフはで表される。
だ。
次に対数関数という関数についてみる。
対数関数とはのようにあらわされ、bはaを何回かけた数かを調べる関数である。
例:
  8は2を3回かけた数
  81は3を4回かけた数
そして、を使ったのグラフを見てみよう。
グラフはこのようになる

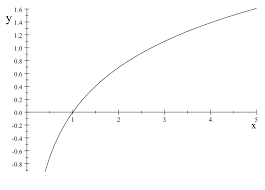
では、素数階段での時になる。
また、になる。

そして、これからになる。

168との差は約23.24、誤差としてはだ。

次にの時の素数階段のである。
そしてである。

また、だ

1229との差は約143.26、誤差としてはだ。

次にの時の素数階段のである。
そしてである。

また、だ

2262との差は約242.21、誤差としてはだ。

このようにはにちかづいている。
つまりだ。
※とはxを無限大みたいな大きい数で計算するという意味。

n番目の素数

では強引にn番目の素数を求めてみよう。

素数の性質

素数kについてのあまりは-1になることが知られています。
例:

※強引な書き方ですが、こういう表し方もあります。

これは合同式を使うと説明できます。

証明:合同式を習った人向け

を示す。
の時、
より成り立つ。
の時
整数a,bについて考える。
はすべてnで割った余りが異なる。
よってとなるbがに一つだけ存在する。
ただしnが素数でないとき、の中にnで割った余りが-1でない組み合わせが存在してしまう。
よってnは素数。
しかしの時、となり、である。
ここで合同式の性質からまたはである。
つまり、の時に限りでが成り立つ。
また、において、の中で、ペアを作るとこれらの積はnで割ると1余る。
よってである。
よって

つまり、はkで割り切れるということになります。
よってはkが素数の時のみ整数になります。

三角関数の持つ性質

一般にです。
ここからであります。
また、整数aについての時になります。
つまり、整数ではない数bについてとなります。
つまり、とすると、xが整数の時だけ1に、分数の時は0になるという関数ができました。
※とは、aの小数点以下を切り捨てるという操作です。
※例:
これを使い、とすると、xが素数の時1になる関数ができました。
※弧度法という角度の測り方を使うとになります。は「ラジアン」のことです。
そして、ある数nまでの素数の数を数えたいときは、とすればよいです。
※になるが、1は素数でないため-1しています。

ある数nまでの素数の数: