順序数(Ordinal Numbers)
概要
数学の特に集合論において、順序数(じゅんじょすう、英: ordinal number)とは、整列集合同士の“長さ”を比較するために、自然数を拡張させた概念である。By Wikipedia
簡単に言えば、
0、1、2、3、4、5...と続く(0と)自然数の先をさらに拡張した数。
0、1、2、3、4、5...と続く(0と)自然数の先をさらに拡張した数。
定義
整列集合 に対して、
に対して、 を定義域とする写像
を定義域とする写像  を超限帰納法によって
を超限帰納法によって

と定義したとき、 の値域
の値域 を
を の順序数といい、これを
の順序数といい、これを で表す。ある整列集合の順序数であるような集合を順序数と呼ぶ。
で表す。ある整列集合の順序数であるような集合を順序数と呼ぶ。
と定義したとき、
...ページ制作者すらなんて言ってるかわからないので、スルーするといいです。
自然数
順序数は自然数を拡張した概念なので、最初は自然数から始まります。




とこのように続いていきます。
とこのように続いていきます。
ところで、 で表せる順序数のことを、後続順序数と言います。
で表せる順序数のことを、後続順序数と言います。
なので、1、2、3、4、・・・は後続順序数です。
ところで一つ思いました。全ての自然数の次ってなんでしょう?これが順序数の幕開けなのです...
なので、1、2、3、4、・・・は後続順序数です。
ところで一つ思いました。全ての自然数の次ってなんでしょう?これが順序数の幕開けなのです...
最初の無限 ω
なので自然数よりでかいです。
そして、
とにかく
今までに出てきたやつで順序数は3つに分類できます。
| 分類 | 例 | 説明 |
| 最小の順序数 | ||
| 後続順序数 | n+1の形で書ける | |
| 極限順序数 | どの順序数の次でもない |
ところで、なんで はダメなのでしょうか?
はダメなのでしょうか?
計算
順序数の計算はとてもややこしいです。
足し算
順序数の足し算は、なんと非可換。
つまり左右を入れ替えると答えが変わってしまいます。

なんでこんなわかりづらい仕組みがあるのでしょうか。
順序数は順序が大切なので、「1個右に動いてから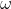 回右に動く」と「
回右に動く」と「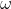 回右に動いてから1個右に動く」のは違います。
回右に動いてから1個右に動く」のは違います。
とにかく、「左に小さい数があったら吸収される」と覚えておきましょう。
つまり左右を入れ替えると答えが変わってしまいます。
なんでこんなわかりづらい仕組みがあるのでしょうか。
順序数は順序が大切なので、「1個右に動いてから
とにかく、「左に小さい数があったら吸収される」と覚えておきましょう。
引き算
順序数では、マイナスはないので、引き算はありません。
なので はありません。
はありません。
なので
掛け算
順序数の掛け算も非可換です。

ちなみに掛け算の記号に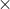 を使ってますが、
を使ってますが、 を使うことが多いです。(画面の汚れではありません、・です。)
を使うことが多いです。(画面の汚れではありません、・です。)
なのでここ以降は を使います。
を使います。
順序数の掛け算では、右分配法則は成り立ちますが左分配法則は成り立ちません。


ちなみに掛け算の記号に
なのでここ以降は
順序数の掛け算では、右分配法則は成り立ちますが左分配法則は成り立ちません。
割り算
順序数に割り算はありません。
べき乗
順序数のべき乗も非可換。

非可換なのは元からだな。
非可換なのは元からだな。
順序数でもまだ成り立つもの
- 結合法則
結合法則は数の順序を変えてないので成り立ちます。
- 単位元においての可換性
簡単に言えば、 で、
で、 ってこと。
ってこと。
- 指数法則
ωのその先
無限の先に、さらに無限がある。これが順序数の面白いところです。
さてこれを繰り返すと に到達します。
に到達します。

です。
もちろんこのまま
 、
、 、
、 、
、
としてもいいのですが、そんなのキリがないので掛け算に演算をレベルアップさせます。
 、
、 、
、 、
、 、
、
さらに繰り返すと になります。
になります。
ここで にします。
にします。
 、
、 、
、 、
、 、
、
すると までできます。
までできます。
 、
、 、
、 、
、
さてこれを繰り返すと
です。
もちろんこのまま
としてもいいのですが、そんなのキリがないので掛け算に演算をレベルアップさせます。
さらに繰り返すと
ここで
すると
さて、最後の列はめっちゃすごいのですが、これを超える列はあるのでしょうか?
あります。それがイプシロン数(エプシロン数)です。
あります。それがイプシロン数(エプシロン数)です。
イプシロン数(ε数)
先ほど出てきた  のような連鎖の限界を考えてみましょう。
のような連鎖の限界を考えてみましょう。
この「どこまでも続く冪の列」の極限が、 (イプシロン・ゼロ)です。
(イプシロン・ゼロ)です。
では、どういう数か?
つまり、「自分自身を冪にしても変わらない」最初の順序数です。
一般に、 を満たす順序数
を満たす順序数 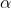 を、イプシロン数(ε数)といいます。
を、イプシロン数(ε数)といいます。
最初のイプシロン数が  、その次が
、その次が  、その次が
、その次が 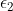 ... と続いていきます。
... と続いていきます。
もちろんこれにも先があります。
このような列を考えてみましょう。
このような列を考えてみましょう。
もちろんこの先は ですが、そこからずっと進めるのはめんどくさいので
ですが、そこからずっと進めるのはめんどくさいので まで一気に進めます。
まで一気に進めます。
そしてこの列の果てってなんでしょう?
ゼータ数です。
ゼータ数です。
ゼータ数
ゼータ数は、 な数です。
な数です。
つまり、「イプシロン数の添字にしても変わらない数」です。
最初のゼータ数が 。そして
。そして 、
、 、
、 、
、 と続いていきます。
と続いていきます。
つまり、「イプシロン数の添字にしても変わらない数」です。
最初のゼータ数が
ヴェブレン階層(Veblen hierarchy)
今まで出てきた順序数は、
 、
、
のように「不動点」を使って新しい数を作ってきました。
のように「不動点」を使って新しい数を作ってきました。
「不動点」とは、関数をかけても変わらない点のことです。
たとえば、 を満たす
を満たす 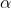 が
が  でした。
でした。
たとえば、
では、「不動点をどんどん生成する関数」を階層的に定義していくとどうなるでしょうか?
これが ヴェブレン階層 です。
これが ヴェブレン階層 です。
定義
ヴェブレン階層  ) は次のように定義されます。
) は次のように定義されます。
-
-
) = 「
の不動点のうち、
番目のもの」
-
) = 「すべての
に対して定義された
の共通不動点のうち、
番目のもの」
……と、文章で読むとやばい感じがしますが、順番に見ていきましょう。
例
| 段階 | 関数 | 説明 |
| 普通のべき乗 | ||
| 冪の不動点(イプシロン数) | ||
| イプシロン関数の不動点 | ||
| ゼータ関数の不動点 | ||
そしてこの階層をどんどん続けていくと、
「どの階層にも属さないほど巨大な不動点」が現れます。
「どの階層にも属さないほど巨大な不動点」が現れます。
フェファーマン=シュッテの順序数(Γ₀)
ヴェブレン階層を使うと、

を満たす最小の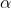
が存在します。
を満たす最小の
が存在します。
それが  です。
です。
つまり、Γ₀は
「ヴェブレン階層そのものの最初の不動点」なのです。
「ヴェブレン階層そのものの最初の不動点」なのです。
解説
Γ₀は、ここまでに出てきた
 や
や 
をすべて内包するレベルの“超・自己再帰的”な無限です。
をすべて内包するレベルの“超・自己再帰的”な無限です。
なので Γ₀ は「Feferman–Schütte ordinal」と呼ばれ、
論理学では「直観主義的解析の限界」として登場します。
論理学では「直観主義的解析の限界」として登場します。
ちなみにここまでとてもデカい順序数が出てきたが、
その順序数が対応する基数はまだまだ である。
である。
その順序数が対応する基数はまだまだ
ψ関数
ψ関数は順序数崩壊関数で、なんかめっちゃ大きい順序数を出せるが、ページ制作者すら何かよくわかってないため、詳しくは書けない。
誰か続き書いてくれー
誰か続き書いてくれー
非可算順序数(ω₁)
ここまでに登場した順序数(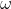 、
、 、
、 など)は、すべて可算でした。
など)は、すべて可算でした。
つまり、自然数と一対一対応が取れる範囲の“数えられる無限”です。
どれほど大きな順序数でも、有限な手順で名前をつけられる間は「可算」です。
つまり、自然数と一対一対応が取れる範囲の“数えられる無限”です。
どれほど大きな順序数でも、有限な手順で名前をつけられる間は「可算」です。
しかし、順序数の世界にはそれを超える“数えられない無限”が存在します。
その最初のものが、 (オメガ・ワン)です。
(オメガ・ワン)です。
その最初のものが、
定義
 は「すべての可算順序数の集合の順序型」です。
は「すべての可算順序数の集合の順序型」です。
つまり、これまでに出てきたすべての順序数(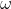 、
、 、
、 など)をひとまとめにして並べたときの“その次”が
など)をひとまとめにして並べたときの“その次”が  です。
です。
つまり、これまでに出てきたすべての順序数(
この定義から、 自身は非可算になります。
自身は非可算になります。
なぜなら、“可算なものをすべて並べても”その全体は可算ではあり得ないからです。
なぜなら、“可算なものをすべて並べても”その全体は可算ではあり得ないからです。
そして、 は2番目の正規順序数です。
は2番目の正規順序数です。
正規順序数とは、その数より小さい数をいくら足しても、その数には届かないという順序数のことです。
そして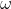 は最初の正規順序数です。
は最初の正規順序数です。
正規順序数とは、その数より小さい数をいくら足しても、その数には届かないという順序数のことです。
そして
性質
| 性質 | 説明 |
| 最小の非可算順序数 | これより小さい順序数はすべて可算 |
| 正則順序数 | |
| 基数としては |
最初の非可算基数 |
イメージ
可算順序数たち(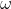 、
、 、
、 、
、 、
、 )をすべて積み上げても、
)をすべて積み上げても、
可算順序数たち(
それらを数え上げられる順序数はまだ「可算」です。
しかし、その全体の“次”を考えると、それはもはや「数えられない」——それが 。
。
しかし、その全体の“次”を考えると、それはもはや「数えられない」——それが
図で表すと
| レベル | 代表順序数 | 説明 |
| 有限 | 有限の範囲 | |
| 可算(第1の無限) | 自然数の列の先 | |
| 可算の階層構造 | 無限の上の無限 | |
| 非可算の始まり | “可算の果て”のその先 |
つまり、 は「可算で理解できる数学」と「それを超える数学」の境界線。
は「可算で理解できる数学」と「それを超える数学」の境界線。
ここを越えると、“無限の中の無限”の世界——基数論——が始まります。
なので続きは基数のページができてからにしましょう。
ここを越えると、“無限の中の無限”の世界——基数論——が始まります。
なので続きは基数のページができてからにしましょう。
おまけ: のその先
のその先
もちろん、 にも「次」があります。
にも「次」があります。
それが 、
、 、
、 と続いていきます。
と続いていきます。
もちろん、
それが
これらは基数としては
 、
、 、
、 、
、
と呼ばれます。
無限の階段はここでも終わりません。
それぞれの“無限”の先に、さらに大きな無限があるのです。By ChatGPT
