2次方程式の解の配置問題(基本) - 数学 @ ウィキ

2次方程式の解の配置

など2次方程式の解の場所が限定された問題をときます。
2次関数分野の終盤に待ち構える問題で、苦手としている人が多い印象です。
それなりに難易度が高いですが教科書範囲です。
大学入試で頻出です。

例題

xについての2次方程式が次の条件を満たすようなaの値の範囲を求めよ。
(1)異なる2つの実数解がともに2より大きい。
(2)正と負の解が1つずつある。
(3)2つの実数解がともににある。

問題の解き方

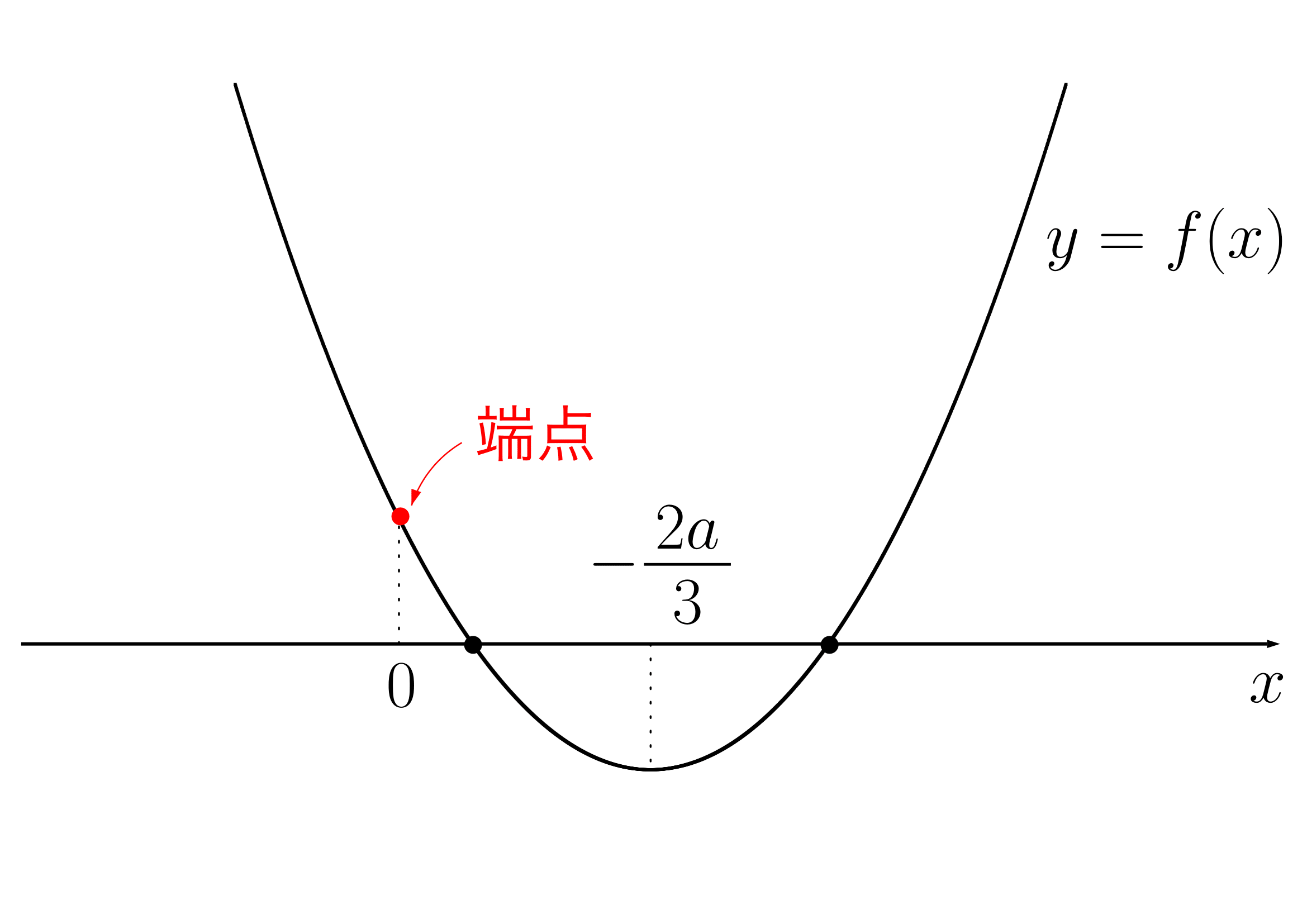
グラフを書いて(y軸は書かない)、3つの条件

• 端点条件(端点のy座標を図から判断)
• 軸条件(軸の範囲を図から判断)
• 判別式(またはか判断。(頂点のy座標で判断してもOK)

をチェック。
これらすべてを満たした共通範囲が答えです。
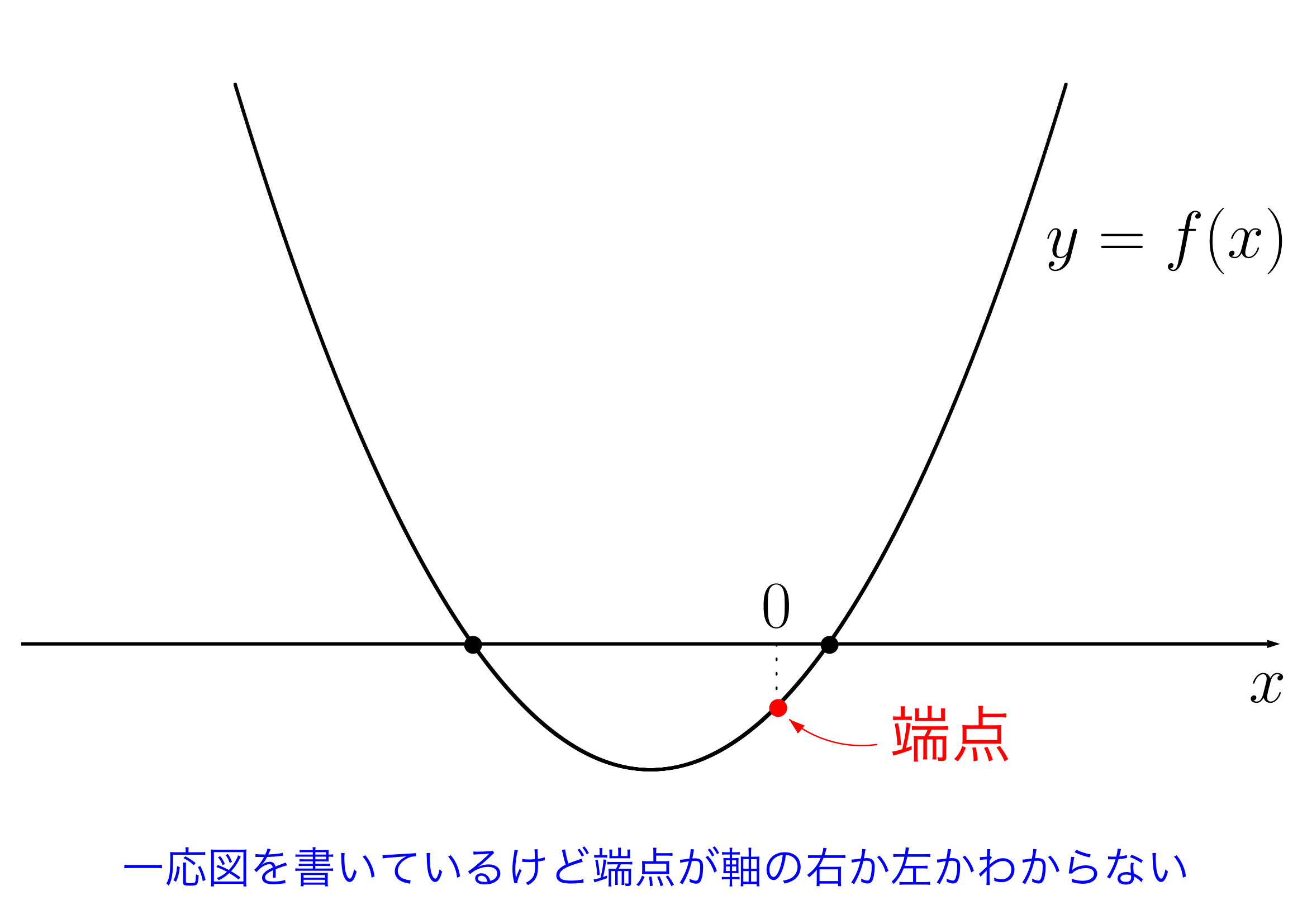
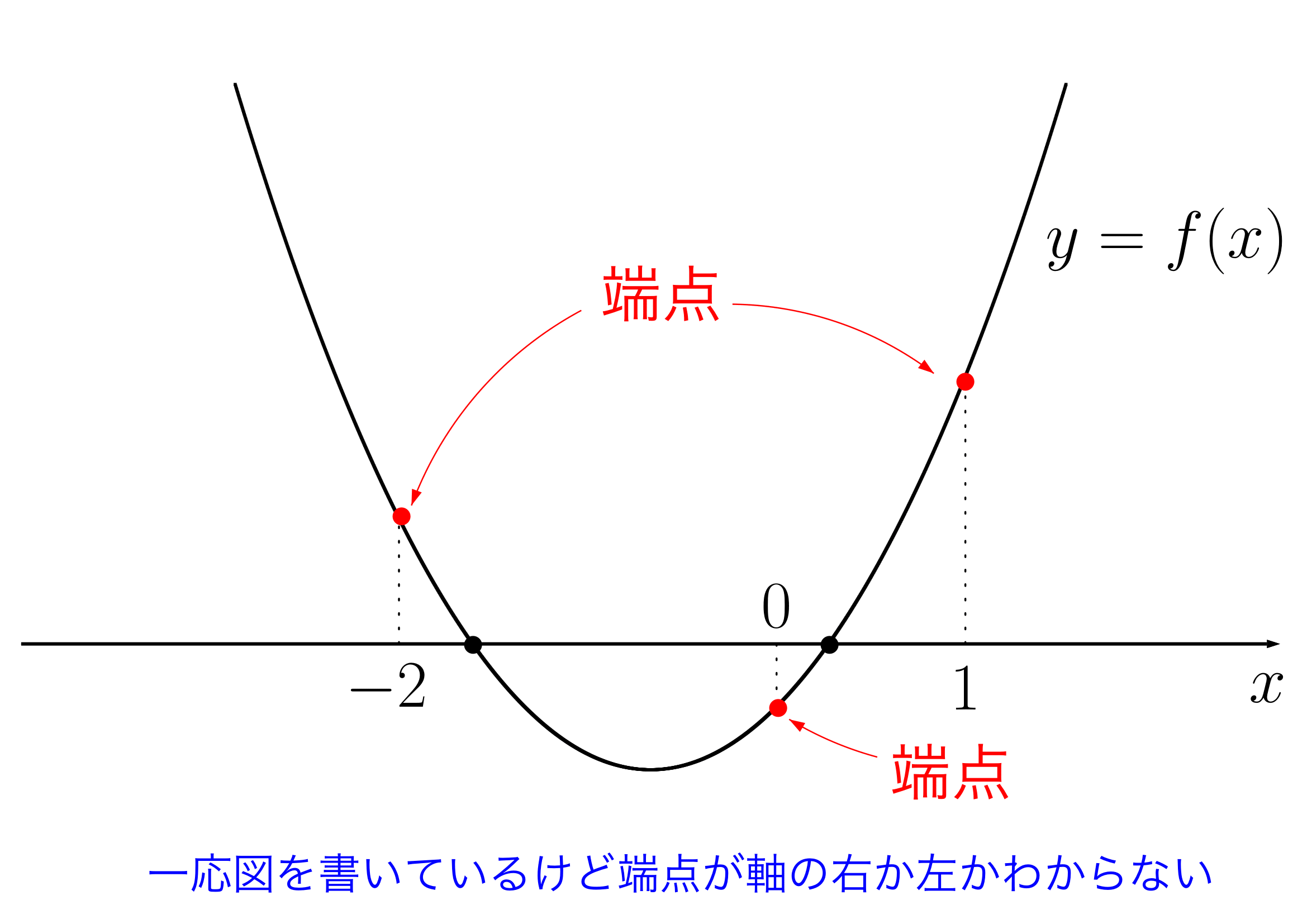
※端点とは、xの範囲の端にある上の点です。端点という用語は数学の正式な用語ではなく、解の配置問題を解くための便宜的な名前です。
例題で説明します。

解答と解説

とする。
この時、の軸はである。
※の軸はを利用。
(1)の実数解が2より大きい時のグラフは

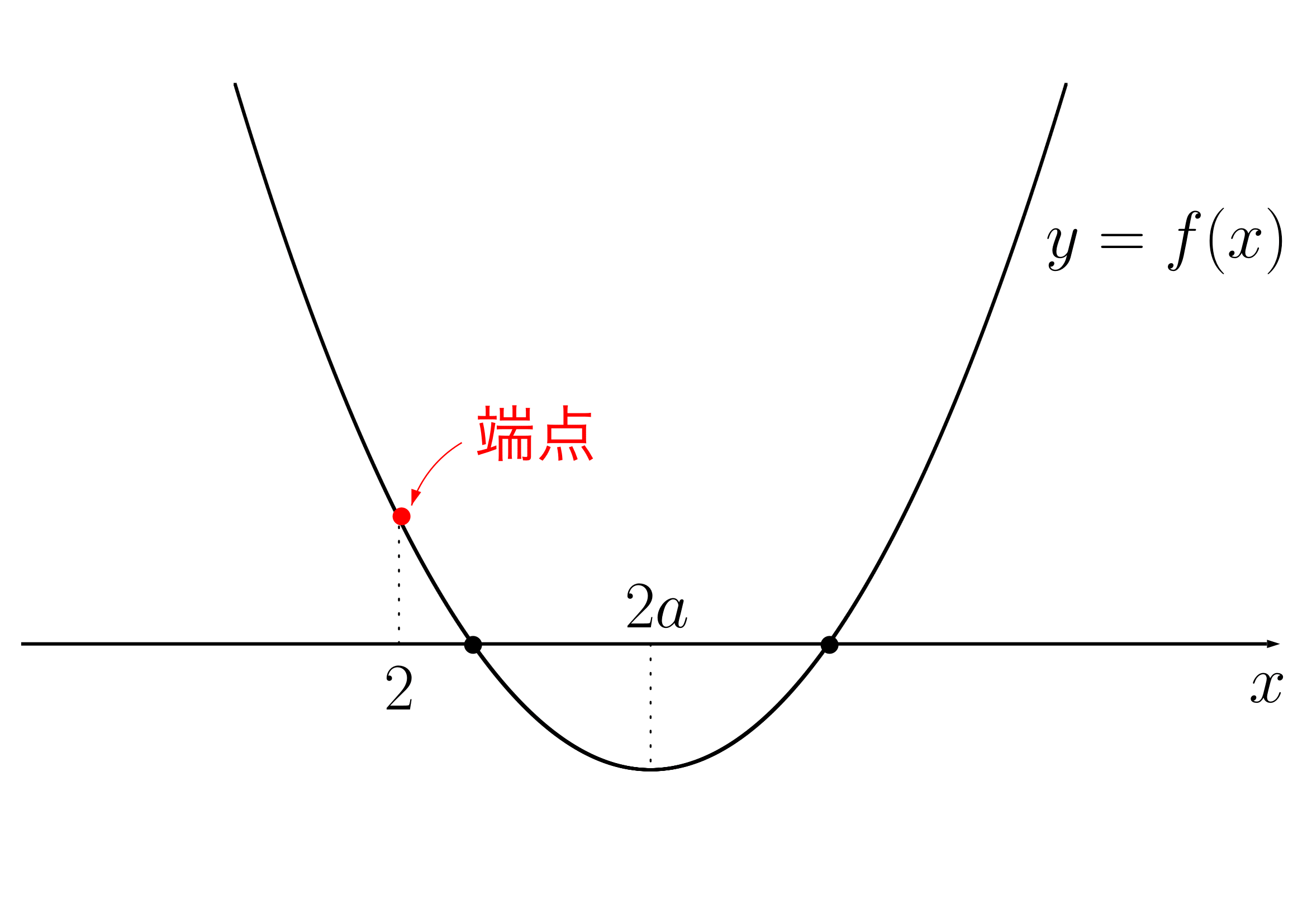
端点のy座標をチェックします。
図から明らかに正ですね。
つまり

• 端点条件：

次に軸条件です。
図から明らかですね。

• 軸条件：

最後に判別式です。
異なる2つの実数解をもつので

• 判別式：

これらの共通範囲より　

問題

xについての2次方程式が次のような条件を満たすaの範囲をそれぞれ求めよ。

...

とする。

(1)異なる2つの実数解がともに正である。

...

の頂点がにあればよく、かつであればよい。

よって
また、



そして
これらから

(2)正と負の解が一つずつある。

...

図としては

のように、であればよい。
よって

(3)それぞれに一つずつ実数解が存在する。

...

かつであればよい。

よって
また、
そして、
これらから