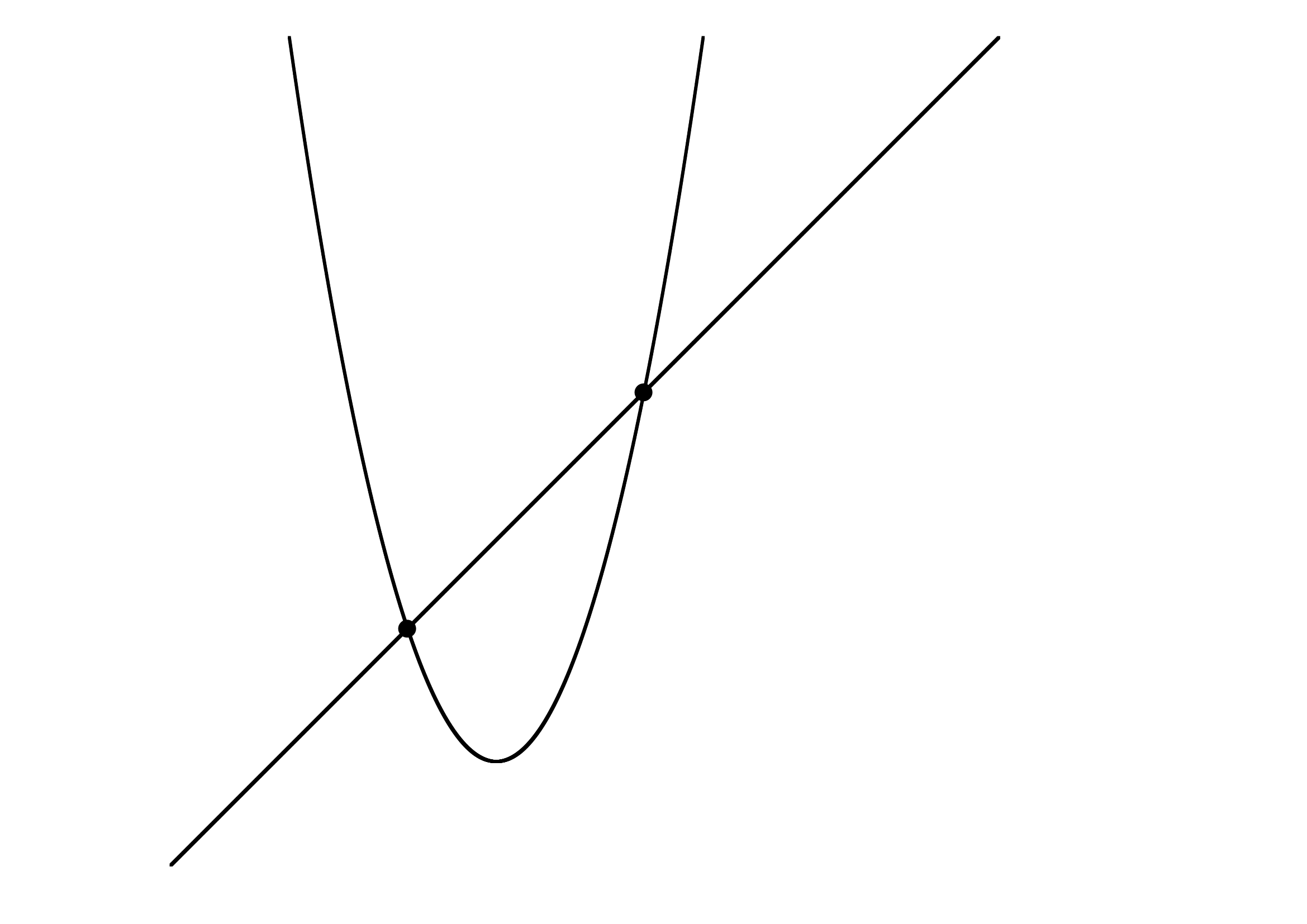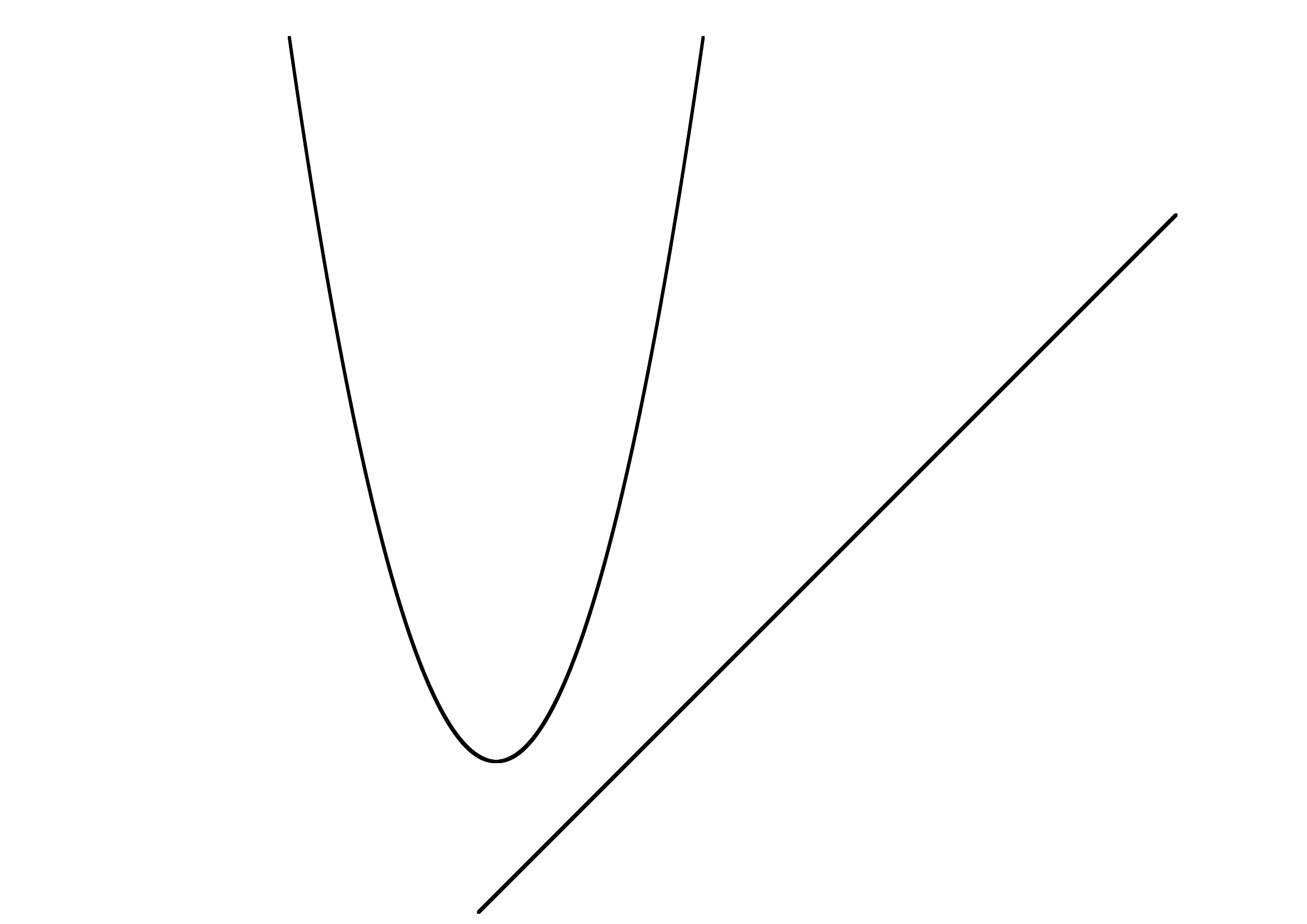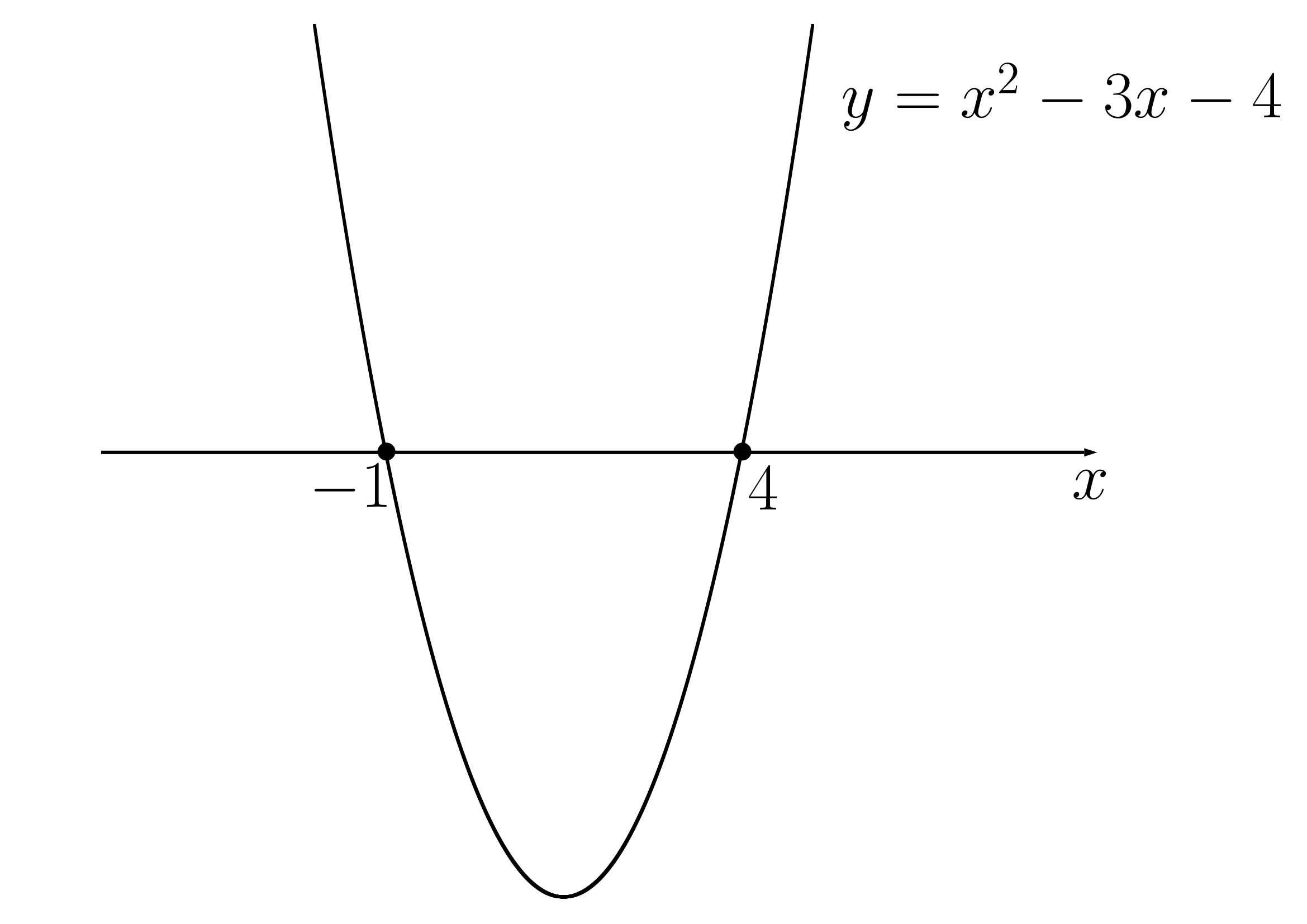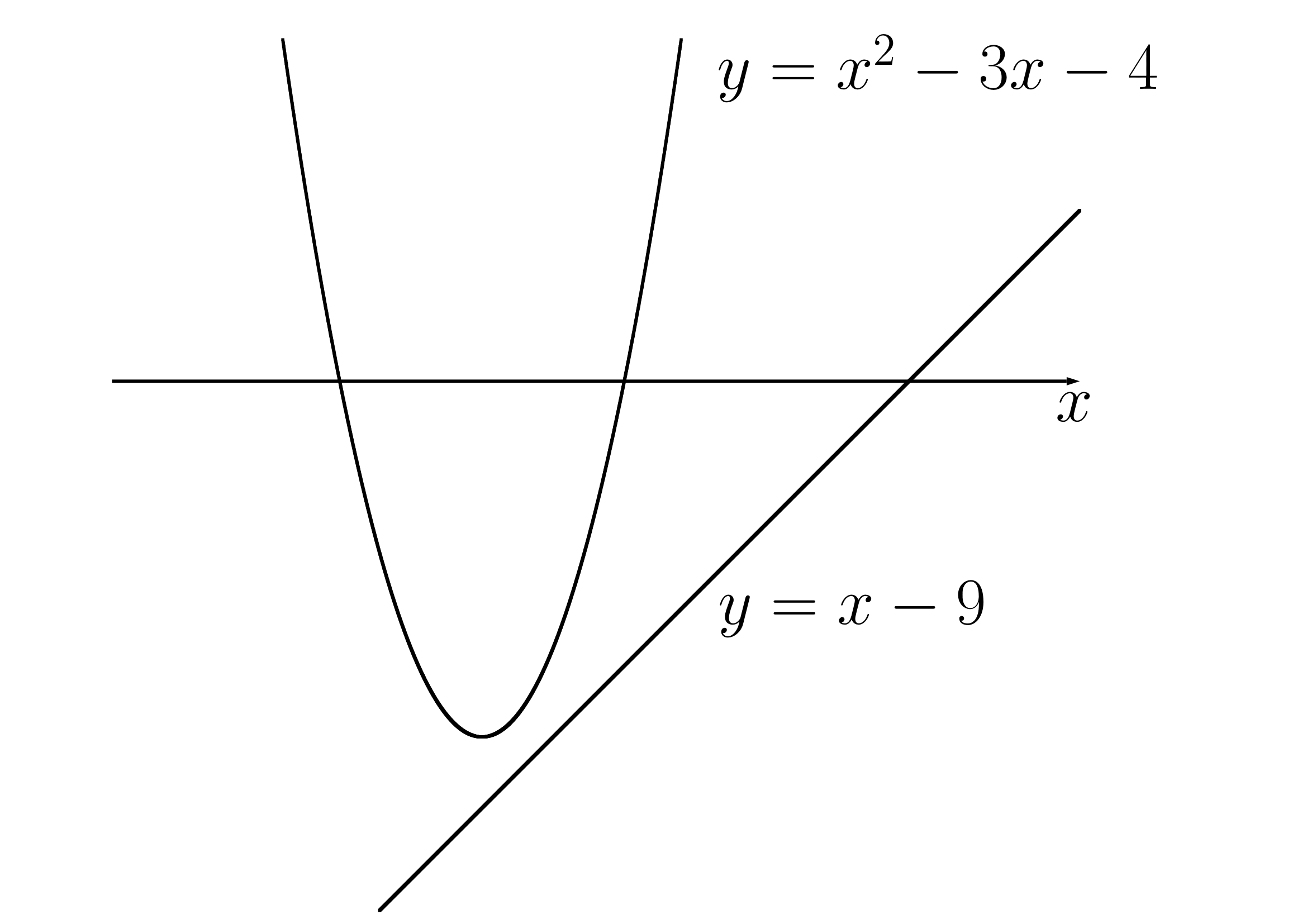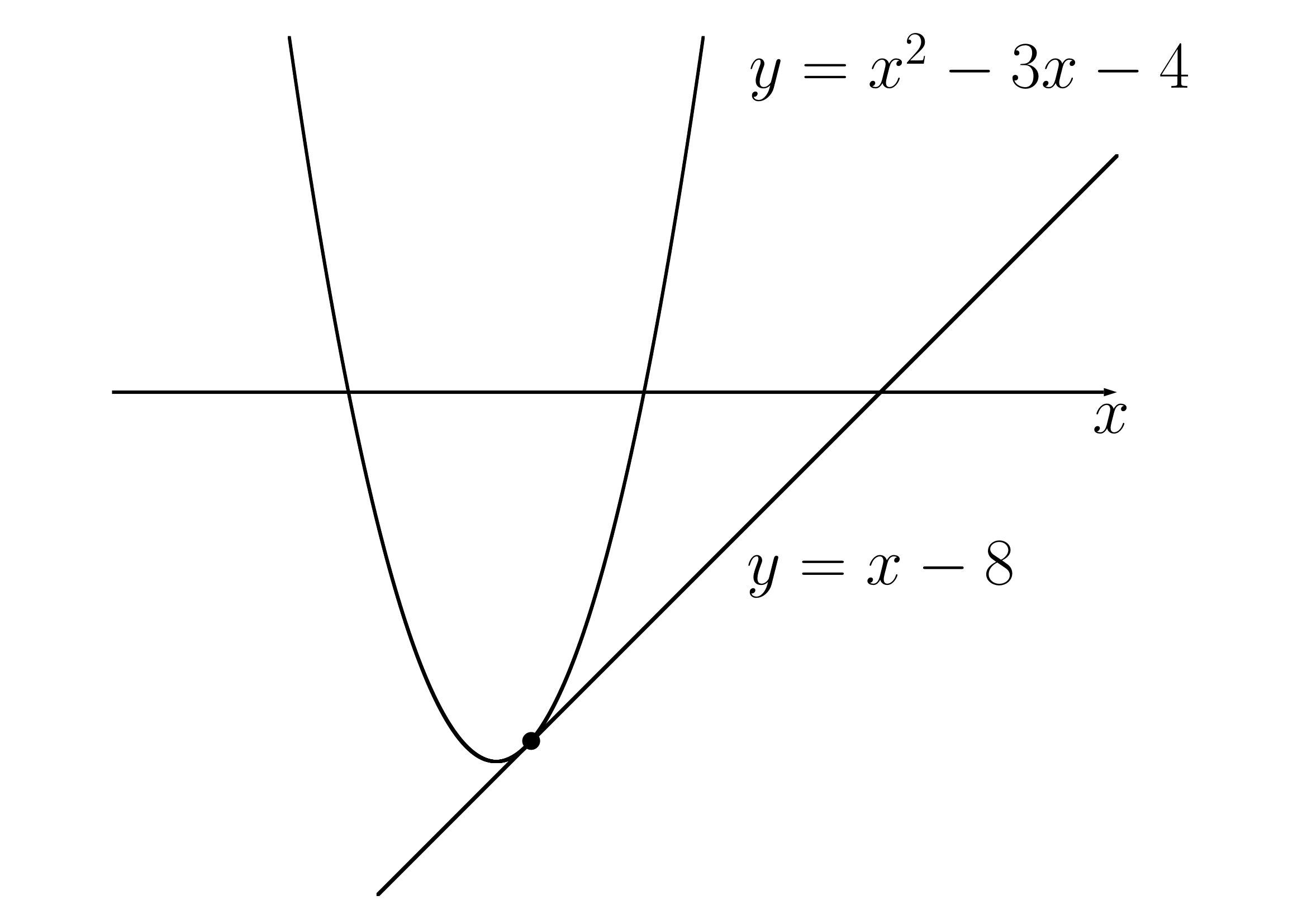共有点
判別式を利用し放物線と直線(x軸を含む)の共有点の個数や座標について扱います。
※共有点とはある関数のグラフと別の関数のグラフが重なった点のことです。
※共有点とはある関数のグラフと別の関数のグラフが重なった点のことです。
放物線とx軸の共有点
中学校で、2つのグラフの共有点の座標を求めるときは、2つのグラフを連立して方程式を解けばいいと習ったと思います。
それを利用し放物線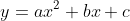 とx軸の共有点の座標を求めるときは、x軸は
とx軸の共有点の座標を求めるときは、x軸は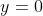 で表されるので、
で表されるので、

AをBに代入して、

この2次方程式を考えればいいです。
実数解が(共有点が)あるかどうかは判別式に従えばいいですね。
それを利用し放物線
AをBに代入して、
この2次方程式を考えればいいです。
実数解が(共有点が)あるかどうかは判別式に従えばいいですね。
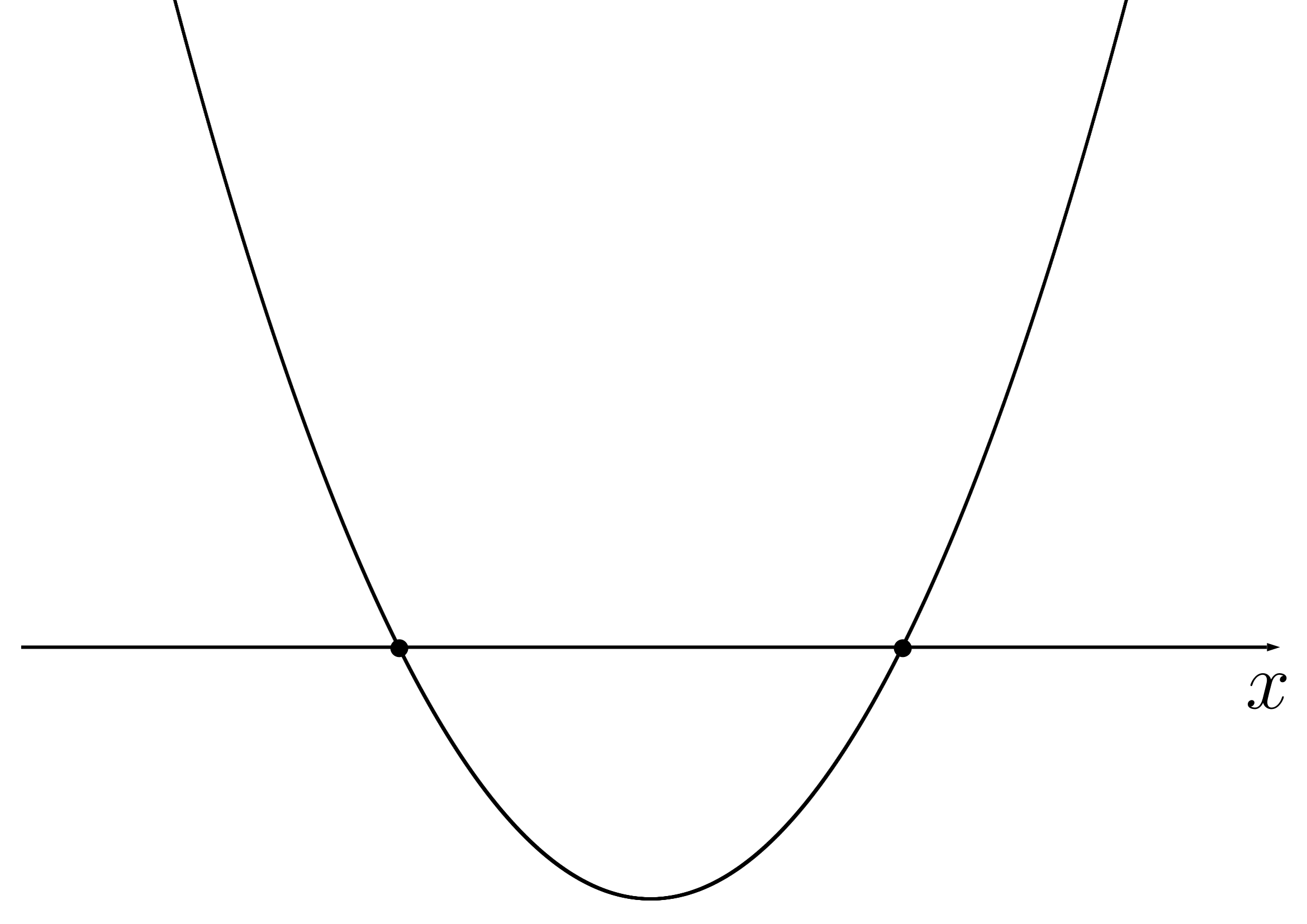
放物線とx軸の共有点の個数は、2次方程式
の判別式Dの値によって以下のように分類できる。
のとき共有点2個(異なる2点で交わる)
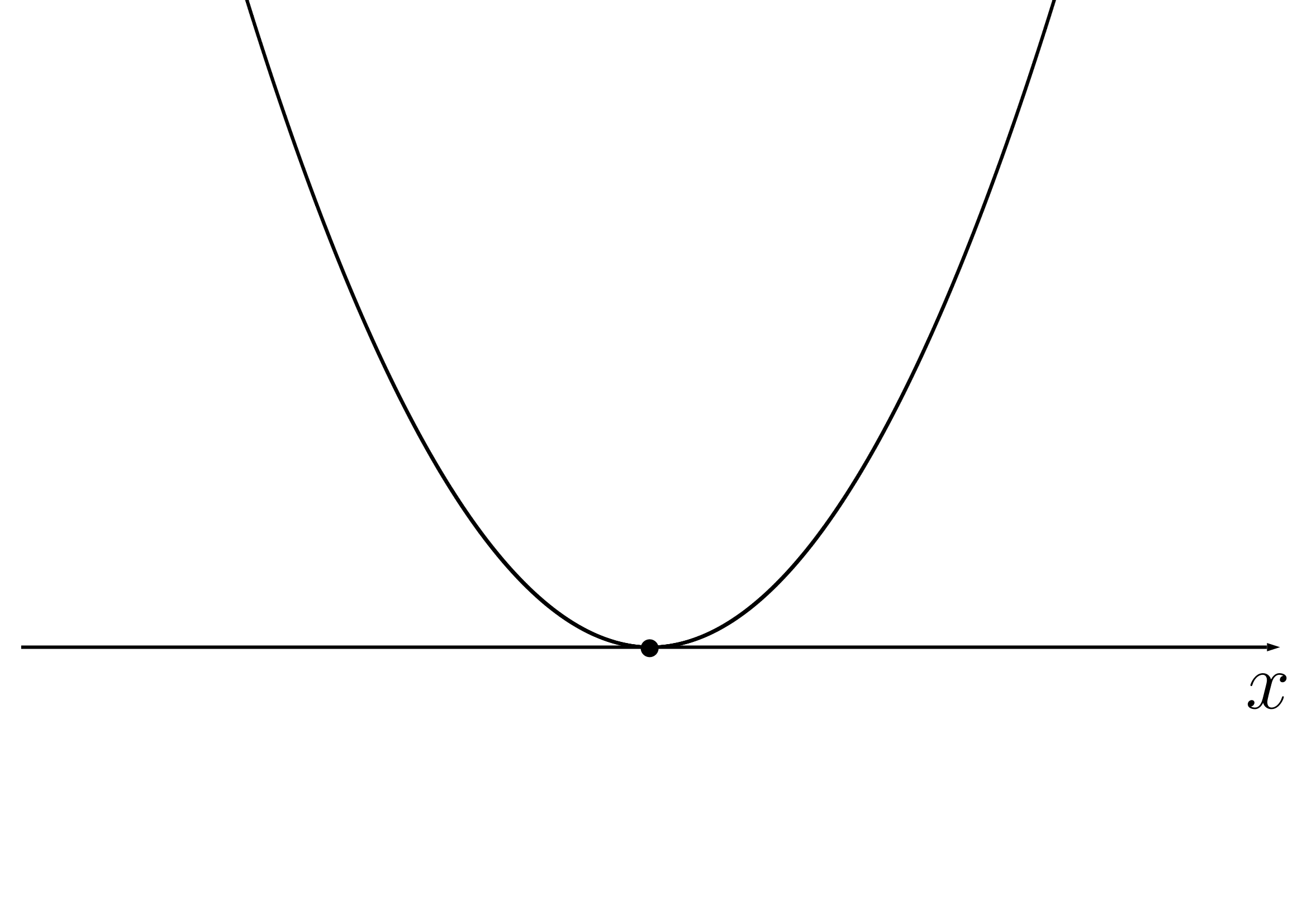
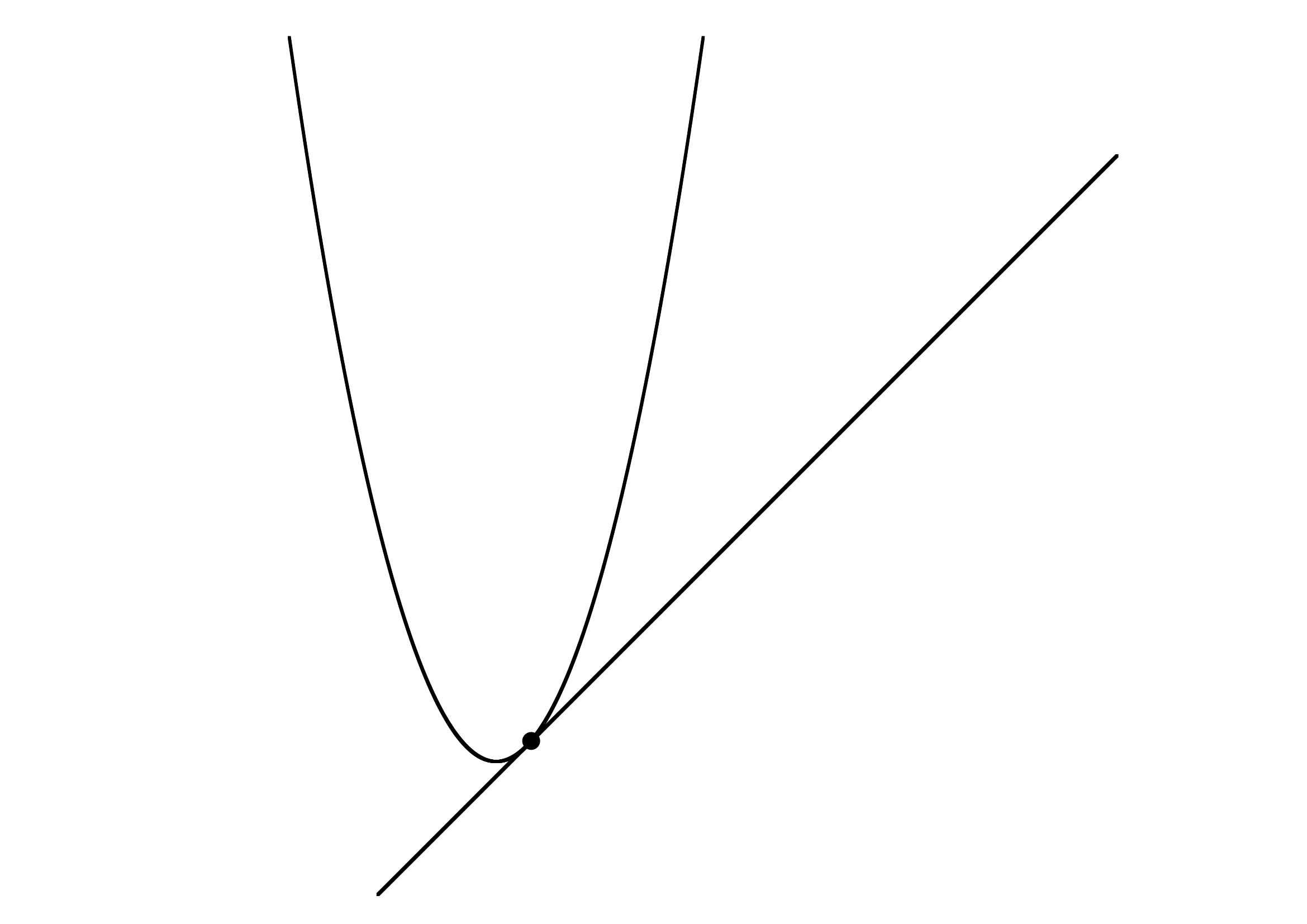
のとき共有点1個(x軸と接する)
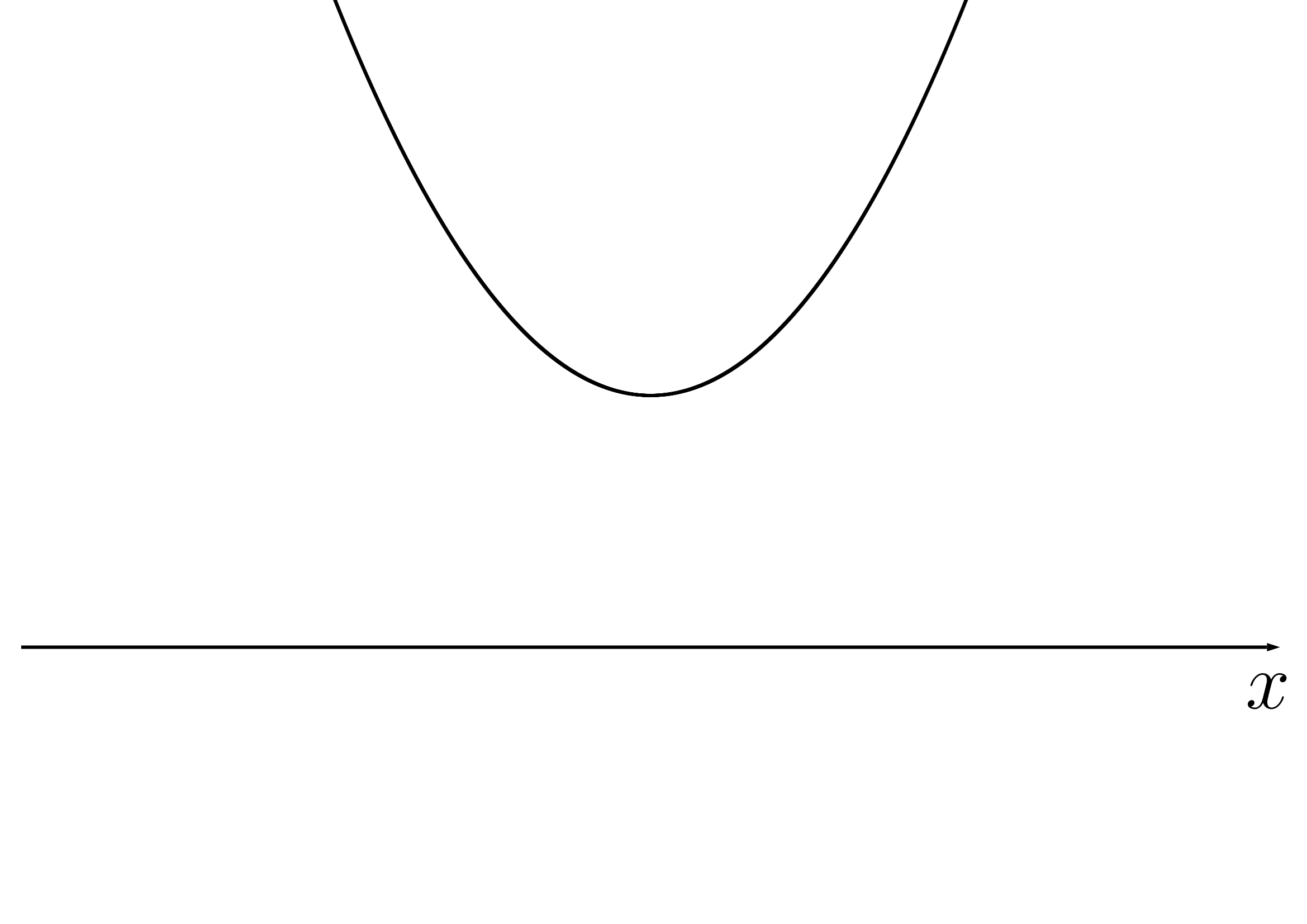
のとき共有点なし(交わらない)
※上の図は のときですが、
のときですが、 のときも同じです。
のときも同じです。
放物線と直線の共有点
x軸の時同様、 と
と の共有点の座標を求めるときはこれらを連立します。
の共有点の座標を求めるときはこれらを連立します。

AをBに代入して


この2次方程式を考えればいいです。
実数解(共有点)があるかどうかは判別式に従えばいいですね。
AをBに代入して
この2次方程式を考えればいいです。
実数解(共有点)があるかどうかは判別式に従えばいいですね。
放物線と
の共有点の個数は、2次方程式
の判別式Dの値によって以下のように分類できる。
のとき共有点2個(異なる2点で交わる)
のとき共有点1個(x軸と接する)
のとき共有点なし(交わらない)
問題
(1)放物線 とx軸の共有点の個数を求め、共有点があればその座標を求めよ。
とx軸の共有点の個数を求め、共有点があればその座標を求めよ。
| + | ... |
(2)放物線 と直線
と直線 の共有点の個数を求め、共有点があればその座標を求めよ。
の共有点の個数を求め、共有点があればその座標を求めよ。
| + | ... |
(3)放物線 とx軸が2点で交わるような定数kの範囲を求めよ。
とx軸が2点で交わるような定数kの範囲を求めよ。
| + | ... |
(4)放物線 と直線
と直線 が接するような定数kの範囲を求めよ。
が接するような定数kの範囲を求めよ。
| + | ... |