分散と標準偏差 - 数学 @ ウィキ

概要

高校のデータの分析や統計学で扱う分散と標準偏差について扱います。
数列のシグマ表記を使用しますので見方がわからない人は参照してください。

分散と標準偏差

分散

ある高校の定期試験で、数学と家庭科の平均点がどちらも70点だったとします。
この時数学はかなり点が低い人と高い人が混在し、家庭科では皆平均点付近に集中している可能性があります。
このよう平均値という情報から2つの試験はどちらも同じような試験だったと判定することはできません。
この場合2つの試験では散らばり具合が異なります。
散らばりの大きさの指標があると図にしなくてもわかるので便利です。
そこで分散というものが使われます。

まず、それぞれのデータと平均値の差を求めます。
次にこれらの平均値を求めてみましょう。

あるデータの平均値との差はで求めるとよいでしょう。

では、これらの平均値は

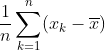
ここでは定数ですから

になってしまいます。
これでは情報を得ることができません。
ここでなぜただの引き算だと平均が0になるかというと、が負の数になることがあるからです。
そこで、平均値とデータの差を2乗します。
それらの和の平均値こそが分散でまたはで表します。

また、

ここでとすると、

よって

平均偏差

分散では2乗することで数を正の数に統一していましたが、2乗すると平均値から遠く離れた値との差が大きく開いてしまいます。
そこで絶対値をとったものを平均偏差といいます。

平均偏差=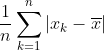

標準偏差

分散だと2乗しているので例えば身長のデータはで表されますが、分散はになってしまいます。
そこで分散の平方根をとることで単位をなどにそろえたものを標準偏差といます。

標準偏差：

問題

次のデータは英語の10点満点の小テストのとの2クラスの結果である。との結果をそれぞれとする。

x	2	2	4	8	9
y	0	2	6	7	9

(1)のデータの平均値をそれぞれ求めよ。

...

(2)のデータの分散をそれぞれ求めよ。

...

(3)のデータの標準偏差をそれぞれ求めよ。

...

(4))のデータについて標準偏差から平均値からの散らばりの度合いを比較せよ。

...

次のデータは英語の10点満点の小テストのとの2クラスの結果である。との結果をそれぞれとする。

x	4	5	6	7	8
y	0	1	9	10	10

(1)のデータの平均値をそれぞれ求めよ。

...

(2)のデータの分散をそれぞれ求めよ。

...

(3)のデータの標準偏差をそれぞれ求めよ。

...

(4))のデータについて標準偏差から平均値からの散らばりの度合いを比較せよ。

...