ビッグバンについて説明するためには一般性相対性理論についてまず理解する必要がある。ここでは難しい計算は省略し、導出に必要な知識とその結果だけを淡々と示していく。
1.特殊性相対性理論
宇宙の始まりを考える上で必要な一般性相対性理論を理解するために必要な基礎的な知識である。
特殊相対論では、空間内のすべての場所で、同じ運動力学が適用されるという仮説に立つ。この場合、ローレンツ変換と空間の回転という回転のみが扱われることになる。これらは、空間の歪みを表す「計量」のテンソルである計量テンソルを変えない。
一方で、一般相対論では、任意の座標変換を扱う。計量テンソルを重力エネルギーと仮定して扱う。
相対性理論の基本原理
動いている物体から光を見ても、光の速度は常に一定である。
このことから、時間は光の速さによって定義されることがわかる。
ここで、時間をtの代わりに、距離の単位wであらわすことにする。
つまり、w=ctが成り立つことになる。
ローレンツ変換
2つの慣性系の間の座標(時間座標と空間座標)を結びつける線形変換である。
簡単に言うと次のことである。「慣性の法則」が成り立つ空間である慣性系において、物質の速度が速くなればその分、物体の長さは縮む。しかし物体が縮むということは空間と時間も同じく縮むということである。
それを、静止系

と、x軸方向へ速度vで運動している慣性系

を想定した時に、具体的に数式化したものがローレンツ変換である。
t=0の瞬間、静止系K系の原点から光が放たれたとするとこの光は全方向に飛び去って、t秒後には原点から半径ctだけ離れた球面上の点に分布するはずである。これは下の式で表せる。

一方、慣性系K'系の原点にいる観測者から見ても、光は自分を中心に同心円状に広がるように見える。そのため、下の式が成り立つ。

今、K'系はX軸方向にまっすぐ動いているのだから、y軸やz軸方向に変化はない。このことに留意して計算すると、次の式が導出される。
この式は冗長で扱いにくいので、


と定義すると、


とすっきりした形であらわすことができる。
4元速度
上で示した4次元空間に対する物体の速度である。
つまり、時間軸、X軸、Y軸、Z軸のことである。
以下のように定義する。
ミンコフスキー空間
上で示したローレンツ変換の式から、次のことが分かる。
ローレンツ変換を行っても、次の恒等式が成り立つ。これが重要である。

この空間のことをミンコフスキー空間と呼ぶ。
このとき、以上のことから、ローレンツ変換前後の微小変化を

と表現すると、以下の式が常に成り立つ。

これらを

で割ると速度になるわけだから、

が成り立つことがわかる。
ここで、

であることを利用する。

で割って変形していくと、

であるため、以下のようになる。

4元運動量
運動量はpであらわされるが、これを4次速度で4元速度で示した4次元方向に拡張すると、

となる。このとき、それぞれの運動量は次のように表せる。

今、4元運動量についてγを使って書き改めると、

となる。つまり

である。
このとき、

の式に

を両辺掛け合わせると、

となることがわかる。
ここで、定義を考えると、

というのは、時間軸を除いた3次元空間の運動量なのだから、それぞれ、

と置き換えても何ら問題はない。
そこで、この空間方向の3次元の運動量をまとめて

とすると、

という形になる。
ここで、運動エネルギーの式は

である。
これが意味するのは、先ほど導出した近似式の両辺にcをかけると、エネルギーの式になるということである。

となる。よってこれがエネルギーの式となることがわかる。
ここで初めて、

の正体が、物質の持つ全エネルギーEをcで割ったものだったことがわかった。
さて、近似式を用いる直前の式に戻ってみる。
今、

に

を両辺かけると、

となる。もし運動量がゼロならば、

なので、かの有名な式が遂に姿を現す。

である。
逆に、運動量が存在する場合、

なのだから、



よって、

となる。
2.線形代数
ここで、話題を一度、数学に変える。一般性相対性理論を理解するために必要な線形代数(ベクトルや行列を含む概念)の知識なので説明していく。
共変ベクトルと反変ベクトル
最初の座標の基底ベクトルを

、新しい座標の基底ベクトルを

としたとき、次のように書ける。



これを

として省略すると以下のように表せる。

これをさらに省略すると以下のようになる。これをアインシュタインの縮約という。

...(*)
物理学的に説明すると、最初の座標の基底ベクトルを

、新しい座標の基底ベクトルを

としたとき、速度ベクトルの形の式で成分の変換が行われるものを反変ベクトルと呼び、逆に勾配ベクトルの形で成分の変換が行われるものを共変ベクトルという。
したがって、定義上、速度ベクトルは反変ベクトル(添え字が上付き)だということになる。
テンソル
古典的なアプローチではテンソルは多次元の配列の総称である。これで理解することは困難であるため、具体的に低次元の場合の例を示す。
- 階数0のテンソル:スカラー
- 階数1のテンソル:ベクトル
- 階数2のテンソル:行列
このように階数nの配列をまとめて示す概念がテンソルなのである。
上記で示したものは反変ベクトルだが、これは言い換えれば1階の反変テンソルということである。行列の形をとったものは2階の反変テンソルとなり、これから説明するエネルギー運動性テンソルTがまさにそれに該当する。
エネルギー運動性テンソルTμν
質量mの物質を考える場合、エネルギーや運動量は、

と見えることが、特殊性相対性理論の議論でわかっている。
これを4元速度であらわすと、

となる。
質量がふわーっと広がって存在する場合、つまり質量が連続した密度分布を持っている場合、密度ρの連続体であるのだから、

となる。
この状態についてよく考えると、連続体は進行方向に対して縮んでいるように見えるため、体積が縮んだ分だけ、単位面積当たりの密度はγ倍に増加しているように見えることになる。これは運動量密度πにも当然あてはまる。したがって、以下の式が成り立つ。
これをエネルギー運動量テンソルと呼ぶ。この行列は 2つの4元速度の組み合わせで出来ているので、速度ベクトルは反変ベクトルなのだから、エネルギー運動量テンソルは当然、2階の反変テンソルとして変換される。
3.一般相対性理論の2つの重要な式
一つは測地線の方程式である。
測地線の方程式は、光を含めたあらゆる物体が4次元空間の中でたどる道筋を表している。物体は光を含めすべて、曲がった4次元空間の中をまっすぐに進んでいるのである。測地線というのは「直線」のことである。
Γ記号は「クリストッフェル記号」と呼ばれており、略記号である。空間の歪みを表す「計量」という量の組み合わせで出来ている。
もう一つの式は重力場の方程式(別名:アインシュタイン方程式)である。
右辺に出てくる

は定数である。このGは古典論にも出てくる重力定数であり、cは光速度を表している。しかしこの

は、空間の曲がり具合を表す量「計量」が非常に複雑に組み合わさったものである。
測地線の方程式
λ、μ、νはそれぞれ0から3までの添え字である。したがって、完全に展開すると、その組み合わせは、4×4×4=64通りである。全て展開するとき、その項の数は、λを固定した場合に1+4×4=17項なので、λを動かした場合は17×4=68項である。(ただし、実際にはμとνは入れ替えてもイコールとなる対照行列の要素だから、実際にはラムダを固定した時の項4×4=16通りのうち、意味のある値は10通りしかないことに注意したい。)よって、測地線の方程式は、44個の連立方程式をひとまとめに略して書いてあるのである。
ここでクリストッフェル記号Γの中身を説明する。
展開した際の式は以下。
重力場の方程式
一見するとシンプルな式に見えるが、まったくもってそうではない。
まず左辺の

から見ていく。
この部分は次の2つから構成されている。

右辺第1項の

はリッチ・テンソルと呼ばれるものであり、右辺第2項の

はリッチ・スカラーと呼ばれるものである。
リッチ・スカラーはリッチ・テンソルを縮約してつくられている。

これはアインシュタインの省略法を用いて書いているため、実際には次のようになる。





ただし、この中で意味のある項は10個である。
したがって、リッチ・スカラーはリッチ・テンソルから成り立っている。
リッチ・テンソルはリーマン・テンソルと呼ばれる4階のテンソル

を縮約してつくられている。

かつ

省略法を減らして書くと次のようになる。





となる。
ただし、たとえば

となる。
したがって、リッチ・テンソルはリーマン・テンソルから成り立っている。
リッチ・スカラーとリッチ・テンソルを計算するため、リーマン・テンソルについて説明する。



であり、かつ、τの省略を戻すと、
クリストッフェル記号Γの中身は前の項目で示したものと同じである。
4.リーマン幾何学
初等教育で学ぶユークリッド幾何学は、平らな空間を前提とした幾何学である。
一方リーマン幾何学は、まがった空間の図形を対象とする。
リーマン幾何学は重力場の方程式を理解するうえでは必要だが、このwikiの趣旨は物理学を習得することではないため、ここでは概ね割愛するが、先に共役微分についてだけ説明しておく。
リーマン幾何学では座標が平面でないため、座標の取り方によって、同じベクトルであっても見かけ上変化が生じてしまう。その効果を削除したものは共役微分(ナブラ)である。
重力場の方程式の導出
ここでは、リーマン幾何学の諸知識から、重力場の方程式の正しさを検証していくことにする。
ニュートン力学ではエネルギーの源は「質量密度ρ(質量)」だった。しかし、質量密度には運動量密度などが存在しない。そこで相対性理論では、重力場の源は「エネルギー運動量テンソル」だという新しい考えに立つことにする。
そこで、式の右辺には2階の反変テンソルであるエネルギー運動量テンソル

を置く。このとき、左辺も同じ形式のテンソルになるため、仮にこの道の2階の反変テンソルを

とする。

ところで、エネルギー運動量テンソルが偏微分において次の関係を満たしていることを前に証明した。

これはエネルギー保存、運動量保存の式である。しかし、これは平らな空間であるユークリッド幾何学でのみ成り立つ関係式である。今はリーマン幾何学を考えているため、共役微分におけるナブラの関係を考えると以下のように拡張できる。

すると、左辺の

を共変微分したものもまた同じように0にならなければならに。

このような性質を満たした量

が、アインシュタインテンソル(逆トレースリッチテンソル)

である。しかし、
しかし、アインシュタインテンソルとエネルギー運動量テンソルは次元が合わないため、係数kを与えて次の等式が成り立つようにする。

以上が重力場の方程式の簡潔な導入である。
5.ロバートソン・ウォーカー計量
曲がった1次元の世界
まず、曲がった1次元の世界を考える。
この世界は円であるため、

で表される。
極座標が表すと、$$x=R\cos\theta, $y=R\sin\theta$$となる。
ところで、「曲がっていない2次元の世界」つまり「真っ平らな世界」では、わずかに離れた2点間の距離はデカルト座標を使って次のようにあらわされる。

これを極座標であらわすためには、Rやθが変化したとき、dxとdyがそれぞれどれだけ変化するのか計算すればよい。すなわち、Rとθで偏微分すればよい。


これらを代入すれば、dR, dθだけ移動したときの距離が求められる。

これらが「平らな2次元」の上に極座標を引いたときの計量である。しかし「曲がっている1次元」の世界ではRは変化しないので次のようになる。

…*1
しかし、これでは角変数θが現れ、1次元で扱うのは難しい。
そこで2次元から見た場合、lによってθを次のように表せることがわかる。

計算すると、

となる。
これを*1式に当てはめると次のようになる。

曲がった2次元の世界
次に、曲がった2次元の世界を考える。
この世界は球であるため、

で表される。
極座標が表すと、

となる。
ところで、「曲がっていない3次元の世界」では、わずかに離れた2点間の距離はデカルト座標を使って次のようにあらわされる。

これを極座標であらわすためには、Rやθやφが変化したとき、dxとdyがそれぞれどれだけ変化するのか計算すればよい。すなわち、Rとθとφで偏微分すればよい。
それらの結果を代入すれば、dR, dθ, dφだけ移動したときの距離が求められる。

これらが「曲がっていない3次元」の上に極座標を引いたときの計量である。しかし「曲がっている2次元」の世界ではRは変化しないので次のようになる。

…*2
しかし、これでは角変数が(θ、φ)の2つとなり、2次元で扱うのは難しい。
そこで3次元から見た場合、ρによってθを次のように表せることがわかる。

今、

なので、計算すると、

となる。
これを*2式に当てはめると次のようになる。

さらに単純化するため、曲率

を導入すると、次のようになる。

曲がった3次元の世界
次に、曲がった2次元の世界を考える。
今までと違って、この世界の形がわからないが、4次元空間なので

で表される。
これについて、帰納的に次のような極座標を想定できる。




ところで、「曲がっていない4次元の世界」では、わずかに離れた2点間の距離はデカルト座標を使って次のようにあらわされる。

これを極座標であらわすためには、Rやθやφやψが変化したとき、dxとdyがそれぞれどれだけ変化するのか計算すればよい。すなわち、Rとθとφとψで偏微分すればよい。
それらの結果を代入すれば、dR, dθ, dφ, dψだけ移動したときの距離が求められる。

これらが「曲がっていない4次元」の上に極座標を引いたときの計量である。しかし「曲がっている3次元」の世界ではRは変化しないので次のようになる。

…*3
これが必要としていた「球形に曲がった3次元」の計量なのである。
しかし、これでは角変数が(ψ、θ、φ)の3つとなり、3次元で扱うのは難しい。
4次元から見ることはできないが、帰納的かつ推論的に考えると、恐らくRによってψを次のように表せると考えられる。

これを使って*3式に当てはめると次のようになる。

さらに単純化するため、rが小さいときに

の近似により次の式が成り立つ。

rを表すために新しい動径ρを用いて

とあらわすとすると、次のようになる。

これを*3式と比べると、

であればよいことになる。
今、

なので、「曲がっている2次元」の時と同様に計算していくと、曲率

を導入して、次のようになる。

時間軸を含めた4次元の世界
さらに時間軸との関係を考えていく。そもそもこの議論は、宇宙のすべての場所は一様であるとの仮定から始めたので、場所によって時間との関係が変わってはならない。しかし、時間によって場所が変化することを禁止しているわけではない。そこで、今までの計算の結果から、次のような形が考えられる。(a(w)はスケール因子(膨張因子)と呼ばれる量で、時刻wでの宇宙の大きさを相対的に示す量。)
![ds^2=-dw^2+a(w)^2\bigl[ \frac{1}{1-K\rho^2}d\rho^2+\rho^2d\theta^2+\rho^2\sin^2\theta d\phi^2 \bigr]](http://chart.apis.google.com/chart?cht=tx&chf=bg,s,ffffff00&chco=000000ff&chs=25&chl=ds%5E2%3D-dw%5E2%2Ba%28w%29%5E2%5Cbigl%5B%20%5Cfrac%7B1%7D%7B1-K%5Crho%5E2%7Dd%5Crho%5E2%2B%5Crho%5E2d%5Ctheta%5E2%2B%5Crho%5E2%5Csin%5E2%5Ctheta%20d%5Cphi%5E2%20%5Cbigr%5D)
これが探し求めていた「ロバートソン・ウォーカー計量」と呼ばれるものである。これが意味するところは、「宇宙が全体としてはおおよそ均等である」という条件を満たす計量である。
これを重力場の方程式に当てはめて解を導き出す。重力場の方程式はこのような形である。

、ただし

念のために宇宙項を加えると、次のようになる。

まず、ロバートソン・ウォーカー計量の式から、計量テンソルは次のようになる。
これを使って計算した結果、次の4成分のみが残る。
まだ長い計算過程があるが、計算することが目的ではないので最終結果を示す。
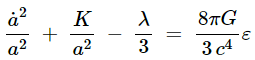
…①
これが、我々が追い求めていたフリードマン方程式である。
また、次の式が、一般相対論におけるエネルギー保存則で、これも導かれる。
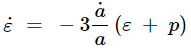
…②
.フリードマン方程式
いよいよ本論である。いままでの全ての解説はこれを説明するための前座であった。
フリードマン方程式やエネルギー保存則で見られるドットは、時間wによる微分を意味しており、w=ctである。
この2つの方程式にはrつの変数ε(=ρ)、p、a、λが含まれている。方程式は2つしかないので方程式として解を出すのは不可能である。そこで、様々な場合が想定されることになる。なお、εは状態方程式(圧力pと密度εの関係)を、Kは宇宙の曲率を、a=a(w)はスケール因子を、λは宇宙項を意味している。
しかし、フリードマンがこの方程式を見つけたとき、宇宙項はまだ存在しなかった。そこで今、λ=0として計算してみる。
このとき、宇宙の速度と加速度は次のようにあらわされる。
したがって、宇宙が速度を下げながらも膨張拡大していることが示された。
なお、この解が発見されたのは1922年であるが、アインシュタインは宇宙は永遠に変化しないと考えていたため、1917年の時点で、重力場方程式に宇宙項Λを入れている。これは、万物がもく万有引力の力に対して斥力に働く宇宙項を採用し、これにより宇宙を定常状態に導くためだったと言われている。
ビッグ・バン
ベルギーの司祭で天文学者のジョルジュ・ルメートルは、ロバートソン・ウォーカー計量に従う方程式を独自に導きだし、渦巻銀河が後退しているという観測結果に基づいて、「宇宙は原始的原子 (primeval atom) の“爆発”から始まった」というモデルを提唱した。
エドウィン・ハッブルの観測結果
さらに、最終的には1929年にエドウィン・ハッブルが宇宙が膨張していることを発見した。アインシュタインはこれを確かめると、人生最大の失敗だと述べて宇宙項を消した。
リンク
最終更新:2017年07月09日 21:39












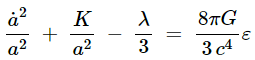 …①
…①
